|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Статистика интервальных данных
Необходимость учета погрешностей измерений. Положим
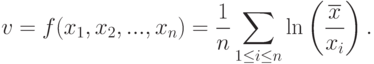
 следует [
[
12.12
]
, с.14], что при малых
следует [
[
12.12
]
, с.14], что при малых 
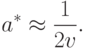 |
( 13) |
В силу состоятельности оценки максимального правдоподобия  из формулы (13) следует, что
из формулы (13) следует, что 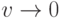 по вероятности при
по вероятности при  .
.
Согласно модели статистики интервальных данных результатами наблюдений являются не  , а
, а  , вместо
, вместо  по реальным данным рассчитывают
по реальным данным рассчитывают
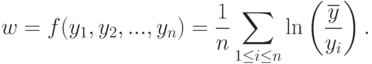
Имеем
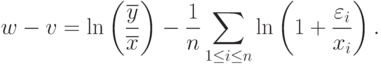 |
( 14) |
В силу закона больших чисел при достаточно малой погрешности  , обеспечивающей возможность приближения
, обеспечивающей возможность приближения 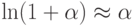 для слагаемых в формуле (14), или, что эквивалентно, при достаточно малых предельной абсолютной погрешности
для слагаемых в формуле (14), или, что эквивалентно, при достаточно малых предельной абсолютной погрешности  в формуле (1) или достаточно малой предельной относительной погрешности
в формуле (1) или достаточно малой предельной относительной погрешности  имеем при
имеем при 
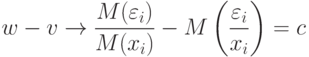
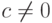 , то оценка максимального правдоподобия не является состоятельной. Имеем
, то оценка максимального правдоподобия не является состоятельной. Имеем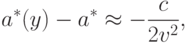
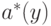 определена по формуле (12) с заменой
определена по формуле (12) с заменой  на
на 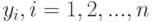 . Из формулы (13) следует [
[
12.12
]
], что
. Из формулы (13) следует [
[
12.12
]
], что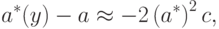 |
( 15) |
 .
.Из формул для  и
и  следует, что с точностью до бесконечно малых более высокого порядка
следует, что с точностью до бесконечно малых более высокого порядка
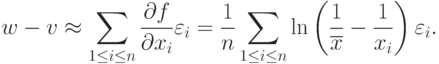 |
( 16) |
С целью нахождения асимптотического распределения  выделим, используя формулу (16) и формулу для
выделим, используя формулу (16) и формулу для  , главные члены в соответствующих слагаемых
, главные члены в соответствующих слагаемых
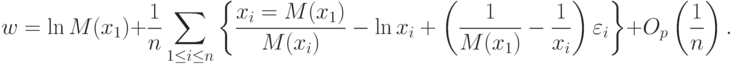 |
( 17) |
Таким образом, величина w представлена в виде суммы независимых одинаково распределенных случайных величин (с точностью до зависящего от случая остаточного члена порядка 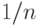 ). В каждом слагаемом выделяются две части - одна, соответствующая
). В каждом слагаемом выделяются две части - одна, соответствующая  , и вторая, в которую входят
, и вторая, в которую входят 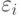 . На основе представления (17) можно показать, что при
. На основе представления (17) можно показать, что при 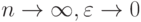 распределения случайных величин
распределения случайных величин  и
и  асимптотически нормальны, причем
M(w)\approx M(v)+c,
D(w)\approx D(v).
асимптотически нормальны, причем
M(w)\approx M(v)+c,
D(w)\approx D(v).
Из асимптотического совпадения дисперсий  и
и  , вида параметров асимптотического распределения (при
, вида параметров асимптотического распределения (при  ) оценки максимального правдоподобия
) оценки максимального правдоподобия  и формулы (15) вытекает одно из основных соотношений статистики интервальных данных о квадрате средней ошибки
и формулы (15) вытекает одно из основных соотношений статистики интервальных данных о квадрате средней ошибки
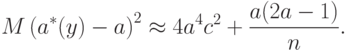 |
( 18) |
Соотношение (18) уточняет утверждение о несостоятельности  . Из него следует также, что не имеет смысла безгранично увеличивать объем выборки
. Из него следует также, что не имеет смысла безгранично увеличивать объем выборки  с целью повышения точности оценивания параметра
с целью повышения точности оценивания параметра  , поскольку при этом уменьшается только второе слагаемое в (18), а первое остается постоянным.
, поскольку при этом уменьшается только второе слагаемое в (18), а первое остается постоянным.
В соответствии с общим подходом статистики интервальных данных в стандарте [ [ 12.12 ] ] предлагается определять рациональный объем выборки nrat из условия "уравнивания погрешностей" (это условие было впервые предложено в монографии [ [ 1.15 ] ]) различных видов в формуле (18), т.е. из условия
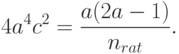
Упрощая это уравнение в предположении  , получаем, что
, получаем, что

Согласно сказанному выше, целесообразно использовать лишь выборки с объемами 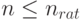 . Превышение рационального объема выборки
. Превышение рационального объема выборки 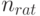 не дает существенного повышения точности оценивания.
не дает существенного повышения точности оценивания.
Применение методов теории устойчивости. Найдем асимптотическую нотну. Как следует из вида главного линейного члена в формуле (17), решение оптимизационной задачи
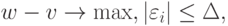
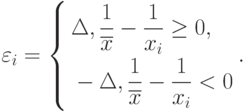
Однако при этом пары 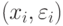 не образуют простую случайную выборку, так как в выражения для
не образуют простую случайную выборку, так как в выражения для 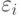 входит
входит  . Однако при
. Однако при  можно заменить
можно заменить  на
на 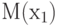 . Тогда получаем, что
. Тогда получаем, что
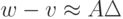
 , где
, где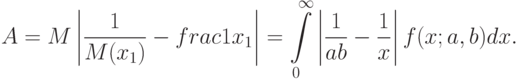
Таким образом, с точностью до бесконечно малых более высокого порядка нотна имеет вид
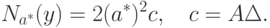
Применим полученные результаты к построению доверительных интервалов. В постановке классической математической статистики (т.е. при 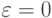 ) асимптотический (при
) асимптотический (при  ) доверительный интервал для параметра формы
) доверительный интервал для параметра формы  , соответствующий доверительной вероятности , имеет вид [
[
12.12
]
]:
, соответствующий доверительной вероятности , имеет вид [
[
12.12
]
]:
![\left[
a^*-u\left(\frac{1+\gamma}{2}\right)\sigma^*(a^*);
a^*+u\left(\frac{1+\gamma}{2}\right)\sigma^*(a^*)
\right],](/sites/default/files/tex_cache/d277dfdfedc9f2097f124ebd8d5504ac.png)
 - квантиль порядка
- квантиль порядка 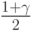 стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1,
стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1,![[\sigma^*(x^*)]^2=
\frac{a}{n(a^*\psi'(x^*)-1)},
\psi(a)=\left.\frac{d\Gamma(a)}{da}right/\Gamma(a).](/sites/default/files/tex_cache/51026e236606c51fe9d26cff18fa9c10.png)
В постановке статистики интервальных данных (т.е. при  ) следует рассматривать доверительный интервал
) следует рассматривать доверительный интервал
![\left[
a^*-2(a^*)^2|c|-u\left(\frac{1+\gamma}{2}\right)\sigma^*(a^*);
a^*+2(a^*)^2|c|-u\left(\frac{1+\gamma}{2}\right)\sigma^*(a^*)
\right],](/sites/default/files/tex_cache/d4d6c252f2f868edbef92044e52dfdca.png)
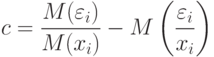
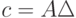 в оптимизационной постановке. Как в вероятностной, так и в оптимизационной постановках длина доверительного интервала не стремится к 0 при
в оптимизационной постановке. Как в вероятностной, так и в оптимизационной постановках длина доверительного интервала не стремится к 0 при  .
.Если ограничения наложены на предельную относительную погрешность, задана величина  , то значение с можно найти с помощью следующих правил приближенных вычислений [
[
12.4
]
, с.142].
, то значение с можно найти с помощью следующих правил приближенных вычислений [
[
12.4
]
, с.142].
(I)Относительная погрешность суммы заключена между наибольшей и наименьшей из относительных погрешностей слагаемых.
(II) Относительная погрешность произведения и частного равна сумме относительных погрешностей сомножителей или, соответственно, делимого и делителя.
Можно показать, что в рамках статистики интервальных данных с ограничениями на относительную погрешность правила (I) и (II) являются строгими утверждениями при 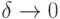 .
.
Обозначим относительную погрешность некоторой величины  через
через  , абсолютную погрешность - через
, абсолютную погрешность - через 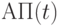 .
.
Из правила (I) следует, что 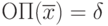 , а из правила (II) - что
, а из правила (II) - что
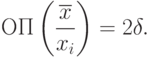
Поскольку рассмотрения ведутся при  то в силу неравенства Чебышева
то в силу неравенства Чебышева
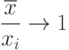 |
( 19) |
 поскольку и числитель, и знаменатель в (19) с близкой к 1 вероятностью лежат в промежутке
поскольку и числитель, и знаменатель в (19) с близкой к 1 вероятностью лежат в промежутке ![[ab-db\sqrt{a};ab+db\sqrt{a}]](/sites/default/files/tex_cache/ece069255497bd4687f6dcd1d6f01045.png) , где константа
, где константа  может быть определена с помощью упомянутого неравенства Чебышева.
может быть определена с помощью упомянутого неравенства Чебышева.Поскольку при справедливости (19) с точностью до бесконечно малых более высокого порядка
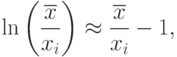
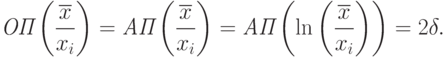 |
( 20) |
Применим еще одно правило приближенных вычислений [ [ 12.4 ] , с.142].
(III) Предельная абсолютная погрешность суммы равна сумме предельных абсолютных погрешностей слагаемых.
Из (20) и правила (III) следует, что 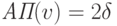 .
.
Из (15) и (21) вытекает [
[
12.12
]
, с.44, форм. (18)], что 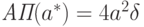 , откуда в соответствии с ранее полученной формулой для рационального объема выборки с заменой
, откуда в соответствии с ранее полученной формулой для рационального объема выборки с заменой 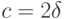 получаем, что
получаем, что
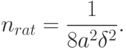
В частности, при 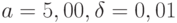 получаем
получаем 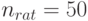 , т.е. в ситуации, в которой были получены данные о наработке резцов до предельного состояния [
[
12.12
]
, с.29], проводить более 50 наблюдений нерационально.
, т.е. в ситуации, в которой были получены данные о наработке резцов до предельного состояния [
[
12.12
]
, с.29], проводить более 50 наблюдений нерационально.
В соответствии с ранее проведенными рассмотрениями асимптотический доверительный интервал для a, соответствующий доверительной вероятности  , имеет вид
, имеет вид
![\left[
a^*-4(a^*)^2\delta-1,96\sqrt{\frac{a^*(2a^*-1)}{n}};
a^*+4(a^*)^2\delta-1,96\sqrt{\frac{a^*(2a^*-1)}{n}}
\right].](/sites/default/files/tex_cache/52a50c0f3f652a735015daca34164299.png)
В частности, при  имеем асимптотический доверительный интервал
имеем асимптотический доверительный интервал ![[2,12; 7,86]](/sites/default/files/tex_cache/7e0f49b6433c3ff4f32f5d5896fbdc5e.png) вместо
вместо ![[3,14; 6,86]](/sites/default/files/tex_cache/f1687ca117f9639165be5d3fdf8f0a6c.png) при
при 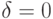 .
.
При больших  в силу соображений, приведенных при выводе формулы (19), можно связать между собой относительную и абсолютную погрешности результатов наблюдений
в силу соображений, приведенных при выводе формулы (19), можно связать между собой относительную и абсолютную погрешности результатов наблюдений  :
:
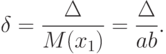 |
( 21) |
Следовательно, при больших  имеем
имеем
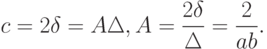
Таким образом, проведенные рассуждения дали возможность вычислить асимптотику интеграла, задающего величину  .
.
Сравнение методов оценивания. Изучим влияние погрешностей измерений (с ограничениями на абсолютную погрешность) на оценку  метода моментов. Имеем
метода моментов. Имеем 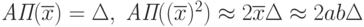 .
.
Погрешность 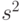 зависит от способа вычисления
зависит от способа вычисления 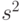 . Если используется формула
. Если используется формула
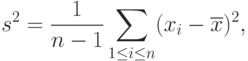 |
( 22) |
![\textit{АП}(x_i-\overline{x})^2=2\Delta,
\textit{АП}\left[(x_i-\overline{x})^2\right]\approx 2|x_i-\overline{x}|\Delta.](/sites/default/files/tex_cache/f061a200213ac18689d9d75d265537ca.png)
По сравнению с анализом влияния погрешностей на оценку 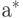 здесь возникает новый момент - необходимость учета погрешностей в случайной составляющей отклонения оценки
здесь возникает новый момент - необходимость учета погрешностей в случайной составляющей отклонения оценки  от оцениваемого параметра, в то время как при рассмотрении оценки максимального правдоподобия погрешности давали лишь смещение. Примем в соответствии с неравенством Чебышева
от оцениваемого параметра, в то время как при рассмотрении оценки максимального правдоподобия погрешности давали лишь смещение. Примем в соответствии с неравенством Чебышева
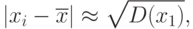 |
( 23) |
![\textit{АП}[(x_i-\overline{x})^2]\approx 2b\sqrt{a}\Delta,\;
\textit{АП}(s^2)\approx 2b\sqrt{a}\Delta.](/sites/default/files/tex_cache/69c26bb13b4fe8dee585e8f0c6814006.png)
 |
( 24) |
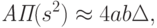
Из полученных результатов следует, что
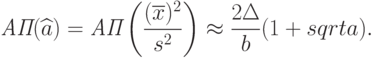

Эта формула отличается от приведенной в [ [ 12.12 ] , с.44, форм. (19)]

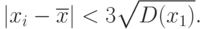
Используя соотношение (23), мы характеризуем влияние погрешностей "в среднем".
Доверительный интервал, соответствующий доверительной вероятности 0,95, имеет вид \left[ \widehat{a}-2\widehat{a}(1+\sqrt{\widehat{a}})\delta-1,96\sqrt{\frac{2\widehat{a}(\widehat{a}+1)}{n}}; \widehat{a}+2\widehat{a}(1+\sqrt{\widehat{a}})\delta+1,96\sqrt{\frac{2\widehat{a}(\widehat{a}+1)}{n}} \right].
Если  , то получаем доверительный интервал
, то получаем доверительный интервал ![[2,54; 7,46]](/sites/default/files/tex_cache/a3a3c0ae52c31810eaabf4c0e2480705.png) вместо
вместо ![[2,86; 7,14]](/sites/default/files/tex_cache/e22d1e3b2a7fb7beb76b43b36dd1ac84.png) при
при 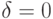 . Хотя при
. Хотя при 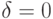 доверительный интервал для
доверительный интервал для  при использовании оценки метода моментов
при использовании оценки метода моментов  шире, чем при использовании оценки максимального правдоподобия
шире, чем при использовании оценки максимального правдоподобия 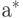 , при
, при 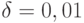 результат сравнения длин интервалов противоположен.
результат сравнения длин интервалов противоположен.
Необходимо выбрать способ сравнения двух методов оценивания параметра  , поскольку в длины доверительных интервалов входят две составляющие - зависящая от доверительной вероятности и не зависящая от нее. Выберем
, поскольку в длины доверительных интервалов входят две составляющие - зависящая от доверительной вероятности и не зависящая от нее. Выберем 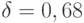 , т.е.
, т.е. 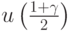 . Тогда оценке максимального правдоподобия
. Тогда оценке максимального правдоподобия  соответствует полудлина доверительного интервала
соответствует полудлина доверительного интервала
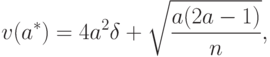 |
( 25) |
 метода моментов соответствует полудлина доверительного интервала
метода моментов соответствует полудлина доверительного интервала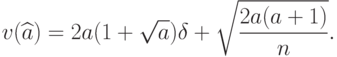 |
( 26) |
Ясно, что больших  или больших
или больших  справедливо неравенство
справедливо неравенство 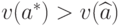 , т.е. метод моментов лучше метода максимального правдоподобия, вопреки классическим результатам Р.Фишера при
, т.е. метод моментов лучше метода максимального правдоподобия, вопреки классическим результатам Р.Фишера при 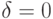 [
[
1.7
]
,с.99].
[
[
1.7
]
,с.99].
Из (25) и (26) элементарными преобразованиями получаем следующее правило принятия решений. Если
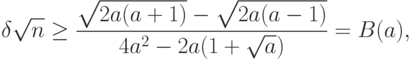
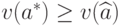 и следует использовать
и следует использовать  ; а если
; а если 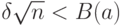 , то
, то 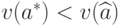 и надо применять
и надо применять 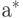 . Для выбора метода оценивания при обработке реальных данных целесообразно использовать
. Для выбора метода оценивания при обработке реальных данных целесообразно использовать 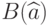 (см. раздел 5 в ГОСТ 11.011-83 [
[
12.12
]
, с.10-11]).
(см. раздел 5 в ГОСТ 11.011-83 [
[
12.12
]
, с.10-11]).Пример анализа реальных данных опубликован в [ [ 12.12 ] ].
На основе рассмотрения проблем оценивания параметров гамма-распределения можно сделать некоторые общие выводы. Если в классической теории математической статистики:
а) существуют состоятельные оценки 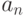 параметра
параметра  ,
,
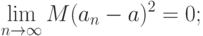
б) для повышения точности оценивания объем выборки целесообразно безгранично увеличивать;
в) оценки максимального правдоподобия лучше оценок метода моментов,
то в статистике интервальных данных, учитывающей погрешности измерений, соответственно:
а) не существует состоятельных оценок: для любой оценки 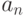 существует константа
существует константа  такая, что
такая, что
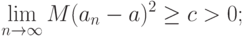
б) не имеет смысла рассматривать объемы выборок, большие "рационального объема выборки" 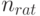 ;
;
в) оценки метода моментов в обширной области параметров 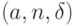 лучше оценок максимального правдоподобия, в частности, при
лучше оценок максимального правдоподобия, в частности, при  и при
и при  .
.
Ясно, что приведенные выше результаты справедливы не только для рассмотренной задачи оценивания параметров гамма-распределения, но и для многих других постановок прикладной математической статистики.
