| Украина |
Кривые и поверхности в компьютерной геометрии, II
Поверхности Лагранжа. Аналогично интерполяционной кривой Лагранжа, можно построить поверхность Лагранжа, затягивающую заданный остов кривых (6.20). Эта поверхность описывается радиус-вектором
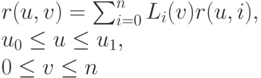
где

Последняя формула получается из формулы для коэффициентов интерполяционного полинома Лагранжа подстановкой 
Поверхность Лагранжа имеет те же недостатки, что и интерполяционный полином Лагранжа - необоснованные изгибы при неравномерном расположении кривых остова в пространстве. По параметру v поверхность будет бесконечно гладкой и представляет собой многочлен. Гладкость по параметру u зависит от гладкости кривых остова.
Поверхности Гордона. Пусть задан остов поверхности, состоящий из двух семейств кривых в обоих параметрических направлениях, которые образуют сетку - т. е. каждая кривая одного семейства пересекает в одной и только одной точке каждую кривую другого семейства. Различные кривые одного и того же семейства не пересекаются. Обозначим заданную таким образом сетку кривых через
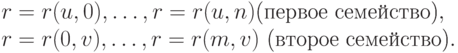 |
( 6.21) |
Здесь  Радиус-вектор точки пересечения j -й кривой первого семейства с i -й кривой второго семейства равен
Радиус-вектор точки пересечения j -й кривой первого семейства с i -й кривой второго семейства равен 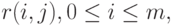
Определение 6.3.3. Поверхностью Гордона, затягивающей сетку кривых (6.21), называется поверхность
 |
( 6.22) |
где
 |
( 6.23) |
- коэффициенты Лагранжа.
Обобщенная поверхность Гордона задается формулой (6.22), в которой вместо коэффициентов Лагранжа (6.23) используются произвольные 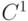 -функции
-функции  которые в целых точках соответствующего промежутка удовлетворяют условию
которые в целых точках соответствующего промежутка удовлетворяют условию

Например, в качестве  можно взять функции смещения (6.19). Гладкость обобщенной поверхности Гордона зависит от гладкости используемых функций
можно взять функции смещения (6.19). Гладкость обобщенной поверхности Гордона зависит от гладкости используемых функций  Поверхности Гордона, построенные по коэффициентам Лагранжа, имеют гладкость
Поверхности Гордона, построенные по коэффициентам Лагранжа, имеют гладкость  но могут образовывать необоснованные изгибы.
но могут образовывать необоснованные изгибы.
Поверхности, затягивающие сетку кривых заплатами Кунса. Остов, состоящий из сетки кривых (6.21), можно затянуть поверхностью, состоящей из заплат, затягивающих каждую отдельную ячейку сетки и гладко сопрягающихся между собой. В качестве таких заплат могут выступать поверхности Кунса. Получается следующая поверхность:
 |
( 6.24) |
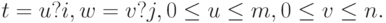 Здесь
Здесь ![i = [u]](/sites/default/files/tex_cache/fa3928efcbdb4207ddf3fffea8eed30b.png) - целая часть
- целая часть ![u, j = [v]](/sites/default/files/tex_cache/d9a91a9f770454ecd3b713106db62cba.png) - целая часть
- целая часть  - дробная часть
- дробная часть  - дробная часть
- дробная часть  - местные параметры в данной ячейке сетки (6.21). Согласно (6.21), области изменения параметров u и v таковы:
- местные параметры в данной ячейке сетки (6.21). Согласно (6.21), области изменения параметров u и v таковы: 
Для вычисления радиус-вектора поверхности с помощью формулы (6.24) необходимо задать производные на кривых сетки в трансверсальном направлении к этим кривым. По аналогии с кубическими сплайнами Эрмита, это можно сделать, например, по следующим формулам:

при  (т. е. для внутренних линий сетки) и по формулам
(т. е. для внутренних линий сетки) и по формулам
 |
( 6.25) |
для крайних линий сетки.
Геометрически это означает, что производная  в произвольной точке
в произвольной точке 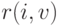 внутренней линии сетки полагается пропорциональной вектору, соединяющему точки
внутренней линии сетки полагается пропорциональной вектору, соединяющему точки  и
и 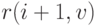 на соседних с ней линиях сетки, отвечающие тому же значению параметра v, что и данная точка. Аналогичное утверждение справедливо и для производной
на соседних с ней линиях сетки, отвечающие тому же значению параметра v, что и данная точка. Аналогичное утверждение справедливо и для производной 
Так же как и в случае кубических сплайнов Эрмита, формулы (6.25) обеспечивают равенство нулю третьих производных поверхности на границе в трансверсальном к граничной кривой направлении.
Поверхности тензорного произведения. Рассмотрим обобщенную поверхность Гордона (6.22), построенную по сетке кривых, которые являются кубическими сплайнами Эрмита. Ясно, что такая поверхность целиком определяется узлами сетки и первыми производными в узлах, заданными в обоих параметрических направлениях (поскольку этими величинами целиком определяются кубические сплайны Эрмита, являющиеся кривыми сетки). Таким образом, в данном случае поверхность строится фактически не по сетке кривых, а по набору точек (узлов) с заданными в них производными. Такие поверхности называются поверхностями тензорного произведения.
Для того чтобы получить формулу поверхности тензорного произведения, поставим в формулу (6.22) выражения, определяющие кубические сплайны Эрмита (линии сетки) и их производные по u и v:
 |
( 6.26) |
где, напомним:

где ![x \in [0,1]](/sites/default/files/tex_cache/f955f8d07e243b2dcff7ca9d2aee424c.png) - местный параметр. В формулах (6.26) через
- местный параметр. В формулах (6.26) через 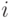 и
и  обозначены целые части параметров u и v соответственно. Местные параметры
обозначены целые части параметров u и v соответственно. Местные параметры  и
и  определяются как
определяются как  Вторые две формулы в (6.26) получаются дифференцированием формулы (6.22). После подстановки формул (6.26) в (6.22) и несложных алгебраических преобразований получим следующее выражение для радиус-вектора поверхности тензорного произведения (в матричных обозначениях):
Вторые две формулы в (6.26) получаются дифференцированием формулы (6.22). После подстановки формул (6.26) в (6.22) и несложных алгебраических преобразований получим следующее выражение для радиус-вектора поверхности тензорного произведения (в матричных обозначениях):
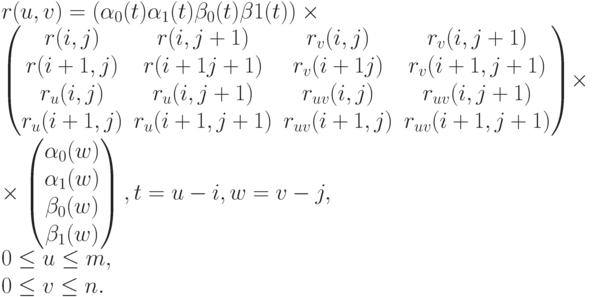 |
( 6.27) |
Из формулы (6.27) хорошо видно, что поверхность тензорного произведения определяется величинами, заданными лишь в узлах сетки.
Поверхности с треугольной параметрической областью
При триангуляции поверхностей иногда бывает удобно рассматривать криволинейные поверхности треугольной формы, имеющие в качестве параметрической области треугольник на плоскости. При этом удобно пользоваться не декартовыми, а барицентрическими параметрическими координатами.
Барицентрические координаты
Лемма 6.6. Пусть даны три точки  не лежащие на одной прямой. Тогда для любой точки
не лежащие на одной прямой. Тогда для любой точки  существует единственная тройка чисел
существует единственная тройка чисел  таких, что
таких, что

Здесь через  обозначены радиус-векторы точек
обозначены радиус-векторы точек  соответственно.
соответственно.
Числа 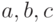 называются барицентрическими координатами точки P относительно треугольника
называются барицентрическими координатами точки P относительно треугольника 
Следствие 6.5. Имеют место формулы

т. е. коэффициенты 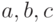 по модулю равны отношению площади треугольника
по модулю равны отношению площади треугольника  в котором соответствующая вершина заменена на
в котором соответствующая вершина заменена на  к площади исходного треугольника
к площади исходного треугольника 
Следствие 6.6. Все три барицентрические координаты точки положительны тогда и только тогда, когда точка принадлежит внутренности треугольника  Все три барицентрические координаты точки неотрицательны тогда и только тогда, когда точка принадлежит треугольнику
Все три барицентрические координаты точки неотрицательны тогда и только тогда, когда точка принадлежит треугольнику 
Билинейная треугольная поверхность. Пусть даны три точки  в
в  В качестве области параметров возьмем треугольник
В качестве области параметров возьмем треугольник  Точка параметрического пространства описывается координатами
Точка параметрического пространства описывается координатами 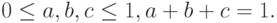 Радиус-вектор треугольной поверхности с вершинами в точках
Радиус-вектор треугольной поверхности с вершинами в точках  задается формулой
задается формулой  где
где  -радиус-вектор точки
-радиус-вектор точки 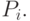
Треугольная поверхность на трех кривых. Пусть даны три попарно пересекающиеся кривые  пересекающиеся в точках
пересекающиеся в точках  Определим треугольную поверхность формулой
Определим треугольную поверхность формулой
 |
( 6.28) |
где  Легко проверить, что при
Легко проверить, что при 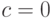 формула (6.28) описывает кривую
формула (6.28) описывает кривую  при
при 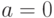 - кривую
- кривую  при
при  - кривую
- кривую  Например, если
Например, если  то
то  и, согласно (6.28), имеем
и, согласно (6.28), имеем

Пример 6.3.5. Поверхность, соединяющая три поверхности по кривым на их границах. При изменении поверхностей, имеющих вид "треугольника", построенная поверхность не изменяется:
In[23]: =
DynamicModule[{pe200, pe002, pel0l, te, tee, pe020, pell0, pe0ll, r2 , rf2 ,
rf1, u, v, w, s, t, рb020, рb002, pb0ll, tb, tbb, pb200, pbl0l, pbll0, rl,
pj200, pj020, pjll0, tj , tjj, pj002, pjl0l, pj0ll, гЗ, rf3, flperem, f2perem,
f3perem, rfel},
pe200 = {0, 10, 0} ; pe002 = {10, 0, 0} ; pel01 = {10, 10, 0}; pb020 = {0, 0, 20};
pb002 = {10, 0, 0} ; pb0ll = {10, 0, 20} ; pj200 = {0, 10, 0}; pj020 = {0, 0, 20};
pjll0 = {0, 10, 20} ;
pe020[te_] := If [te <= 0.5, {8,8,10}+2 tee ({20, 20, 0}-{8, 8, 10}) /. tee -> te,
{20, 20, 0} + 2 {tee- 0.5) ({8, 8, -10} - {20, 20, 0}) / . tee -> te] ;
pell0[te_] := If [te <= 0.5, {4, 9, 5}+2 tee ({10, 15, 0} - {4, 9, 5}) /. tee -> te,
{10, 15, 0} + 2 {tee- 0.5) ({4, 9, -5} - {10, 15, 0}) /. tee -> te] ;
pe011[te_] :=If[te <= 0.5, {9, 4, 5} + 2 tee ({15, 10, 0} - {9, 4, 5}) /. tee -> te,
{15, 10, 0} + 2 (tee- 0.5) ({9, 4, -5} - {15, 10, 0}) /. tee -> te] ;
r2 [ te_] : = pe200 u u + pe020 [ te] v v + pe002 w w + 2 pel0l u w + 2 pel 10 [ te] u v +
2 pe011[te] vw;
rf2[ te_, s_, t_] := r2 [te] /.w ->l-u-v/. {u -> t- s t, v-> s t} ;
f2perem = ParametricPlot3D[Evaluate[r2 [te] /. w -> l-u-v/. v->0], {u, 0, 1},
Mesh-> 18, PlotStyle -> {Red, AbsoluteThickness [2] } ] ;
pb020 = {0, 0, 20} ; pb002 = {10, 0, 0} ; pb0ll = {10, 0, 20};
pb200 [ tb_] :=If[tb<=0.5, {8, 6, 16}+2 tbb ({20, 0, 40}-{8, 6, 16}) /. tbb -> tb,
{20, 0, 40} + 2 (tbb- 0.5) ({8, -6, 16} - {20, 0, 40}) /. tbb -> tb] ;
pbl01[tb_] := If [tb<= 0.5, {9,3, 8} + 2 tbb ({15, 0, 20} - {9, 3, 8}) /. tbb -> tb,
{15, 0, 20} + 2 (tbb- 0.5) ({9, -3, 8} - {15, 0, 20}) / . tbb -> tb] ;
pbll0[tb_] := If [tb <= 0.5, {4, 3, 18}+2 tbb ({10, 0, 30}-{4, 3, 18}) /. tbb -> tb,
{10, 0, 30} + 2 (tbb- 0.5) ({4, -3, 18} - {10, 0, 30}) / . tbb -> tb] ;
rl [ tb_] : = pb200 [ tb] u u + pb020 v v + pb002 w w + 2 pbl0l [ tb] uw + 2 pbll0 [ tb] u v +
2 pb0ll vw;
rfl [ tb_, s_, t_] := rl [tb] /.w->l-u-v/. {u -> t- s t, v-> s t} ;
flperem = ParametricPlot3D [Evaluate [rl [tb] /. w -> l - u - v / . u -> 0] , {v, 0, 1},
Mesh -> 18, PlotStyle -> {Red, AbsoluteThickness[2]}];
pj200 = {0, 10, 0} ; pj020 = {0, 0, 20} ; pjll0 = {0 , 10, 20};
pj002[tj_] := If [tj<= 0.5, {6, 8, 16} + 2 tj j ({0, 20, 40} - {6, 8, 16}) /. tj j -> tj,
{0, 20, 40} + 2 (tj j - 0.5) ({-6, 8, 16} - {0, 20, 40}) /. tj j -> tj] ;
pjl01[tj_] := If {tj <= 0,5, {5, 9, 3} + 2 tjj ({0, 15, 20}-{5, 9, 8}) /. tj j -> tj,
{0, 15, 20} + 2 (tjj - 0.5) ({-5, 9, 8} - {0, 15, 20}) / . tj j -> tj] ;
pj0ll [tj_] := If [tj <= 0. 5, {5, 4, 18} + 2 tjj ({0, 10, 30}-{5, 4, 18}) /. tjj -> tj,
{0, 10, 30} + 2 (tjj - 0.5) ({-5, 4, 18} - {0, 10, 30}) /. tj j -> tj] ;
r3[ tj_] : = pj200uu+pj020vv + pj002[fcj] v w + 2 pjl0l[tj] u w + 2 pjll0 u v +
2 pj0ll [tj] vw;
rf3[tj_, s_, t_] := r3[tj] /.w->l-u-v/. {u -> t- s t, v-> s t} ;
f3perem = ParametricPlot3D [Evaluate [r3 [tj ] /. w -> 0 / . v->l-u], {u, 0, 1},
Mesh ->18, PlotStyle -> {Red, AbsoluteThickness[2]}];
rfel[tb_, te_, tj_, u_, v_] : =
и (rf3[tj, v, 1] + rf2[te, 0, u + v] - rf2[te, 0, 1] ) +
v (rfl [tb, 1, u+ v] + rf3[tj, 1 - u, 1] - rfl[ tb, 1, 1] ) +
(1-u- v) (rf2[te, 0, u] + rfl[ tb, 1, v] - rf 1 [ tb, 1, 0] ) ; (*три кривые rfl[tb,l,t] ,
rf2[te,0,l-t] и rЈ3[tj,l-t,l] , t Ha [0,1]*)
Manipulate[
Show[{ParametricPlot3D[Evaluate[rfl[tb, s, t] ] , {s, 0, 1}, {t, 0, 1},
Mesh -> None, PlotRange -> All, PlotStyle -> {Opacity [0 . 8] , Green}],
ParametricPlot3D[Evaluate[rf2 [te, s, t] ] , {s, 0, 1}, {t, 0, 1}, Mesh-> None,
PlotRange-> All, PlotStyle -> {Opacity [0 . 9] , Yellow}],
ParametricPlot3D[Evaluate[rf3[tj , s, t] ] , {s, 0, 1}, {t, 0, 1}, Mesh-> None,
PlotRange -> All, PlotStyle-> {Opacity [0 . 8] , Blue}],
ParametricPlot3D[Evaluate[rfel [tb, te, t j , s, t] ] , {s, 0, 1}, {t, 0, 1 - s} ,
Mesh -> {13, 18}, PlotRange-> All] ,
f1perem, f2perem, fЗрегеm} , Viewpoint-> {-0 . 7 , 0.4, 1-3}, ImageSize -> {300 , 200},
Boxed -> False, Axes -> None, PlotRange -> {{-6. , 20.}, {-6., 20.}, {-10., 40.}},
Spherical Region -> True, ViewAngle-> 0 . 7 ],
{{tb, 0.4, "Зеленый ""треугольник '"}, 0., 1., Appearance->'Labeled" } ,
{ {te, 0.4, " Желтый ' ' треугольник '" } , 0 . , 1. , Appearance -> " Labeled" } ,
{ {t j , 0.4, " Синий " " треугольник' ' " } , 0 . , 1. , Appearance -> " Labeled" } ,
SaveDefinitions -> True] ]
