НОУ ИНТУИТ | Практикум по компьютерной геометрии. Лекция 6: Кривые и поверхности в компьютерной геометрии, II

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 27.12.2010 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать программу

B-кривые

Определение 6.1.4. B - кривой порядка m, построенной по вершинам 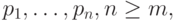$p_1, \dots , p_n, n \ge m,$ с весами 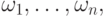$\omega_1, \dots , \omega_n,$ называется кривая

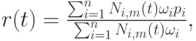
$r(t)=\frac{\sum_{i=1}^n N_{i, m}(t) \omega_ip_i}{\sum_{i=1}^nN_{i, m}(t) \omega_i},$

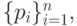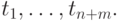
определяемая опорными точками $\{p_i\}_{i=1}^n,$ весами $\{\omega_i\}_{i=1}^n$ и последовательностью узлов $t_1, \dots ,t_{n+m}.$

Определение 6.1.5. Множество узлов $\{t_1, \dots , t_{n+m}\}$ называется расширенным множеством узлов B -кривой.

Замечание 6.1.4.

Управляющими параметрами B -кривой являются:

порядок кривой m,
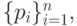
ее опорные точки $\{p_i\}_{i=1}^n,$
веса опорных точек $\{\omega_i\}_{i=1}^n,$
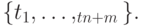
неубывающая последовательность вещественных чисел $\{t_1, \dots , _{tn+m}\}.$

Таким образом, B -кривые обладают дополнительным множеством управляющих параметров по сравнению с рациональными кривыми Безье - расширенным множеством узлов. Именно эти дополнительные параметры и обеспечивают гораздо большую гибкость в управлении B -кривыми, чем кривыми Безье. В современной компьютерной геометрии в основном применяются именно B -кривые.
В отличие от кривых Безье, B -кривые, вообще говоря, не проходят через свои крайние опорные точки. Однако такого прохождения нетрудно добиться с помощью следующего утверждения.

Теорема 6.3. Если первые m узлов расширенного множества совпадают, то B -кривая начинается в своей первой опорной точке 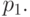p_1. Аналогично, если последние m узлов расширенного множества совпадают, то B -кривая заканчивается в своей последней опорной точке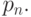 p_n.

B -кривые в пакете Mathematica. Mathematica имеет встроенные функции BSplineFunction и BSplineCurve, которые позволяют строить B -кривые по заданному множеству опорных точек пространства 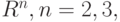R^n, n = 2,3, автоматическим или полуавтоматическим подбором параметров. Расширенное множество узлов по умолчанию подбирается автоматически, однако его можно задать самому с помощью параметра SplineKnots. Например, 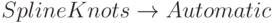$SplineKnots \to Automatic$ означает автоматический подбор расширенного множества узлов, а 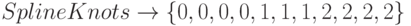$SplineKnots \to \{0, 0, 0, 0, 1, 1, 1, 2, 2, 2, 2\}$ задает расширенное множество узлов непосредственно.

Так же дело обстоит и с весами опорных точек. Веса можно задавать с помощью SplineWeights. Например, 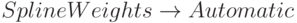$SplineWeights \to Automatic$ означает автоматический выбор весов, а $SplineWeights \to \{1, 1, 10, 1, 1, 1\}$ задает конкретные веса для шести опорных точек.

Порядок сплайнов можно задавать с помощью SplineDegree, но при этом должно быть 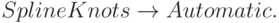$SplineKnots \to Automatic.$

Вычисление порядка происходит так. Число сплайнов в базисе, равное n - m (см. выше), должно равняться числу опорных точек. Поэтому порядок сплайнов может быть вычислен как разность числа узлов и числа опорных точек. Однако для Mathematica эта разность должна быть подобрана так, чтобы она равнялась 4, иначе B -кривая может быть построена в Mathematica неправильно.

Чтобы воспользоваться возможностью полноценного управления B-кривой, в том числе и весов, нужно запрограммировать B -кривую самостоятельно с помощью встроенной функции BSplineBasis.

Задача 6.1.6. С помощью встроенных функций Mathematica SplineFunction и BSplineCurve построить B -кривую по заданным опорным точкам с автоматическим выбором узлов на плоскости и в трехмерном пространстве.

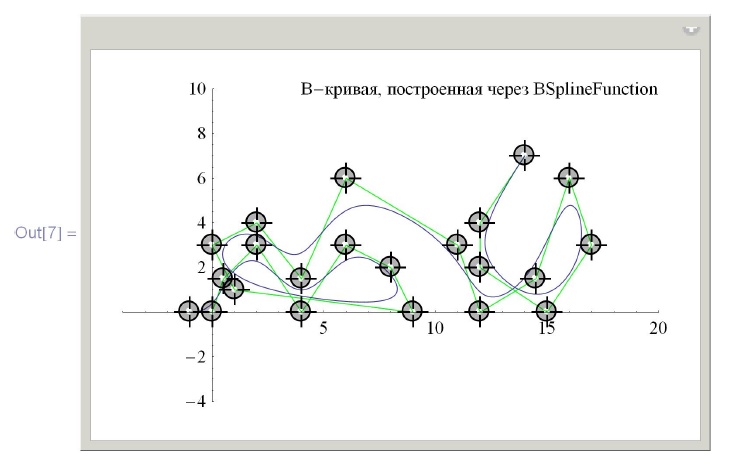
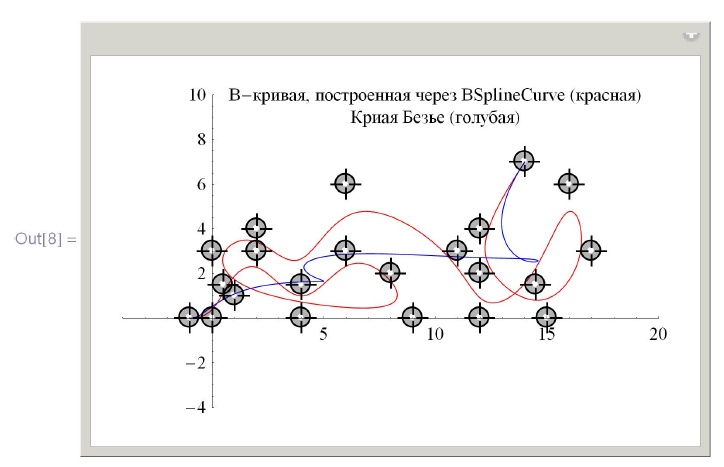
Пример 6.1.4. B -кривая на плоскости с автоматическим выбором узлов, построенная двумя способами: с помощью функций BSplineFunction и BSplineCurve соответственно. На втором графике для сравнения нарисована также простая кривая Безье, построенная по тем же опорным точкам.

In[7] : = DynamicModule [ {ptsO, f, g, n, ptsl, pts2 , t} , 
                   n = Length [ptsO] ;
                Manipulate[f = BSplineFunction[ptsl] ; 
                   Show[{
                     Graphics[{Green, Line[ptsl], Black,
                        Text["B-кривая, построенная через BSplineFunction", {12, 10-0}], 
                        Text[ToString[# - 1] , ptsl [ [#] ] +{0.7, 0}] & /@  Range [n] } , 
                         PlotRange -> {{-4, 20}, {-4, 10}}, Axes -> True] , 
                  ParametricPlot[f[t], {t, 0, 1}]}, ImageSize -> 300] , 
                {{ptsl, pts0}, Locator}], 
            Initialization : -> (
                pts0 = {{-1, 0.0}, {0, 0}, {0.5, 1.5), {2.0, 3.0}, {4, 0}, {6, 3.0}, 
                    {8.0, 2.0}, {9.0, 0}, {1.0, 1.0}, {0.0, 3.0}, {2.0, 4.}, {4.0, 1.5}, 
                    {6.0, 6.0}, {11, 3}, {12.0, 0.0}, {14.5, 1.5}, {16, 6}, {17.0, 3.0}, 
                   {15.0, 0.0}, {12.0, 2.0}, {12.0, 4.0}, {14.0, 7.0}})]

In[8] :=
        DynamicModule [ {ptsO , f, g, n, ptsl, pts2 , t} , 
           n = Length [ptsO] ;
         Manipulate[g = BezierFunction[pts2]; 
            Show [ {
               Graphics [ {Red, BSplineCurve [pts2 , SplineKnots -> Automatic] , Black,
                 Text["В-кривая, построенная через BSplineCurve (красная)", {10, 10.0}],
                 Техt["Криая Беэье (голубая)", {10, 9.0}], 
                       Text [ToSt ring] # - 1] , pts2 [ [#] ] + {0.7, 0}] & /@ Range [n] } , 
                  PlotRange ->  {{-4, 20} , {-4, 10}} , Axes -> True] , 
            ParametricPlot[g[t] , {t, 0, 1}, ElotStyle -> {Blue}] 
          }, ImageSize -> 300] , { {pts2 , pts0}, Locator}], Initialization: -> ( 
           pts0 = {{-1, 0.0}, {0, 0}, {0.5, 1.5}, {2.0, 3.0}, {4, 0}, {6, 3.0}, 
               {8.0, 2.0}, {9.0, 0}, {1.0, 1.0}, {0.0, 3.0}, {2.0, 4.}, {4.0, 1.5}, 
               {6.0, 6.0}, {11, 3}, {12.0, 0.0}, {14.5, 1.5}, {16, 6}, {17.0, 3.0}, 
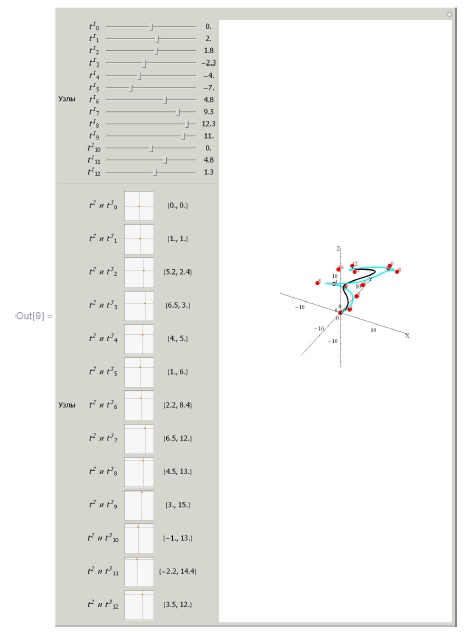
               {15.0, 0.0}, {12.0, 2.0}, {12.0, 4.0}, {14.0, 7.0}})]

Пример 6.1.5. B -кривая в пространстве с автоматическим выбором узлов в сравнении с кривой Безье, построенной по тем же опорным точкам. Обратите внимание, насколько более послушно ведет себя B -кривая при управлении опорными точками, чем кривая Безье. Кривая Безье по-другому - более глобально - усредняет влияние опорных точек на кривую, что делает ее локальное управление за счет смещения отдельных опорных точек гораздо более вязким, чем в случае B -кривой.

In[9]:=
    DynamicModule [ {pts0 , f, pts , n} , 
       Manipulate[f = BezierFunction[pts]; 
         Show[ 
           {Graphics3D[{Cyan, Thick,
              BSplineCurve[pts, SplineKnots -> Automatic], Red,
              PointSize[Large], Point[pts],
             Text[ToString[#- 1] , pts [ [#] ] + {0.4, 0.4, 0.4}] & /@
                Range[n], Black, Text["X", {18, -0.3, -0.3}], 
                  Black, Text["Y", {-0.3, 18, -0.3}], Black, 
                  Text["Z", {-0.3, -0.3, 18}]}, Axes -> True, 
                AxesEdge -> Automatic, AxesOrigin -> {0, 0, 0}], 
              ParametricPlot3D[f[t], {t, 0, 1}, PlotStyle -> {Thick}]}, 
            Boxed -> False,
            PlotRange -> {{-18, 18}, {-18, 18}, {-18, 18}}], 
          {{pts, pts0, "Уэлы"}, 
            With[{r = Range[1, n] } ,
               Grid[{Spacer[3] , Subscript[style["t¹", Italic] , #- l] , 
                   Slider [Dynamic@pts [[#1]] [ [1] ] , {-15, 15, .01}, 
                     Appearance -> "Left", ImageSize -> {200, 12}], 
                   Dynamic@pts[[#1]] [[1]]} & /@ r] ] &, 
           ControlPlacement -> Left} , 
        Delimiter, {{pts, pts0, "Узлы"}, 
          With [ {r = Range [1, n] } , 
            Grid[ 
              {Spacer [3], Subscript [style ["t² и t³", Italic], #-l], 
                   Slider2D [Dynamic® {pts[[1]]  [ [2] ] , pts[[1]] [ [3] ] } , 
                     {{-15, -15}, {15, 15}}, Appearance -> "Left", 
                     ImageSize -> {50, 30}], 
                   Dynamic@ {pts [[#1]] [ [2] ] , pts [[#2]] [[3]]}} & /@ r] ] &, 
                ControlPlacement -> Left}] , 
         Initialization : -> 
            (pts0 = {{0.0, 0.0, 0.0}, {2.0, 1.0, 1.0}, {1.8, 5.2, 2.4}, 
                   {-2.3, 6.5, 3.0}, {-4.0, 4.0, 5.0}, {-7.0, 1.0, 6.0}, 
                  {4.8, 2.2, 8.4}, {9.3, 6.5, 12.0}, {12.3, 4.5, 13.0}, 
                  {11.0, 3.0, 15.0}, {0.0, -1.0, 13.0}, {4.8, -2.2, 14.4}, 
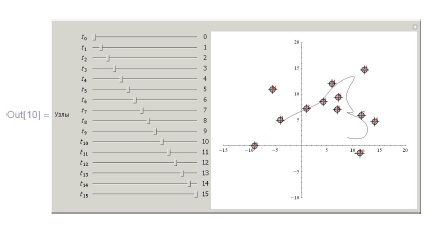
                 {1.3, 3.5, 12.0}}; n = Length[pts0])]

Пример 6.1.6. B -кривая на плоскости с автоматическим выбором порядка, но с управляемыми мышью опорными точками и узлами (узлы должны быть неубывающими).

In[10]:=
        DynamicModule [ {pts0, tt0, n, m, f, tt, i, pts}, 
          pts0 = {{-9.0, 0.0}, {-4.0, 5.0}, {1.1, 7.2}, {4.3, 8.5}, {6.0, 12.0}, 
               {12.1, 14.7}, {7.2, 9.4}, {11.5, 5.9}, {7.0, 7.0}, {14.1, 4.7}, 
             {11.2, -1.4}, {-5.5, 10.9}}; 
          tt0 = Table[i - 1, {i, 1, 16} ] ; n = Length[pts0] , m = Length[tt0] ; 
            Manipulate [f = BSplineCurve [pts , SplineKnots -> tt] ; 
               Show[{If[OrderedQ[tt],
                   Graphics[f, Axes -> True, PlotRange -> {{-15, 20}, {-10, 20}}], 
                   Do [If [tt[[i- 1]] > tt[[i]], tt[[i-1]] = tt[[i]] , {i, 2, m}] ; 
                     Graphics [f , Axes -> True],
               ],
             Graphics[{Red, Point[pts],
                      Text[ToString[# - 1] , pts [[#]] + {0.4, 0.4}] & /@ Range [n] } , 
                  PlotRange -> {{-15, 20} , {-10, 20}}] }] , 
         {{pts, pts0}, Locator}, {{tt, tt0, "Узлы"}, 
            With[{r = Range[l, m] } , 
              Grid[ 
                {Spacer[3] , Subscript [Style ["t" , Italic] , # - 1] ,
                       Slider [Dynamic@tt[[#l]] , {0, 15, .01}, Appearance -> "UpArrow" , 
                          ImageSize -> {200, 12}], Dynamic@tt[[i]]} &/@r]] &, 
             ControlPlacement -> Left}] , Initialization: -> (
             pts0 = {{-9.0, 0.0}, {-4.0, 5.0}, {1.1, 7.2}, {4.3, 8.5}, {6.0, 12.0}, 
                    {12.1, 14.7), {7.2, 9.4}, {11.5, 5.9}, {7.0, 7.0}, {14.1, 4.7}, 
                    {11.2, -1.4}, {-5.5, 10.9}}; 
            tt0 = Table [i - 1, {i, 1, 16} ] ; 
            n = Length[pts0]; 
            m = Length[tt0])]

Пример 6.1.7. B -кривая на плоскости с автоматическим выбором порядка и узлов, но с управляемыми мышью опорными точками и весами, и простая кривая Безье, управляемая теми же опорными точками:

In[11]: =
        DynamicModule [ {pts0, n, w0, f, g, d, curve, w} , 
        pts0 = {{-9.0, 0.0}, {-4.0, 5.0}, {1.1, 7.2}, {4.3, 8.5}, {6.0, 12.0}, 
            {12.1, 14.7}, {10.2, 9.4}, {7.5, 7.9}, {2.0, 4.0}, {1.1, 1.2}, 
            {-17.2, 18.4}, {-16.5, -15.9}}; 
        n = Length [pts0] ; w0 = Table [1, {i , 1, n} ] ; 
        Manipulate[f = BezierFunction[pts] ; 
            g = BSplineCurve [pts , SplineWeights -> w, SplineDegree -> d] ; 
              Show[ 
             Graphics[{Red, Point[pts],
                   Text [To St ring [# - 1] , pts [ [#]]+{0.4,0.4}] & /@ Range [n] } , Axes -> True] , 
                If [curve = = = 1, Graphics [g] , 
                 ParametricPlot[f [t] , {t, 0, 1}, PlotStyle ->  {Red} ] ] ] , 
          {{d, 2, "Степень В-кривой" } , 
              Dynamic@RadioButtonBar [Dynamic [d] , Range[0, 7]] &} , 
          {{curve, 1, "Кривая"} , {1 -> "В-кривая" , 2 -> "Кривая Безье" } } , 
            {{pts, pts0}, Locator}, 
        Delimiter, {{w, w0 , "Узлы"}, 
          With [ {r = Range [1, n] } ,
             Grid[{Spacer[3] , Subscript[Style["w", Italic], # - 1] ,
                      Slider [Dynamic@w[[#1]] , {0, 4, 0.01}, Appearance -> "Left" , 
                         ImageSize ->  {200, 12}], Dynamic @ w[[#1]] } &/@ r] ] &, 
           ControlPlacement -> Left}] , Initialization : -> (
          pts0 = {{-9.0, 0.0}, {-4.0, 5.0}, {1.1, 7.2}, {4.3, 8.5}, {6.0, 12.0}, 
                   {12.1, 14.7}, {10.2, 9.4}, {7.5, 7.9}, {2.0, 4.0}, {1.1, 1.2}, 
                   {-17.2, 18.4}, {-16.5, -15.9}};
          n = Length [pts0] ; w0 = Table[l, {i, l,n}])]

Задача 6.1.7. Самостоятельно запрограммировать B -кривую с помощью встроенной функции BSplineBasis, так, чтобы можно было воспользоваться возможностью полноценного управления B -кривой. Обеспечить возможность произвольного допустимого порядка B -сплайнов.

Дальше >>

Практикум по компьютерной геометрии

Практикум по компьютерной геометрии

Кривые и поверхности в компьютерной геометрии, II

B-кривые

Вопросы и ответы

Студенты

Авторизоваться

Практикум по компьютерной геометрии

Практикум по компьютерной геометрии

Кривые и поверхности в компьютерной геометрии, II

B-кривые

Вопросы и ответы

Студенты