| Украина |
Кривые и поверхности в компьютерной геометрии, II
Алгоритм вычисления радиус-вектора B-кривой
Пусть даны опорные точки 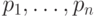 и их веса
и их веса 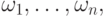 а также расширенное множество неубывающих узлов
а также расширенное множество неубывающих узлов  Опишем алгоритм вычисления радиус-вектора B -кривой
Опишем алгоритм вычисления радиус-вектора B -кривой
-
Фиксируем t. Положим
 Тогда существует единственное
Тогда существует единственное 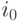 такое, что
такое, что  где
где 
-
Для определенного выше индекса
 если
если  вычисляем единственное ненулевое значение ненормированного B -сплайна первого уровня (m=1):
вычисляем единственное ненулевое значение ненормированного B -сплайна первого уровня (m=1):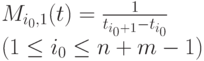
Напомним, что
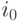 было выбрано на первом шаге, так чтобы
было выбрано на первом шаге, так чтобы  При этом, в силу условия
При этом, в силу условия  знаменатель
знаменатель  а в силу условия
а в силу условия  имеем
имеем 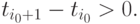 Следовательно,
Следовательно,  Для индекса
Для индекса  находящегося вне множества
находящегося вне множества  значение
значение  не вычисляется.
не вычисляется. -
С помощью соотношений Кокса - де Бура вычисляем все отличные от нуля в точке
 ненормированные сплайны
ненормированные сплайны  -го порядка
-го порядка  при
при 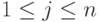 :
:
В частности,
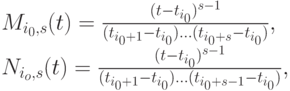
( 6.6) где
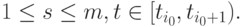 Положив в (6.6)
Положив в (6.6) 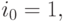 получим
получим
Лемма 6.5. Имеет место соотношение:

-
Вычисляем нормированные сплайны
 для каждого
для каждого 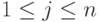 по формуле
по формуле  (при этом
(при этом  ).
). -
Окончательно вычисляем
 по формуле
по формуле
Алгоритм де Бура вычисления радиус-вектора B-кривой
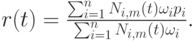
Теорема 6.4. Радиус-вектор r(t) B -кривой:

может быть вычислен с помощью следующего алгоритма:
-
Для заданного
 вычисляем величины
вычисляем величины  при
при 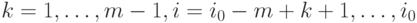 по рекуррентным формулам:
по рекуррентным формулам: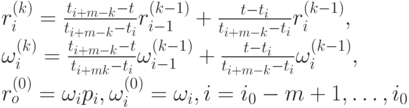
-
Вычисляем r(t) по формуле

Данный алгоритм иллюстрируется следующей диаграммой (  ):
):
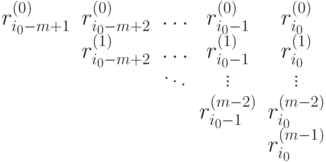
Поверхности, определяемые матрицами опорных точек и весов
Поверхности Безье
Определение 6.2.1. Пусть дано (m +1) * (n+1) точек в пространстве  образующих прямоугольную матрицу (сетку Безье):
образующих прямоугольную матрицу (сетку Безье):
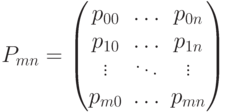
Поверхностью Безье порядка m * n, соответствующей сетке  называется поверхность
называется поверхность
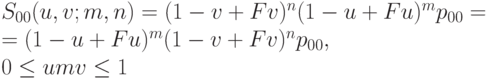 |
( 6.7) |
где E - оператор сдвига вперед по первому индексу, F - оператор сдвига вперед по второму индексу:
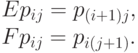
Операторы E и F очевидно коммутируют друг с другом: 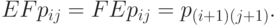 Поэтому
Поэтому 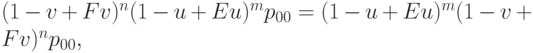 т. е. формула (6.7) непротиворечива.
т. е. формула (6.7) непротиворечива.
Определение 6.2.2. Рациональная поверхность Безье, построенная по точкам 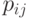 с весами
с весами 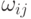 определяется следующим образом:
определяется следующим образом:
 |
( 6.8) |
Формула (6.8) означает, что мы строим поверхность Безье в  по точкам
по точкам 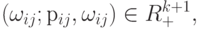 а затем применяем преобразование
а затем применяем преобразование 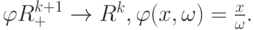
Задача 6.2.1. Наглядно изучить влияние опорных точек и их весов на рациональную поверхность Безье, меняя исходные данные pts (опорные точки) и  (их веса) в нижеследующей программе. В матрице весов стоят двумерные векторы, но используется только их первая компонента. Вторая компонента фиксирована. Это связано с неспособностью Mathematica применять функцию BezierFunction к матрицам из скаляров.
(их веса) в нижеследующей программе. В матрице весов стоят двумерные векторы, но используется только их первая компонента. Вторая компонента фиксирована. Это связано с неспособностью Mathematica применять функцию BezierFunction к матрицам из скаляров.
Пример 6.2.1. Рациональная поверхность Безье с возможностью непосредственного управления весами с помощью движков.
In[12]: =
DynamicModule [ {pts, a, w0, pw, w, g, f, w6, w7, wl0, wll, i, j, out,
ins, u, v, n, pts0},
pts = {{{0, 0, 0}, {0, 1, 0), {0, 2, 0}, {0, 3, 0}},
{{1, 0, 0}, {1, 1, 1}, {1, 2, 1}, {1, 3, 0}},
{{2, 0, 0}, {2, 1, 1}, {2, 2, 1}, {2, 3, 0}},
{{3, 0, 0}, {3, 1, 0}, {3, 2, 0} , {3, 3, 0}}}; pts0 = Flatten [pts, 1] ;
n = Length [pts0] ;
Row[
{Manipulate [w0 = {{{2, a}, {3, a}, {4, a}, {5, a}},
{{3, a}, {w5, a}, {w6, a}, {6, a}}, {{4, a}, {w9, a}, {wl0, a}, {7, a}},
{{9, a}, {12, a}, {14, a}, {32, a}}};
w = Table[w0[ [i, j , 1] ] , {i, 1, 4}, {j, 1, 4}];
pw = Table [w0[ [i, j , 1] ] pts [ [i , j ] ] , {i , 1, 4} , { j , 1, 4} ] ;
g = BezierFunction[w0]; f = BezierFunction[pw];
Show[{Graphics3D[{PointSize[Large], Red, Map[Point, pts] ,
Green, Text[ToString[# - 1] , pts0[[#]] + {0.01, 0.04, 0.04}] & /@
Range[n]}],
Graphics3D[{Gray, Dashed, Line[pts], Line[Transpose[pts]]}],
ParametrioPlot3D[f [u, v] / g [u, v] [ [1] ] , {u, 0, 1}, {v, 0, 1},
PlotStyle -> FaceForm[out, ins] ] }] ,
Column[{Control[{{ins, Green, "Внутренний цвет"}, Green}],
Control[{{out, Red, "Внешний цвет"}, Red}]}, Right],
{{w5, 10}, 1, 100}, {{w6, 10}, 1, 100}, {{w9, 10}, 1, 100},
{{wl0, 10}, 1, 100}]
MatrixForm [pts] } , " " ] ,
Initialization : ->
(pts = {{{0, 0, 0}, {0, 1, 0}, {0, 2, 0}, {0, 3, 0}},
{{1, 0, 0}, {1, 1, 1}, {1, 2, 1}, {1, 3, 0}},
{{2, 0, 0}, {2, 1, 1}, {2, 2, 1}, {2, 3, 0}},
{{3, 0, 0}, {3, 1, 0}, {3, 2, 0}, {3, 3, 0}}}; pts0 = Flatten [pts, 1] ;
a = 1; n = Length[pts0])]Геометрический смысл поверхности Безье
Поверхность Безье можно получить следующим образом:
-
Строим (n + 1) кривую Безье по столбцам матрицы
 :
: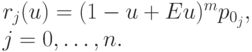
- Далее, начиная с каждой точки кривой Безье
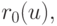 строим кривые Безье, имеющие опорные точки на кривых
строим кривые Безье, имеющие опорные точки на кривых  соответствующие одному и тому же значению параметра u.
соответствующие одному и тому же значению параметра u.
При этом соответствующий оператор перехода от опорной точки, взятой на кривой 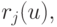 к следующей опорной точке, взятой на кривой
к следующей опорной точке, взятой на кривой 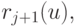 в терминах узлов сетки pij описывается оператором сдвига F по второму индексу. Следовательно,
в терминах узлов сетки pij описывается оператором сдвига F по второму индексу. Следовательно,

где m и n - количество шагов по первому и второму индексу соответственно, начиная от угловой точки сетки Безье, 00 - индекс этой угловой точки, с которой мы начинаем образовывать все остальные узлы сетки операторами сдвига E и F. Имеем
 |
( 6.9) |
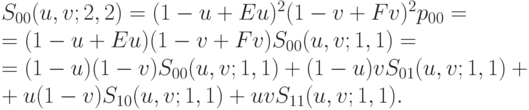 |
( 6.10) |
Здесь через  обозначены четырехугольные листы Безье, построенные из точек p ij, взятых в качестве угловых точек, аналогично формуле (6.9).
обозначены четырехугольные листы Безье, построенные из точек p ij, взятых в качестве угловых точек, аналогично формуле (6.9).
Аналогично формуле (6.10), любая точка на поверхности Безье степени m*n может быть представлена в виде точки четырехугольного листа Безье с углами в точках соответственно подобранных поверхностей Безье порядка (m-1)*(n-1):

Поверхность Безье можно представить в следующим виде:
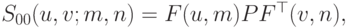
где  и
и

Аналогично обычной поверхности Безье, рациональная поверхность Безье  может быть получена с помощью следующего алгоритма:
может быть получена с помощью следующего алгоритма:
- соединяем
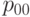 и
и 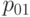 рациональной кривой Безье
рациональной кривой Безье  с весами
с весами  и
и 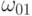 ;
; - соединяем
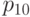 и
и 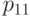 рациональной кривой Безье
рациональной кривой Безье  с весами
с весами 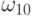
- фиксируем
 соединяем точки
соединяем точки  и
и  с весами
с весами 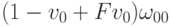 и
и 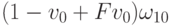 рациональной кривой Безье и берем на ней точку с параметром
рациональной кривой Безье и берем на ней точку с параметром ![u = u_0 \in [0,1] .](/sites/default/files/tex_cache/c0847213388f05ea63d0258535c7a2e3.png)
Полученная точка и будет точкой с параметрами  на рациональной поверхности Безье, построенной по
на рациональной поверхности Безье, построенной по 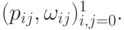
Деление поверхности Безье
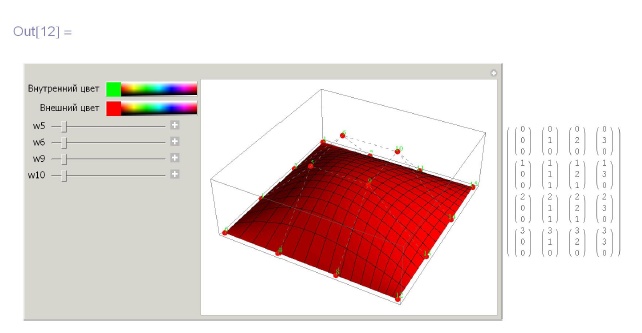
Деление поверхностей Безье целиком основано на делении кривых Безье. Как мы уже знаем, каждая из кривых Безье (обычных или рациональных), построенных по столбцам сетки опорных точек  может быть разделена в параметрической точке
может быть разделена в параметрической точке ![u = u^* \in [0,1]](/sites/default/files/tex_cache/2ce4211e714f21e71a174703be30e2c5.png) без изменения ее формы. При таком делении получаются две поверхности Безье (составляющие вкупе исходную поверхность) и соответствующие им две матрицы опорных точек Безье, каждая из которых имеет тот же порядок, что и исходная матрица:
без изменения ее формы. При таком делении получаются две поверхности Безье (составляющие вкупе исходную поверхность) и соответствующие им две матрицы опорных точек Безье, каждая из которых имеет тот же порядок, что и исходная матрица:  и
и  Затем, каждую из получившихся двух поверхностей Безье надо поделить в параметрической точке
Затем, каждую из получившихся двух поверхностей Безье надо поделить в параметрической точке 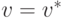 (с помощью деления кривых Безье, построенных по строкам соответствующих матриц). В итоге получится четыре поверхности Безье и соответствующие им четыре матрицы опорных точек:
(с помощью деления кривых Безье, построенных по строкам соответствующих матриц). В итоге получится четыре поверхности Безье и соответствующие им четыре матрицы опорных точек: 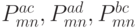 и
и 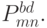 Эти четыре поверхности Безье будут лежать на исходной поверхности Безье, делить ее на четыр
е части и в совокупности составлять исходную поверхность.
Эти четыре поверхности Безье будут лежать на исходной поверхности Безье, делить ее на четыр
е части и в совокупности составлять исходную поверхность.
Новые сети опорных точек 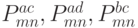 и
и  получаются из исходной сети
получаются из исходной сети  по следующим формулам, аналогичным формулам (5.26):
по следующим формулам, аналогичным формулам (5.26):