| Украина |
Графика: основные принципы
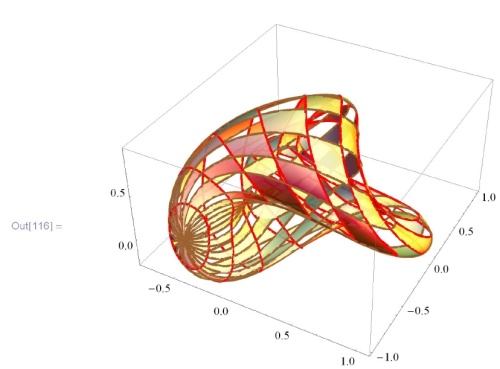
Координатные линии на поверхности, соответствующие параметризации, можно увидеть, сменив  . Заодно разрежем поверхность в шахматном порядке:
. Заодно разрежем поверхность в шахматном порядке:
![\tt
In[116]: =
\phantom{In}ParametricPlot3D[r[$\theta$, $\varphi$], \{$\theta$, -$\pi$/2, $\pi$/2\}, \{$\varphi$, 0, $\pi$\},\\
\phantom{InP}MeshFunctions $\to$ \{\#4 \&, \#5 \&\},\\
\phantom{InP}MeshShading $\to$
\phantom{InPa}\{\{Directive[\{Orange, Opacity[0.9], Specularity[White, 2]\}],\\
\phantom{InPara}None\},\\
\phantom{InPar}\{None, Directive[$\setminus$\{Orange, Opacity[0.9],\\
\phantom{InParame}Specularity[White, 2]\}]\}\}, PlotPoints $\to$ 30,\\
\phantom{InP}PlotStyle $\to$ \{Opacity[0.5]\},\\
\phantom{InP}MeshStyle $\to$ \{\{Thick, Red\}, \{Thick, Brown\}\}]](/sites/default/files/tex_cache/40642825cf83f79e7491fae3a7709ed9.png)
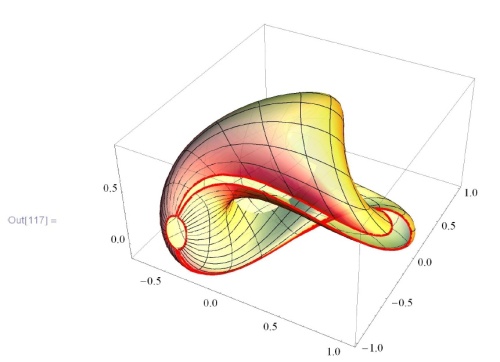
Наконец, чтобы лучше себе представить параметризацию, выбросим края параметризующего прямоугольника. Граница выделяется с помощью опции 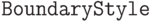 :
:
![\tt
In[117]:=\\
\phantom{In}ParametricPlot3D[r[$\theta$, $\varphi$], \{$\theta$, -$\pi$/2 + 0.1, $\pi$/2 - 0.1\}, \\
\phantom{InP}\{$\varphi$, 0.1, $\pi$ - 0.1\}, MeshFunctions $\to$ \{\#4 \&, \#5 \&\}, PlotPoints $\to$ 30,\\
\phantom{InP}PlotStyle $\to$ \{Orange, Opacity[0.9], Specularity[White, 2]\},\\
\phantom{InP}BoundaryStyle $\to$ \{Red, Thick\}]](/sites/default/files/tex_cache/1cb4889447946ee3968e5a953b9c697b.png)
Нарисуем теперь отдельно вырезанный фрагмент. Каждый кусочек нарисуем отдельно, не выводя на экран, не забыв сделать одинаковыми изображаемые области с помощью  :
:
![\tt
In[118]:=\\
\phantom{In}gr=\{ParametricPlot3D[r[$\theta$, $\varphi$], \{$\theta$, - $\pi$/2, - $\pi$/2 + 0.1\},\\
\phantom{Ingr=}\{$\varphi$, 0, $\pi$\}, BoundaryStyle $\to$ \{Red, Thick\}, Mesh $\to$ None,\\
\phantom{Ingr=}PlotRange $\to$ 1.2], ParametricPlot3D[r[$\theta$, $\varphi$],\\
\phantom{Ingr=}\{$\theta$, $\pi$/2 - 0.1, $\pi$/2\}, \{$\varphi$, 0, $\pi$\}, BoundaryStyle $\to$ \{Red, Thick\},\\
\phantom{Ingr=}Mesh $\to$ None, PlotRange $\to$ 1.2],\\
\phantom{Ingr}ParametricPlot3D[r[$\theta$, $\varphi$], \{$\theta$, - $\pi$/2, $\pi$/2\}, \{$\varphi$, 0, 0.1\},\\
\phantom{Ingr=}BoundaryStyle $\to$ \{Red, Thick\}, Mesh $\to$ None, PlotRange $\to$ 1.2],\\
\phantom{Ingr}ParametricPlot3D[r[$\theta$, $\varphi$], \{$\theta$, -$\pi$/2, $\pi$/2\}, \{$\varphi$, $\pi$ - 0.1, $\pi$\},\\
\phantom{Ingr=}BoundaryStyle $\to$ \{Red, Thick\}, Mesh $\to$ None, PlotRange $\to$ 1.2]\};](/sites/default/files/tex_cache/cb76937cba3fa3551b89223c40d68941.png)
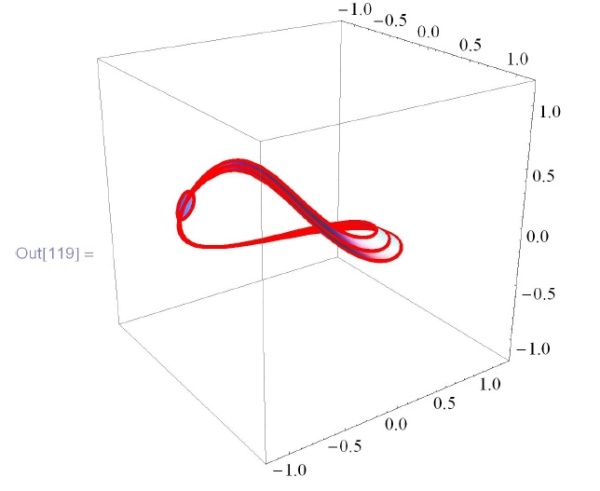
А теперь посмотрим все сразу с помощью  и, окончательно, увидим лист Мебиуса, заклеивающий границу диска:
и, окончательно, увидим лист Мебиуса, заклеивающий границу диска:
![\tt In[119]:=Show[gr]](/sites/default/files/tex_cache/d9a6319afca51dc7e2b55f0ac99d3585.png)
Покажем теперь, как можно раскрасить поверхность в соответствии с ее гауссовой кривизной. Сначала вычислим кривизну:
![In[120]:=\\
\phantom{In}ClearAll[r, к, u, v, norm, iiForm];\\
\phantom{In}iForm[r\_][u\_, v\_] := Module[\{ru, rv\},\\
\phantom{IniFo}ru = D[r[u, v], u]; rv = D[r[u, v], v];\\
\phantom{IniFo}$\begin{pmatrix}
ru.ru & ru.rv \\
ru.rv & rv.rv \\
\end{pmatrix}$\\
\phantom{IniF}];\\
\phantom{In}norm[r\_][u\_, v\_] := Module[\{ru, rv, nn\},\\
\phantom{Innor}ru = D[r[u, v], u]; rv = D [r[u, v], v]; nn = Cross[ru, rv];\\
\phantom{Innor}$\frac{nn}{\sqrt{nn.nn}}$\\
\phantom{Inno}];\\
\phantom{In}iiForm[r\_][u\_, v\_] := Module[\{ruu, ruv, rw, n\},\\
\phantom{IniiF}n = norm[r][u, v];\\
\phantom{IniiF}ruu = D [r[u, v], u, u]; ruv = D[r[u, v], u, v];\\
\phantom{IniiF}rvv = D [r[u, v], v, v];\\
\phantom{IniiF}$\begin{pmatrix}
ruu.n & ruv.n \\
ruv.n & rw.n
\end{pmatrix}$\\
\phantom{Inii}];\\
\phantom{In}k[r\_][u\_, v\_] := $\frac{\text{Det}[\text{iiForm}[r][u,v]]}{\text{Det}[\text{iForm}[r][u,v]]}$;](/sites/default/files/tex_cache/de18b3398691bfbf53ba11a073666f3b.png)
Параметризуем тор:
![\tt
In[125]:=\\
\phantom{In}ClearAll[R, r, $\varphi$, $\psi$, torus, g, kMax, kMin, kRescaled];\\
\phantom{In}res=$\begin{pmatrix}
\text{Cos}[\varphi]& \text{-Sin}[\varphi]& 0\\
\text{Sin}[\varphi]& \text{Cos}[\varphi]& 0\\
0&0&1
\end{pmatrix}$.(\{0, R, 0\} + \{0, rCos[$\psi$], rSin[$\psi$]\})\\
\phantom{Inres}Simplify;\\
\phantom{In}R = 3; r = 1; \\
\phantom{In}torus[$\varphi$\_, $\psi$\_] := \{-(R + rCos[$\psi$]) Sin[$\varphi$], Cos[$\varphi$](R + rCos[$\psi$]),\\
\phantom{Inres}RSin[$\psi$]\};
\end{pmatrix}](/sites/default/files/tex_cache/f8230d21114b55d8d8ca645f372a62e1.png)
Масштабируем кривизну так, чтобы она принимала значения от 1 до 1/2:
![\tt
In[129]:=g[u\_, v\_]=k[torus][u, v] // Simplify;\\
\phantom{In[129]:=}kMax = Maximize[g[u, v], \{u, v\}][\!\![1]\!\!];\\
\phantom{In[129]:=}kMin = Minimize[g[u, v], \{u, v\}][\!\![1]\!\!];\\ \\
In[132]:=kRescaled[u\_, v\_] := $\frac{g[u,v]\text{-kMin}}{1.2(\text{kMax-kMin})}$;](/sites/default/files/tex_cache/12697d98fe6b095eceab6440c54e1243.png)
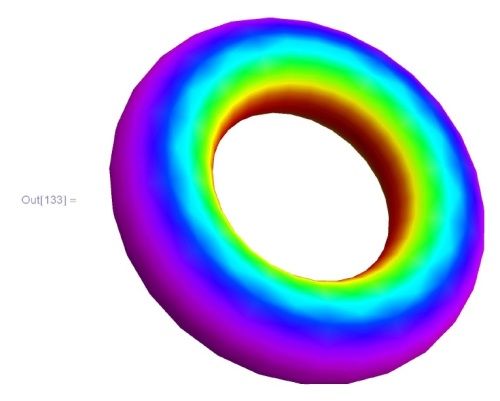
Теперь раскрашиваем тор с помощью ColorFunction:
![\tt
In[133]:=ParametricPlot3D[torus[$\varphi$, $\psi$], \{$\varphi$, 0, 2$\pi$\}, \{$\psi$, 0, 2$\pi$\},\\
\phantom{In[133]:=P}Boxed $\to$ False, Axes $\to$ False,\\
\phantom{In[133]:=P}ColorFunction $\to$ Function[\{x, y, z, u, v\},\\
\phantom{In[133]:=PCo}Hue[kRescaledfu, v]]], ColorFunctionScaling $\to$ False,\\
\phantom{In[133]:=P}Mesh $\to$ None]](/sites/default/files/tex_cache/16e9bf76a5788484c34aba537af4e160.png)
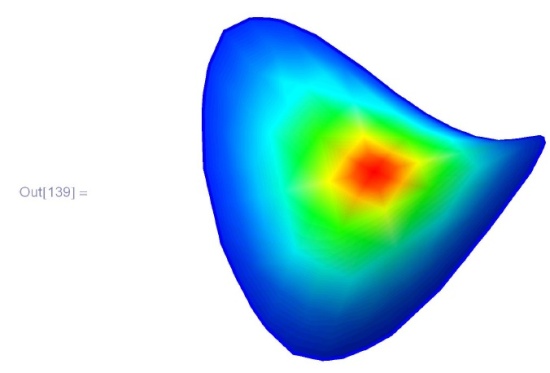
или седловую поверхность:
![\tt
In[134]:=\\
\phantom{In}sadd[x\_, y\_] := \{x, y, x$^2^ - y$^2$};\\
\phantom{In}kM[x\_, y\_] := k[sadd][x, y] // Simplify;\\
\phantom{In}kMax = Maximize[kM[u, v], u$^2$ + v$^2$ $\le$ 2, \{u, v\}][\!\![1]\!\!];\\
\phantom{In}kMin = Minimize[kM[u, v], \{u, v\}][\!\![1]\!\!];\\
\phantom{In}kRes[u\_, v\_]=$\frac{\text{kM}[u,v]-\text{kMin}}{1.4 (\text{kMax-kMin})}$;\\
\phantom{InP}ParametricPlot3D[sadd[x, y], \{x, -2, 2\}, \{y, -2, 2\},\\
\phantom{InP}Boxed $\to$ False, Axes $\to$ False,\\
\phantom{InP}RegionFunction $\to$ Function[\{x, у, z, u, v\}, (x$^2$ + y$^2$ < 1/2)],\\
\phantom{InP}ColorFunction $\to$ Function[\{x, y, z, u, v\}, Hue[kRes[х, y]]],\\
\phantom{InP}ColorFunctionScaling $\to$ False, Mesh $\to$ False,\\
\phantom{InP}BoundaryStyle $\to$ \{Thick, Blue\}]](/sites/default/files/tex_cache/569171a95b7c2dbf2ad4b3f0b305f6d6.png)
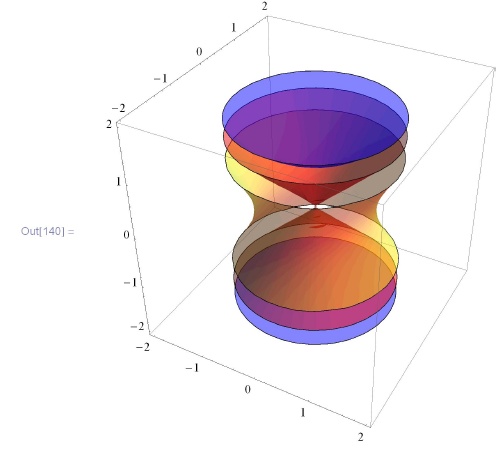
Поверхности уровня удобно рисовать с помощью  , в аргументах которой указывается функция, интервалы значения переменных, какие (или сколько именно) значения функции рисовать (
, в аргументах которой указывается функция, интервалы значения переменных, какие (или сколько именно) значения функции рисовать (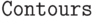 приписывается количество значений или их список), директивы, описывающие, как именно рисовать поверхности (
приписывается количество значений или их список), директивы, описывающие, как именно рисовать поверхности ( приписывается список директив)):
приписывается список директив)):
![\tt
In[140]:=\\
\phantom{In}ContourPlot3D[x$^2$ + у$^2$ - z$^2$, \{x, -2, 2\}, \{у, -2, 2\}, \{z, -2, 2\},\\
\phantom{InC}Contours $\to$ \{-1, 0, 1\},\\
\phantom{InC}ContourStyle $\to$ Мар[\{\#, Opacity[0.5]\} \&, \{Blue, Red, Yellow\}],\\
\phantom{InC}Mesh $\to$ None, RegionFunction $\to$ (\#1$^2$ + \#2$^2$ < 2 \&)]](/sites/default/files/tex_cache/141f1da18878112b90265dec3ce5a949.png)
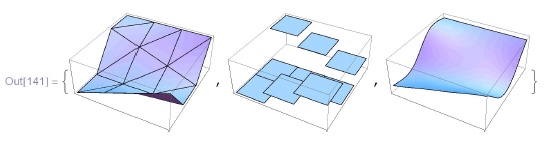
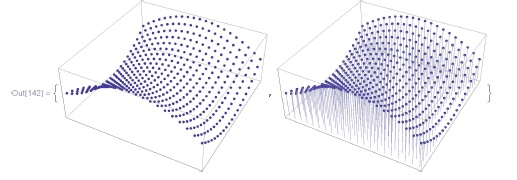
Следующие команды  служат для визуализации дискретных наборов чисел:
служат для визуализации дискретных наборов чисел:
![\tt
In[141]:=\{ListPlot3D[\{\{l, 2, 3, 4\}, \{1, 1, 1, 1\}, \{4, 3, 2, 1\},\\
\phantom{In[141]:=\{Li}\{4, 4, 4, 4\}\}, Mesh $\to$ All],\\
\phantom{In[141]:=\{}ListPlot3D[\{\{l, 2, 3, 4\}, \{1, 1, 1, 1\}, \{4, 3, 2, 1\},\\
\phantom{In[141]:=\{Li}\{4, 4, 4, 4\}\}, Mesh $\to$ None, InterpolationOrder $\to$ 0],\\
\phantom{In[141]:=\{}ListPlot3D[\{\{l, 2, 3, 4\}, \{1, 1, 1, 1\}, \{4, 3, 2, 1\},\\
\phantom{In[141]:=\{Li}\{4, 4, 4, 4\}\}, Mesh $\to$ None, InterpolationOrder $\to$ 3]\}](/sites/default/files/tex_cache/89f13e2c899c0da0fa94dd3716ca4df3.png)
![\tt
In[142]:=\\
\phantom{In}\{ListPointPlot3D[Table[i$^2$ - j$^2$, \{i, -1, 1, 0.1\},\\
\phantom{In\{Li}\{j, -1, 1, 0.1\}]],\\
\phantom{In\{}ListPointPlot3D[Table[i$^2$ - j$^2$, \{i, -1, 1, 0.1\}, \{j, -1, 1, 0.1\}],\\
\phantom{In\{L}Filling $\to$ Bottom]\}](/sites/default/files/tex_cache/efca086bb15d4ac873206b56ee73d580.png)
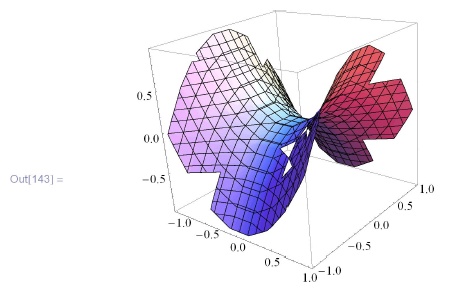
Наконец,  служит для визуализации набора точек в пространстве:
служит для визуализации набора точек в пространстве:
![\tt
In[143]:=\\
\phantom{In}ListSurfacePlot3D[\\
\phantom{InL}Flatten[Table[\{i, j, i$^2$ - j$^2$\}, \{i, -1, 1, 0.1\}, \{j, -1, 1, 0.1\}],\\
\phantom{InLi}1]]](/sites/default/files/tex_cache/056c460cb0c4980836c89a509c74ee9a.png)
а команда  - для изображения множеств, заданных неравенствами:
- для изображения множеств, заданных неравенствами:
![\tt
In[144]:=RegionPlot3D[-1$\le$х$\le$1 \&\& -1$\le$у$\le$1 \&\& -0.2$\le$z$\le$0.2 \&\&\\
\phantom{In[144]:=Re}Not[-1/2$\le$х$\le$1/2 \&\& -1/2$\le$у$\le$1/2], \{х, -2, 2\},\\
\phantom{In[144]:=R}\{у, -2, 2\}, \{z, -2, 2\}, Mesh $\to$ None, PlotPoints $\to$ 50,\\
\phantom{In[144]:=R}Axes $\to$ None, Boxed $\to$ False, PlotStyle $\to$ \{Pink\}]](/sites/default/files/tex_cache/aa1681c71f1ff3651c925fbed6e7d07d.png)