| Украина |
Инспектор
Вы можете этот курс.
Опубликован: 27.12.2010 | Уровень: специалист | Доступ: платный
Лекция 2:
Графика: основные принципы
Трехмерная графика
Практически все команды двумерной графики имеют аналоги в трехмерной. Снова рассмотрим сначала простейшую команду рисования графика функции двух переменных 
:
![\tt
In[103]:=Plot3D[уSin[x] + уSin[x], \{x, -$\pi$, $\pi$\}, \{у, -$\pi$, $\pi$\}]](/sites/default/files/tex_cache/814b442e9e70a3da760d71896b53024b.png)
Эта команда порождает графический комплекс с заданными нормалями вершин:
![\tt
In[104]:=\\
\phantom{In}InputForm[Plot3D[уSin[х] + уSin[х], \{х, -$\pi$, $\pi$\}, \{у, -$\pi$, $\pi$\}]] // \\
\phantom{InI}Short \\ \\
Out[104]=Graphics3D[GraphicsComplex[\{\{<<3>>\},\\
\phantom{Out[104]=Gr}\{<<3>>\}, <<2526>>, \{<<3>>\}\}, <<2>>], \{<<5>>\}]](/sites/default/files/tex_cache/624cdcd94ff74b469d545d4a807b5d14.png)
точнее,
![\tt
In[105]:=\\
\phantom{In}Plot3D[уSin[x] + ySin[x], \{x, -$\pi$, $\pi$\}, \{у, -$\pi$, $\pi$\},\\
\phantom{InP}PlotStyle$\to$FaceForm[Red, Blue], PlotPoints$\to$2 , Mesh$\to$All,\\
\phantom{InP}MaxRecursion$\to$0]](/sites/default/files/tex_cache/b5fa4be8b322c6039589270ab861a30a.png)
![\tt
In[106]:=\\
\phantom{In}InputForm[Plot3D[уSin[x] + уSin[х], \{х, -$\pi$, $\pi$\}, \{у, -$\pi$, $\pi$\},\\
\phantom{InIn}PlotPoints $\to$ 2, Mesh $\to$ All, PlotStyle $\to$ MaxRecursion $\to$ 0]]\\ \\
Out[106]=\\ \\
\phantom{O}Cruahics3D[\\
\phantom{Ou}GraphicsComplex[\{\{-3.141586370404486, -3.141586370404486, 0.00003947833864787322\},\\
\phantom{OuGr}\{3.141586370404486, -3.141586370404486, -0.00003947833864787322\},\\
\phantom{OuGr}\{-3.141586370404486, 3.141586370404486, -0.00003947833864787322\},\\
\phantom{OuGr}\{3.141586370404486, 3.141586370404486, 0.00003947833864787322\},\\
\phantom{OuGr}\{0., 0., 0.\},\{3.141586370404486, 0., 0.\}, \{0., 3.141586370404486. 0.\},\\
\phantom{OuGr}\{-3.141586370404486, 0., 0.\}, \{0., -3.141586370404486, -0.\},\\
\phantom{OuGr}\{-1.570793185202243, -1.570793185202243, 3.141586370388983\},\\
\phantom{OuGr}\{1.570793185202243, -1.570793185202243, 3.141586370388983\},\\
\phantom{OuGr}\{1.570793185202243, 1.570793185202243, 3.141586370388983\},\\](/sites/default/files/tex_cache/4dd7e490da15a1f9ec85e01ba9de968a.png)
![\tt
\phantom{OuG}\{\{\{EdgeForm[GrayLevel[0.]], MaxRecursion -> 0,\\
\phantom{OuGrap}GraphicsGroup[\{Polygon[\{\{11,6,5\}, \{14,12,6\}, \{13,8,5\}, \{10,9,5\},\\
\phantom{OuGrapGrap}\{12,7,5\}, \{15,13,7\}, \{8,10,5\}, \{16,10,8\}, \{17,11,9\},\\
\phantom{OuGrapGrap}\{18,10,1\}, \{20,12,4\}, \{13,15,3\}, \{11,17,2\}, \{10,18,9\},\\
\phantom{OuGrapGrap}\{12,14,2\}, \{20,12,4\}, \{13,15,3\}, \{11,17,2\}, \{10,18,9\}\\
\phantom{OuGrapGrap}\{11,19,6\}, \{10,16,1\}, \{12,20,7\}, \{13,21,8\}\}]\}]\}, \{\},\{\},\{\},\{\}\}\},\\](/sites/default/files/tex_cache/96f4462993e54cec56805020320a75a4.png)
![\tt
\phantom{OuGra}\{0.952890338648335, -3.811568977840421*\^\,\!-6, 0.30331502187681625\},\\
\phantom{OuGra}\{-8.827624885274624*\^\,\!-6, 0.894427190964183, 0.4472135954829845\},\\
\phantom{OuGra}\{-0.952890338648335, 3.811568977840421*\^\,\!-6, 0.30331502187681625\},\\
\phantom{OuGra}\{8.827624885274624*\^\,\!-6, -0.894427190964183, 0.44721359548429548\},\\
\phantom{OuGra}\{8.827624885274624*\^\,\!-6, 0.894427190964183, 0.44721359548429548\},\\
\phantom{OuGra}\{-0.952890338648335, -3.811568977840421*\^\,\!-6, 0.30331502187681625\},\\
\phantom{OuGra}\{-8.827624885274624*\^\,\!-6, -0.894427190964183, 0.44721359548429548\},\\
\phantom{OuGra}\{0.952890338648335, 3.811568977840421*\^\,\!-6, 0.30331502187681625\},\\
\phantom{Ou}{Axes -> True, BoxRatios -> {1, 1, 0.4}, Method -> {"RotationControl"\ \!\!\!\! -> "Globe"\ \!\!\!\!\},\\
\phantom{OuG}PlotRange -> \{\{Pi, Pi\}, \{-Pi, Pi\}, \{-6.283172740777966, 6.283172740777966\}\},\\
\phantom{OuG}PlotRangePadding -> \{Scaled[0.02], Scaled[0.02], Scaled[0.02]\}\}]](/sites/default/files/tex_cache/faccc02be724ad69d9140273a4f8e5e5.png)
Снова можно пользоваться стандартными опциями трехмерной графики, снова есть 
для директив. Из новых опций обратим внимание на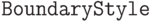 
(приписывается графическая директива, описывающая граничную линию), 
и 
(исключение части рисунка, заданной условием, и способ прорисовки ограничивающей линии), 
(задание области рисунка с помощью функции от стандартного набора переменных), 
(приписывается функция или функции, линии уровня которых задают координатные линии на поверхности), 
(приписывается количество этих линий):
![\tt
In[107]:=\\
\phantom{In}Plot3D[уSin[х] + уSin[х], \{х, -$\pi$, $\pi$\}, \{у, -$\pi$, $\pi$\},\\
\phantom{InP}MeshFunctions $\to$ \{\#3 \&\}, MeshStyle $\to$ \{Orange\},\\
\phantom{InP}PlotStyle $\to$ FaceForm[Directive[Red, Specularity[White, 2]],\\
\phantom{InPlo}Blue], BoundaryStyle $\to$ \{Thick, Red\}]](/sites/default/files/tex_cache/0685685d76e5804ae6880b6953a5b011.png)
![\tt
In[108]:=\\
\phantom{In}Plot3D[ySin[x] + ySin[x], \{x, -$\pi$, $\pi$ \}, \{у, -$\pi$, $\pi$\},\\
\phantom{InP}PlotStyle $\to$ FaceForm[Directive[Red, Specularity[White, 2]],\\
\phantom{InPPl}Blue], BoundaryStyle $\to$ \{Thick, Red\},\\
\phantom{InP}MeshFunctions $\to$ \{(\#1$^2$ + \#2$^2$) \&\}, Mesh $\to$ 5,\\
\phantom{InP}RegionFunction $\to$ Function[\{x, у, z\}, 1/2 < x$^2$ + у$^2$ > 3]]](/sites/default/files/tex_cache/af29abce46fb56de2685f385719aae22.png)
Из других команд отметим прежде всего команды, позволяющие рисовать параметрически заданные поверхности и кривые (
и ее частные случаи 
и 
), неявно заданные поверхности (
), трехмерные области, заданные неравенствами (
), а также трехмерные рисовалки дискретных данных, такие как 
.
В качестве примера рассмотрим знаменитую поверхность Боя - параметризацию проективной плоскости. Явные формулы взяты из задачника А. С. Мищенко, Ю. П. Соловьева, А. Т. Фоменко [5].
![\tt
In[109]:=\\
\phantom{In}ClearAll[x, y, z, $\theta$, $\varphi$, f1, f2, f3, r];\\
\phantom{In}f1=[$\theta$\_, $\varphi$\_] :=\\
\phantom{Inf1}$\frac12$((2x$^2$ - y$^2$ - z$^2$)(x$^2$ + y$^2$ + z$^2$) + 2yz(y$^2$-z$^2$) + zx(x$^2$ - z$^2$) +\\
\phantom{In$\frac12$((}xy(y$^2$ - x$^2$)) /. \{x $\to$ Cos[$\theta$] Cos[$\varphi$], y $\to$ Cos[$\theta$]Sin[$\varphi$],\\
\phantom{In$\frac12$}z $\to$ Sin[$\theta$]\};\\
\phantom{In}f2[$\theta$\_, $\varphi$\_] :=\\
\phantom{Inf2}$\frac{\sqrt{3}}{2}$((y$^2$ - z$^2$) (x$^2$ + y$^2$ + z$^2$) + zx(z$^2$ - x$^2$) + xy(y$^2$ - x$^2$)) /.\\
\phantom{Inf2[}\{x $\to$ Cos[$\theta$] Cos[$\varphi$], y $\to$ Cos[$\theta$] Sin[$\varphi$], z $\to$ Sin[$\theta$]\};\\
\phantom{In}f3[$\theta$\_, $\varphi$\_] := (x + y + z) ((x + y + z)$^3$ + 4(y-x) (z-y) (x-z)) /.\\
\phantom{Inf3[}\{x $\to$ Cos[$\theta$ Cos[$\varphi$], y $\to$ Cos[$\theta$]Sin[$\varphi$], z $\to$ Sin[$\theta$]\};\\
\phantom{In}r[$\theta$\_, $\varphi$\_] := \{f1[$\theta$, $\varphi$], f2[$\theta$, $\varphi$], 0.1f3[$\theta$, $\varphi$]\};](/sites/default/files/tex_cache/e5bbc227cc1c42e3dd15189327c54944.png)
Сначала нарисуем эту сложную самопересекающуюся поверхность, разрезая ее на горизонтальные слои и выбрасывая каждый второй, чтобы можно было лучше рассмотреть самопересечения. Это делается с помощью опций 
(устанавливается в функцию от стандартных переменных), 
(определяет, что рисовать между - линиями, присваивается список (списки) циклически повторяющихся директив; 
соответствует "ничего не рисованию") и или количество равномерно распределенных линий, или явные значения .
![\tt
In[114]:=\\
\phantom{In}ParametricPlot3D[r[$\theta$, $\varphi$], \{$\theta$, -$\pi$/2, $\pi$/2\}, \{$\varphi$, 0, $\pi$\},\\
\phantom{InP}MeshFunctions $\to$ \{\#3 \&\},\\
\phantom{InP}MeshShading $\to$
\phantom{InPa}\{Directive[\{Orange, Opacity[0.9], Specularity[White, 2]\}],\\
\phantom{InPar}None\}, PlotPoints $\to$ 30,\\
\phantom{InP}Mesh $\to$ \{\{-0.05, 0.05, 0.1, 0.2, 0.3, 0.4\}\}]](/sites/default/files/tex_cache/be41551691032bc0ff47a6a32f39aa96.png)
Выделить наиболее сложный фрагмент поверхности можно с помощью опции :
![\tt
In[115]:=\\
\phantom{In}ParametricPlot3D[r[$\theta$, $\varphi$], \{$\theta$, -$\pi$/2, $\pi$/2\}, \{$\varphi$, 0, $\pi$ \},\\
\phantom{InP}PlotStyle $\to$ Directive[\{Orange, Opacity[0.9]\}], Mesh $\to$ None, \\
\phantom{InP}PlotPoints $\to$ 30,\\
\phantom{InP}RegionFunction $\to$ Function[\{x, у, z\}, 0.05 < z < 0.2], \\
\phantom{InP}Boxed $\to$ False, Axes $\to$ None]](/sites/default/files/tex_cache/74cffbaefe56d617dda570541c8fa7b4.png)
