| Казахстан, Алматы |
Вычисления с оракулом
Теорема Мучника-Фридберга: выигрышные условия
Итак, пусть фиксирована программа p, которой Р хочет помешать разрешать множество X относительно множества Y. Что он должен для этого делать? (Мы будем описывать все происходящее с его точки зрения.)
В начале Р получает некоторое указание и некоторый элемент, с ним согласованный. Все дальнейшие указания должны быть сильнее этого мы всегда должны указывать включить определенные числа в X и Y и не включать некоторые другие (и тех, и других конечное множество). Кроме того, есть некоторый начальный элемент начальная пара множеств. Со временем И увеличивает эти множества по собственному усмотрению; единственное, как мы можем на это повлиять давая указания.
Итак, что же мы делаем? На первом шаге выберем какое-то число x, не входящее в начальное значение X и не затронутое начальным указанием. В нашем первом указании мы попросим не включать это x в X, то есть добавим x во вторую компоненту начального указания, которую мы когда-то обозначали A-. (Если бы мы хотели, чтобы программа не разрешала Y, мы бы действовали симметрично и добавляли бы число в четвертую компоненту, которая обозначалась B-.)
Что это нам дает? Если мы будем и дальше дублировать первое указание, то мы добьемся, чтобы число x не принадлежало предельному множеству X. Но если в какой-то момент мы передумаем и захотим, чтобы x принадлежало X, это можно достаточно изъять x из A- и добавить его в A+, что не вызовет пата. (Заметим, что это новое указание не будет сильнее прежнего но по-прежнему будет сильнее начального, а только это и требуется.)
Так или иначе, мы выбрали такое x, сформировали первое указание и дублируем его, пока не видим причин изменить свое мнение. Причины эти могут состоять в следующем. На n -ом ходу игры мы выполняем n шагов работы программы p на входе x. (Напомним, что p та самая программа, которой мы хотим не дать разрешать X с оракулом для Y.) При этом, когда программа вызывает внешнюю процедуру для Y, мы даем ответы в соответствии с текущим состоянием Y (то есть в соответствии с последним элементом, написанным И). Представим себе, что действительно за n шагов получился какой-то результат. Тогда мы пробуждаемся и смотрим, принадлежность и непринадлежность каких элементов множеству Y была при этом использована, и фиксируем текущее положение дел в нашем следующем и всех последующих (больше они меняться не будут) указаниях. Тем самым будет гарантирован тот же ответ программы p на предельном множестве Y. С другой стороны, мы можем добиться, чтобы x принадлежало X или нет по желанию (чтобы не принадлежало, не надо делать ничего, чтобы принадлежало перенесем его в положительную часть указания, см. выше). Сделаем это так, чтобы ответ программы p стал неправильным.
Покажем, что эта стратегия действительно выигрышная. Есть два случая. Если мы в какой-то момент пробудились, то по построению программа p дает неправильный ответ на числе x. Если же мы так и не пробудились, то программа p не дает на x никакого ответа (при предельном значении оракула). Почему? В самом деле, любой такой ответ зависит от конечного числа вопросов к оракулу и требует конечного числа шагов работы так что на достаточно далеком шаге игры, когда все нужные числа в оракуле появятся и времени на вычисление будет достаточно, мы должны были бы пробудиться.
Вычислимость нашей стратегии (в том числе вычислимая зависимость от параметра, то есть от программы p ) очевидна. Осталось объяснить лишь, почему число различных указаний будет конечно. На самом деле их может быть максимум два если мы когда-то пробуждались, чтобы далее заснуть навеки (а если не пробуждались, то вообще одно).
Теорема Мучника-Фридберга: метод приоритета
Теперь можно забыть о конкретной природе элементов и указаний и
показать, что если есть последовательность выигрышных условий 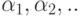 ., причем выигрышные стратегии для Р
вычислимо зависят от i, то есть пара перечислимых множеств,
удовлетворяющая всем условиям.
., причем выигрышные стратегии для Р
вычислимо зависят от i, то есть пара перечислимых множеств,
удовлетворяющая всем условиям.
Для этого представим себя на месте исполнителя, над которым есть последовательность руководителей, приоритеты которых убывают (первый самый важный, второй менее важный и т.д.). Каждый из руководителей отвечает за свое условие и имеет свою выигрышную стратегию. Вначале мы начинаем играть с первым руководителем и выполнять его указания. Когда они начинают повторяться, мы надеемся, что первый руководитель уже больше менять их не будет, и передаем текущий элемент и текущее указание в качестве начальных второму руководителю, и играем с ним. (Все указания второго будут сильнее временно стабилизировавшихся указаний первого.) Когда указания второго тоже стабилизируются, можно подключить третьего и т.д.
Что же происходит, если какой-то из руководителей неожиданно изменил свое указание? В этом случае мы следуем его указанию, не обращая внимания на указания менее приоритетных, а перед ними извиняемся и говорим, что пригласили их слишком рано. Но затем мы снова постепенно приглашаем их по той же схеме.
Покажем, что каждый руководитель рано или поздно получит возможность бессменно руководить. В самом деле, первый вообще ничего не знает о других, поскольку его указания самые важные и всегда исполняются. Значит, в некоторый момент он перестанет давать новые указания. Запущенная после этого инкарнация второго руководителя уже не встретит никаких помех, поскольку лишь изменение указаний первого может ей помешать, поэтому и указания второго стабилизируются, и т.д. При этом каждый руководитель добьется выполнения своего свойства.
Теперь видно, почему в определении игры были важны начальные элементы и условия настоящий Руководитель должен добиваться своего, исходя из любой начальной ситуации (кто знает, до чего доведут дело предыдущие!).
Вычислимость всех стратегий всех руководителей (плюс вычислимая зависимость от номера руководителя) гарантирует вычислимость описанного процесса, так что получатся перечислимые множества, которые удовлетворяют всем условиям.
Это рассуждение завершает доказательство теоремы Мучника-Фридберга.
62. Покажите, что существует счетное число перечислимых множеств, никакие два из которых не сравнимы по Тьюрингу.
