Вычисления с оракулом

Опишем рассуждение более подробно. Назовем фрагментом функцию, которая определена на некотором (конечном) начальном отрезке натурального ряда и принимает значения 0 и 1. Будем говорить, что множество A согласовано с фрагментом a, если характеристическая функция множества A продолжает a. Другими словами, согласованность с данным фрагментом означает определенное поведение множества на начальном отрезке натурального ряда.

Если фрагмент a₂ продолжает фрагмент a₁ (то есть определен на большем отрезке с сохранением прежних значений на меньшем), то, очевидно, согласованность с ним накладывает больше ограничений на множество.

Лемма. Пусть a и b два фрагмента, а p программа, содержащая вызовы внешней процедуры. Тогда существуют продолжения a' и b' этих фрагментов с таким свойством: ни для каких множеств A и B, согласованных с a' и b', программа p, имея доступ к характеристической функции для B, не будет разрешать множество A.

Доказав эту лемму, можно поочередно рассматривать все программы и гарантировать, что ни одна из них не разрешает A относительно B. Если при этом чередовать A и B в применении этой леммы, то одновременно можно гарантировать, что ни одна программа не разрешает B относительно A.

(Замечание. Очевидно, можно предполагать, что a' и b' длиннее a и b их всегда можно искусственно удлинить. Тогда в пределе мы получим бесконечные последовательности, являющиеся характеристическими функциями двух искомых множеств. Впрочем, это не обязательно: если в пределе вдруг получатся конечные фрагменты возьмем любые множества, с ними согласованные.)

Итак, для построения множеств A и B осталось доказать лемму. (К вопросу о 0' -вычислимости мы еще вернемся.)

В формулировку леммы множества A и B входят несимметрично, поэтому и рассуждение будет несимметричное. Фиксируем некоторое число x, которое не входит в область определения фрагмента a, и зададим себе вопрос: существует ли такое множество B, согласованное с фрагментом b, что после присоединения его характеристической функции к программе p эта программа дает на входе x какой-то из ответов " да" и " нет". Если такого множества нет, то вообще заботиться не о чем утверждение леммы будет верным, если просто положить a'=a, b'=b.

Пусть такое множество B существует. Проследим за работой программы p на входе x для этого множества B. Прежде чем выдать свой ответ, программа может некоторое конечное число раз вызывать характеристическую функцию множества B. Возьмем фрагмент b', с которым B согласовано, и притом достаточно длинный, чтобы покрыть и зафиксировать все те места, к которым обращалась программа p. Тогда программа p будет давать тот же самый ответ не только для множества B, но и для любых множеств, согласованных с b'. Остается обеспечить, чтобы этот ответ был неверным, что можно сделать, включив x в область определения a' и выбрав a'(x) противоречащим этому ответу. Лемма доказана.

Осталось лишь доказать утверждение теоремы, относящееся к 0' -вычислимости, для чего надо убедиться, что построение a' и b' в доказательстве леммы можно сделать 0' -алгоритмическим. Ключевой момент здесь ответ на сформулированный при доказательстве леммы вопрос. Конечно, буквально перебрать континуум возможных множеств B, согласованных с фрагментом b, невозможно. Но это и не требуется надо просто просматривать все варианты работы программы p. Когда она задает вопрос про не входящее в b число, просмотр разветвляется на два направления в зависимости от двух возможностей. Получается ветвящееся дерево вариантов, и вопрос состоит в том, получается ли ответ " да" или " нет" хоть на какой-то ветви. А этот вопрос можно переформулировать как вопрос о том, остановится ли некоторая программа (а именно, программа, просматривающая параллельно все ветви и останавливающаяся, как только на одной из них появится ответ " да" или " нет").

Это замечание и завершает доказательство теоремы.

Гораздо более сложен вопрос о том, существуют ли не просто 0' -разрешимые несравнимые по Тьюрингу множества, а перечислимые несравнимые по Тьюрингу множества. Эту проблему (так называемую проблему Поста независимо решили американский математик Фридберг и Альберт Абрамович Мучник; интересно, что для построения перечислимых несравнимых множеств они использовали один и тот же подход, который получил название " метод приоритета".

Теорема Мучника-Фридберга: схема конструкции

Теорема 50. Существуют несравнимые по Тьюрингу перечислимые множества.

Мы приводим доказательство этой теоремы как пример более изощренной техники, используемой в теории вычислимых функций. Однако надо иметь в виду, что в 1960-ые и 1970-ые годы передний край этой области ушел далеко за горизонт, и приводимое ниже рассуждение стало скорее образцом простоты, чем сложности.

Итак, мы хотим построить два перечислимых множества, ни одно из которых не сводится к другому по Тьюрингу. Мы будем строить их по шагам; на каждом шаге будет известна лишь конечная часть будущих множеств. Нам будет удобна такая терминология.

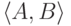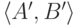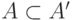Будем называть элементом произвольную пару конечных множеств натуральных чисел. Будем говорить, что элемент продолжает элемент , если и 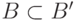. Мы построим вычислимую последовательность элементов, каждый из которых продолжает предыдущий; в пределе (объединении) они дадут искомые перечислимые несравнимые множества.

Будем называть указанием четверку конечных множеств 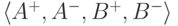, в которой A⁺ не пересекается с A^- и B⁺ не пересекается с B^-. Слово " указание" объясняется тем, что такие четверки указывают, чего мы хотим от элементов: A⁺ это числа, которые должны входить в A, а A^- числа, которые не должны входить в A ; аналогично для B. Формально, мы говорим, что элемент согласован с указанием , если 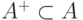, , 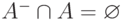, 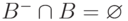. Будем говорить, что указание u_2 сильнее указания u₁, если всякий элемент, согласованный с u₂, согласован и с u₁ (то есть каждая из четырех частей указания может только увеличиться).

Пусть 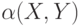произвольное свойство пары множеств 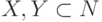. С каждым таким свойством свяжем некоторую игру двух персонажей Руководителя (Р) и Исполнителя (И). Игра происходит так: вначале И предъявляет Р некоторое указание u₀ и некоторый элемент e₀, согласованный с u₀. Мы будем называть их начальным указанием и начальным элементом. (Как мы увидим, в окончательной конструкции руководителей будет несколько, и начальное указание и элемент достаются свеженазначенному руководителю от его предшественников но об этом дальше). Р отвечает некоторым указанием u₁, после этого И выбирает согласованный с ним элемент e₁, затем Р выбирает u₂, И выбирает e₂ и так далее (игра продолжается бесконечно). При этом:

• Каждый следующий выбираемый И элемент должен продолжать предыдущий (и потому все они продолжают начальный); он также должен быть согласован с последним указанием Р, но может не быть согласован с его предыдущими указаниями.
• Все указания Р должны быть сильнее начального указания (но не обязаны быть сильнее его предыдущих указаний!).
• Если очередное указание Р вызывает пат (то есть у И нет элемента, который был с ним согласован и продолжал предыдущий элемент), то игра заканчивается и Р проигрывает.
• Если игра бесконечна, то мы считаем Р победителем при выполнении двух условий. Первое из них состоит в том, что указания Р, начиная с некоторого момента игры, не меняются.
• Наконец, второе условие состоит в том, что предельные множества X и Y удовлетворяют условию 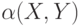, о котором мы говорили до начала описания игры. (Если i -ый элемент e_i есть 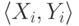, то X и Y есть объединения возрастающих цепочек множеств . и .)

Будем называть условие выигрышным, если существует вычислимая (реализуемая алгоритмом) стратегия для Р, гарантирующая его выигрыш. Дальнейший план действий такой. Мы покажем, что для любой программы p с вызовами внешней процедуры условие " p с оракулом для Y не разрешает X " является выигрышным. (Это рассуждение в значительной мере повторяет рассуждение из теоремы Клини-Поста, но несколько более сложно.) Более того, мы установим, что соответствующая стратегия вычислимо зависит от p.

С другой стороны, мы покажем, что для любого числа выигрышных условий 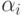, для которых стратегии можно выбрать вычислимо зависящими от i, можно найти пару перечислимых множеств, удовлетворяющую всем условиям. Именно это последнее рассуждение будет использовать идею " приоритета": у нас будет один исполнитель и счетное число руководителей, которым присвоены разные уровни приоритета (главный, менее главный, еще менее главный и т.д.).