| Казахстан, Алматы |
m-сводимость и свойства перечислимых множеств
m-сводимость
Мы уже встречались с таким приемом: чтобы доказать неразрешимость некоторого множества X (например, множества всех номеров всех где-то определенных функции), мы показывали, что если бы оно было разрешимо, то и любое перечислимое множество K было разрешимо. Для этого мы строили вычислимую функцию f так, чтобы принадлежность любого числа n множеству K определялась принадлежностью числа f(n) множеству X.
Сейчас мы изучим такие ситуации более подробно.
Говорят, что множество A натуральных чисел m - сводится к другому множеству B натуральных чисел, если существует всюду определенная вычислимая функция f : N -> N с таким свойством:
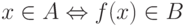
для всех  .
Такая функция называется m -сводящей A к B. Обозначение: A <=m B.
.
Такая функция называется m -сводящей A к B. Обозначение: A <=m B.
Теорема 31.(а) Если A <=m B и B разрешимо, то A разрешимо.(б) Если A <=m B и B перечислимо, то A перечислимо. (в) A <=m A ; если A <=m B и B <=m C, то A <=m C. (г) Если A <=m B, то N \ A <=m N \ B.
Все эти свойства почти очевидны. Пусть A <=m B и мы имеем разрешающий алгоритм для B. Чтобы узнать, принадлежит ли данное x множеству A, мы вычисляем f(x) и узнаем, принадлежит ли f(x) множеству B. Другими словами, a(x)=b(f(x)), если a характеристическая функция множества A, а b характеристическая функция множества B ; поэтому если b вычислима, то и a вычислима как композиция вычислимых функций.
Такое же равенство можно записать для " полухарактеристических " функций, поэтому из перечислимости B следует перечислимость A. Можно сказать и иначе: множество A является прообразом перечислимого множества B при вычислимом отображении f, и потому перечислимо.
Тождественная функция, очевидно, m -сводит A к A. Если функция f сводит A к B, а функция g сводит B к C, то
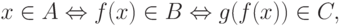
так что композиция функций g и f сводит A к C.
Наконец, функция, сводящая A к B, будет сводить и N \ A к N \ B.
Буква " m " в названии исторически происходит из термина "many-one-reducibility"; впрочем, как отмечает M.Сипсер в своем учебнике по теории сложности вычислений, вместо этого лучше говорить " mapping reducibility " (сводимость с помощью отображений), сохраняя букву m в обозначении.
Отметим, что это определение не симметрично относительно перехода к дополнению, если это делается только в одном из множеств: вовсе не обязательно A <=m N \ A, хотя всегда A <=m A.
44.Покажите, что A  N \ A для перечислимого
неразрешимого множества A.
N \ A для перечислимого
неразрешимого множества A.
Отметим, что множества  и N являются
особыми случаями для m -сводимости.
Например, любое разрешимое множество A
сводится к любому множеству B, если только B не
является
пустым и не совпадает с N. В самом деле, если
и N являются
особыми случаями для m -сводимости.
Например, любое разрешимое множество A
сводится к любому множеству B, если только B не
является
пустым и не совпадает с N. В самом деле, если 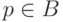 ,
, 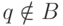 и A разрешимо, то сводящую
функцию можно
построить так:
и A разрешимо, то сводящую
функцию можно
построить так:
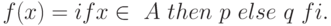
Если же B пусто или совпадает с N, то только пустое множество (соответственно N ) сводится к B.
45. Существует ли множество натуральных чисел, к которому m -сводится любое множество натуральных чисел?
m-полные множества
Теорема 32. Среди перечислимых множеств существуют наибольшие с точки зрения m -сводимости, то есть множества, к которым m -сводится любое перечислимое множество.
Таковым является универсальное множество (формально надо перейти от
пар к их номерам). Пусть 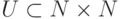 перечислимое множество пар
натуральных чисел, универсальное для класса перечислимых
множеств натуральных чисел. Рассмотрим множество V номеров
всех пар, входящих в U (для какой-то вычислимой нумерации
пар
перечислимое множество пар
натуральных чисел, универсальное для класса перечислимых
множеств натуральных чисел. Рассмотрим множество V номеров
всех пар, входящих в U (для какой-то вычислимой нумерации
пар ![\langle x,y\rangle \hm\leftrightarrow [x,y]\hm\in \bb N$](/sites/default/files/tex_cache/40fb8bf21bdd4be50396dfb0742942e3.png) ).
Другими словами,
).
Другими словами,
![V = \{ [x,y] \mid \langle x,y\rangle \in U\}.](/sites/default/files/tex_cache/d2a29912f6787fb2b7f9a01bc8e6f869.png)
Пусть T произвольное перечислимое множество. Тогда T=Un при некотором n и потому
![x\in T \Leftrightarrow x \in U_n \Leftrightarrow \langle n,x\rangle \in U
\Leftrightarrow [n,x] \in V.](/sites/default/files/tex_cache/a572345f6f2a1d9764b09440607e0f02.png)
Таким образом, функция ![x\hm\mapsto [n,x]](/sites/default/files/tex_cache/150bf8cd44494acc39ae733e41e2ea33.png) сводит T к V.
сводит T к V.
Наибольшие относительно m -сводимости перечислимые множества называют m - полными (точнее, m - полными в классе перечислимых множеств ).
Заметим, что если K <=m A для перечислимых множеств K и A и при этом K является m -полным, то и A является m -полным (в силу транзитивности).
Если универсальное множество является главным, то его диагональ также m -полна:
Теорема 33. Пусть 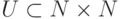 главное универсальное
множество для класса
перечислимых множеств.
Тогда его
" диагональное сечение"
главное универсальное
множество для класса
перечислимых множеств.
Тогда его
" диагональное сечение" 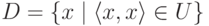 является m -полным.
является m -полным.
(В частности, множество всех самоприменимых программ является m -полным.)
Очевидно, D перечислимо. Пусть K произвольное
перечислимое множество. Рассмотрим перечислимое множество
пар V = K x N. Его сечения Vn будут
либо пусты
(при 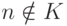 ), либо совпадать со всем N
(при
), либо совпадать со всем N
(при 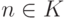 ).
).
Поскольку множество U является главным, существует всюду
определенная функция s, для которой Vn=Us(n).
Другими
словами, Us(n) совпадает с N при 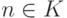 и
пусто при
и
пусто при 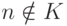 . Следовательно,
. Следовательно,  (и
потому
(и
потому  ) при
) при 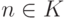 и
и 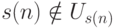 (и
потому
(и
потому 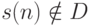 ) при
) при 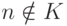 . Таким
образом, s сводит K к D.
. Таким
образом, s сводит K к D.
46. Докажите, что множество всех программ, останавливающихся на входе 0, является m -полным. Докажите, что множество всех программ, останавливающихся хотя бы на одном входе, является m -полным.
47.
Пусть M m -полное перечислимое множество.
Покажите,
что существует алгоритм, который по номеру любой всюду
определенной функции h указывает такое число n,
что 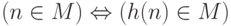 .
(Указание: это утверждение составляет содержание теоремы
о неподвижной точке для некоторого отношения эквивалентности.)
.
(Указание: это утверждение составляет содержание теоремы
о неподвижной точке для некоторого отношения эквивалентности.)
