Свойства главных нумераций

Изоморфизм главных нумераций

Доказанное только что утверждение о получении новых номеров используется при доказательства теоремы Роджерса об изоморфизме главных (геделевых) нумераций. Вот ее формулировка:

Теорема 23. Пусть U₁ и U₂ две главные универсальные функции для класса вычислимых функций одного аргумента. Тогда существуют две всюду определенные взаимно обратные вычислимые функции s₁₂ и s₂₁, для которых

U1(n,x)=U2(s12(n),x) и U2(n,x)=U1(s21(n),x)

при любых n и x.

Эта теорема показывает, что трансляторы, сводящие одну главную нумерацию к другой и наоборот, можно выбрать взаимно обратными, так что любые две главные нумерации отличаются лишь вычислимой перестановкой номеров. (Заметим, что утверждение предыдущей теоремы 22 является следствием теоремы об изоморфизме главных нумераций. В самом деле, для некоторых главных нумераций например, для нумераций, получающихся из языков программирования, есть способы получать сколько угодно новых номеров той же функции, поэтому в силу изоморфизма такой способ есть и для любой другой главной нумерации.)

Мы будем действовать примерно так же, как и при доказательстве изоморфизма счетных плотных всюду упорядоченных множеств без первого и последнего элементов. Построение искомых биекций происходит по шагам. На k -м шаге строится некоторое взаимно однозначное соответствие

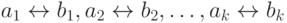
между двумя конечными k -элементными подмножествами натурального ряда. При этом для каждого i числа a_i и b_i являются номерами одной и той же функции, только в разных нумерациях ( a_i относительно U₁, а b_i относительно U₂ ).

На каждом шаге построения мы добавляем новую пару с сохранением указанного свойства. При этом постепенно с обеих сторон мы включим все натуральные числа. Тем самым мы получим искомое взаимно однозначное соответствие, и оно будет вычислимым, раз наша конструкция вычислима.

Итак, как мы добавляем новую пару? На четных шагах мы берем наименьшее натуральное число u, не входящее в левую сторону соответствия (не встречающееся среди a_i ). Оно является U₁ -номером некоторой функции. Поскольку нумерация U₂ главная, мы можем получить некоторый U₂ -номер той же функции. Обозначим его v. Если v не встречается среди b_i, дело сделано: мы добавляем пару к нашему соответствию. Если встречается, мы пользуемся теоремой 22 и получаем другие U₂ -номера той же функции до тех пор, пока среди них не окажется нового, еще не встречавшегося среди b_i.

На нечетных шагах мы действуем аналогичным образом, но начинаем с наименьшего числа, не встречающегося среди b_i.

Замечание для программистов (которое не следует воспринимать серьезно): поскольку, скажем, паскаль и си можно считать главными нумерациями, то по доказанной теореме существуют не просто трансляторы из паскаля в си и наоборот, а взаимно обратные. (Впрочем, основная часть доказательства при этом не используется, поскольку в паскале и си в программу можно добавлять комментарии, получая сколько угодно эквивалентных программ.)

Аналогичная теорема верна и для главных нумераций перечислимых множеств: любые две такие нумерации изоморфны (отличаются вычислимой перестановкой номеров). Доказательство также проводится аналогично; сначала нужно показать, что в главной нумерации по любому номеру можно алгоритмически получить сколько угодно номеров того же множества. При этом применяются два способа один годится для всех множеств, кроме пустого, другой для пустого.

  33. Проведите это рассуждение подробно.