| Казахстан, Алматы |
Свойства главных нумераций
Новые номера старых функций
Теорема Успенского-Райса показывает, что в главной нумерации множество номеров любой конкретной функции неразрешимо и потому бесконечно. Сейчас мы докажем более сильный факт: по номеру любой функции в главной нумерации можно алгоритмически получить сколько угодно других номеров той же функции. Формально это можно выразить, например, так:
Теорема 22. Пусть U главная универсальная функция. Тогда существует всюду определенная функция g двух аргументов с таким свойством: для любого i числа g(i,0),g(i,1),... являются различными U -номерами функции Ui.
План таков: мы построим другую систему программирования, в которой заданная функция Ui имеет бесконечно много программ. Затем, пользуясь тем, что функция U главная, будем " транслировать" эти программы и получать U -номера интересующей нас функции. Конечно, нужны специальные хитрости, чтобы гарантировать, что получится бесконечно много разных номеров: вообще говоря, разные программы после трансляции могут слиться. (Например, если в нашей системе программирования разрешены комментарии, то ничего не стоит найти сколько угодно различных программ для одной и той же функции, добавляя разные комментарии к программе но если транслятор начинает свою работу с удаления комментариев, то ничего хорошего не выйдет.)
Вот как реализуется описанный выше план. Пусть h произвольная функция. Покажем, что существует алгоритм, отыскивающий бесконечно много различных U -номеров функции h. (В теореме утверждается, что это можно сделать не только для конкретной функции h, но и для всех функций Ui, как говорят, " равномерно по i ", но временно забудем про это.)
Пусть P перечислимое неразрешимое множество. Рассмотрим вычислимую функцию

Среди функций Vn встречаются всего две: если 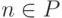 ,
то Vn = h ; если
,
то Vn = h ; если  ,
то Vn нигде не определенная
функция, которую мы обозначим через
,
то Vn нигде не определенная
функция, которую мы обозначим через 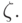 Будем пока считать,
что
Будем пока считать,
что 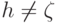 (при
(при  эта конструкция не
работает
и нам потребуется чуть более сложная).
эта конструкция не
работает
и нам потребуется чуть более сложная).
Так как U главная универсальная функция, то существует транслятор s, переводящий V -номера в U -номера. При этом
-
 ;
; -
 .
.
Таким образом, если p(0),p(1),... вычислимое перечисление множества P, то все числа s(p(0)),s(p(1)),... будут U -номерами функции h. Покажем, что среди этих чисел бесконечно много различных (и потому можно вычислять их одно за другим, пока не обнаружится новый, еще не использованный, номер функции h ).
Пусть это не так, и множество  конечно.
Тогда X разрешимо.
Если
конечно.
Тогда X разрешимо.
Если 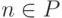 , то
, то  по построению;
если
по построению;
если  ,
то s(n) номер функции
,
то s(n) номер функции  и потому не может
принадлежать X (напомним, что
и потому не может
принадлежать X (напомним, что 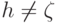 ).
Следовательно,
).
Следовательно, 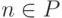 равносильно
равносильно  , и
потому
из разрешимости X следует разрешимость P, что
противоречит
предположению.
, и
потому
из разрешимости X следует разрешимость P, что
противоречит
предположению.
Это рассуждение, однако, не проходит, если функция h
нигде не определена. Хотя числа s(p(0)),s(p(1)),... по-прежнему будут номерами h,
ничто не гарантирует нам, что среди них бесконечно много
различных.
В этом случае
поступим чуть хитрее и рассмотрим любую вычислимую
функцию  отличную от
отличную от  (например,
тождественно
нулевую). Рассмотрим два перечислимых неотделимых множества P и Q и
вычислимую функцию
(например,
тождественно
нулевую). Рассмотрим два перечислимых неотделимых множества P и Q и
вычислимую функцию

Пусть s транслятор, переводящий V -номера в U -номера. Тогда
-
 ;
; -
 ;
; -
 .
.
Как и раньше, числа s(p(0)),s(p(1)),... будут номерами
функции h. Покажем, что если 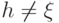 , то
множество X таких чисел
неразрешимо (и потому бесконечно). В самом деле, если X разрешимо, то мы можем отделить P
от Q разрешимым
множеством. Именно, множество
, то
множество X таких чисел
неразрешимо (и потому бесконечно). В самом деле, если X разрешимо, то мы можем отделить P
от Q разрешимым
множеством. Именно, множество  содержит P
(по построению) и не пересекается с Q (поскольку
при
содержит P
(по построению) и не пересекается с Q (поскольку
при 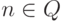 число s(n) будет номером функции
число s(n) будет номером функции  и потому не
может
лежать в X ).
и потому не
может
лежать в X ).
Таким образом, у нас есть две конструкции, позволяющие получать другие номера заданной функции h. Первая из них заведомо годится (дает бесконечно много новых номеров), если h хотя бы где-то определена; вторая заведомо действует для нигде не определенной h. Пусть нам теперь дана функция h и заранее не известно, является ли она нигде не определенной или нет. Что тогда? Тогда можно применять параллельно обе конструкции, пока одна из них не даст нам требуемый новый номер мы знаем, что по крайней мере одна из конструкций обязана сработать, хотя и не знаем, какая.
Это позволяет нам провести рассуждение равномерно по i. Формально говоря, надо действовать так. Рассмотрим две вычислимые функции V1 и V2 двух аргументов, определенные соотношениями
![\begin{align*}
V_1([i,n],x) & =
\left\{
\begin{aligned}
{}&\text{$U(i,x)$}, \text{ если $n\in P$,}\\
{}&\text{не определено}, \text{ если $n\notin P$,}\\
\end{aligned}
\right.\\[1ex]
V_2([i,n],x) & =
\left\{
\begin{aligned}
{}&\text{$U(i,x)$}, \text{ если $n\in P$,}\\
{}&\text{$0$}, \text{ если $n\in Q$,}\\
{}&\text{не определено},\text{ если $n\notin P\cup Q$}\\
\end{aligned}
\right.
\end{align*}](/sites/default/files/tex_cache/4e1695627bdf9b7c80b164b90923a962.png)
( P и Q фиксированные перечислимые неотделимые
множества, [u,v] номер пары 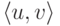 в
фиксированной вычислимой
нумерации пар). Поскольку U главная универсальная функция, можно
найти такие
вычислимые всюду определенные
функции s1 и s2, что V1([i,n],x) = U(s1([i,n]),x)
и V2([i,n],x) = U(s2([i,n]),x).
Пусть p всюду определенная функция одного аргумента, для которой P = {p(0),p(1),...}. Искомую функцию g можно
определить так: g(i,k) есть k -ое (без учета повторений) число в
последовательности
в
фиксированной вычислимой
нумерации пар). Поскольку U главная универсальная функция, можно
найти такие
вычислимые всюду определенные
функции s1 и s2, что V1([i,n],x) = U(s1([i,n]),x)
и V2([i,n],x) = U(s2([i,n]),x).
Пусть p всюду определенная функция одного аргумента, для которой P = {p(0),p(1),...}. Искомую функцию g можно
определить так: g(i,k) есть k -ое (без учета повторений) число в
последовательности
s1([i,p(0)]), s2([i,p(0)]), s1([i,p(1)]), s2([i,p(1)]), s1([i,p(2)]), s2([i,p(2)]),...
