|
По первому тесту выполнил дважды задания. Результат получается правильный (проверял калькулятором). Пишет, что "Задание не проверено" и предлагает повторить. |
Операторы управления
ЗАДАЧА 3.14. Дано натуральное число  . Определить, является ли оно простым. Натуральное число
. Определить, является ли оно простым. Натуральное число  называется простым, если оно делится нацело без остатка только на единицу и
называется простым, если оно делится нацело без остатка только на единицу и  . Число 13 — простое, так как делится только на 1 и 13, N = 12 не является простым, так как делится на 1, 2, 3, 4, 6 и 12.
. Число 13 — простое, так как делится только на 1 и 13, N = 12 не является простым, так как делится на 1, 2, 3, 4, 6 и 12.
Входные данные: N — целое число.
Выходные данные: сообщение.
Промежуточные данные: i — параметр цикла, возможные делители числа N.
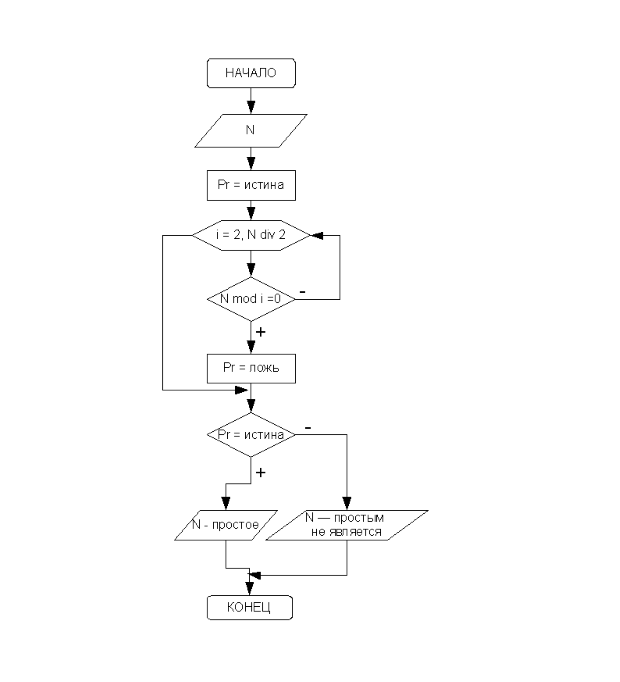
Алгоритм решения этой задачи (рис. 3.33) заключается в том, что необходимо определить, есть ли у числа N делители среди чисел от 2 до N/2. Если делителей нет — число простое. Предположим, что число N является простым (Pr:=true). Организуем цикл, в котором переменная i будет изменяться от 2 до N/2. В цикле будем проверять, делится ли N на i. Если делится, то мы нашли делитель, N не является простым (Pr:=false). Проверка остальных делителей не имеет смысла, аварийно покидаем цикл.
В алгоритме предусмотрено два выхода из цикла. Первый — естественный, при исчерпании всех значений параметра, а второй — досрочный. После выхода из цикла надо проверить значение Pr. Если Pr=true, то число N — простое, иначе N не является простым числом.
При составлении программы на языке Free Pascal досрочный выход из цикла удобно выполнять при помощи оператора break:
var
N, i : integer;
Pr : boolean;
begin
write ( ’N= ’ );
readln (N);
Pr:= true; {Предположим, что число простое.}
for i :=2 to N div 2 do
{Если найдется хотя бы один делитель, то}
if N mod i = 0 then
begin
Pr:= false; {число простым не является и}
break; {досрочный выход из цикла.}
end;
{Проверка значения логического параметра, и}
if Pr then
{вывод на печать соответствующего сообщения.}
writeln ( ’Число ’,N, ’ - простое ’ )
else
writeln ( ’Число ’,N, ’ простым не является ’ );
end.
 до
до  , где
, где  и
и  — натуральные числа, причем
— натуральные числа, причем  .
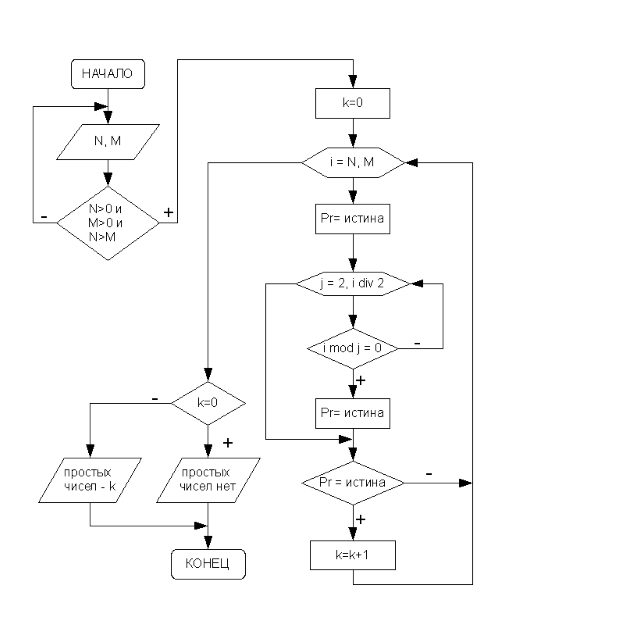
.Алгоритм решения данной задачи представлен на рис. 3.34.
Обратите внимание, что здесь осуществляется проверка корректности ввода исходных данных. Если границы интервала не положительны, или значение N превышает M, ввод данных повторяется в цикле с постусловием до тех пор, пока не будут введены корректные исходные данные. Далее для каждого числа из указанного интервала (параметр i принимает значения от N до M) происходит проверка. Если число является простым, то переменная k увеличивается на единицу. Подробно определение простого числа описано в задаче 3.14.
Программа на языке Free Pascal, реализующая алгоритм подсчёта количества простых чисел в заданном диапазоне:
var N,M, i, j, k : longint;
Pr : boolean;
begin
repeat
write ( ’N= ’ );
readln (N);
write ( ’M= ’ );
readln (M);
until (N>0) and (M>0) and (N<M);
k : = 0; {Количество простых чисел.}
for i :=N to M do {Параметр i принимает значения от N до M.}
begin
{Определение простого числа.}
Pr:= true;
for j :=2 to i div 2 do
if i mod j = 0 then
begin
Pr:= false;
break;
end;
{Если число простое, увеличиваем количество на 1.}
if Pr then
k:=k+1;
end;
if k=0 then writeln ( ’Простых чисел в диапазоне нет ’ )
else writeln ( ’Простых чисел в диапазоне ’, k );
end.
 . Определить количество цифр в числе.
. Определить количество цифр в числе.Входные данные: N — целое число.
Выходные данные: kol — количество цифр в числе.
Промежуточные данные: M — переменная для временного хранения значения N.
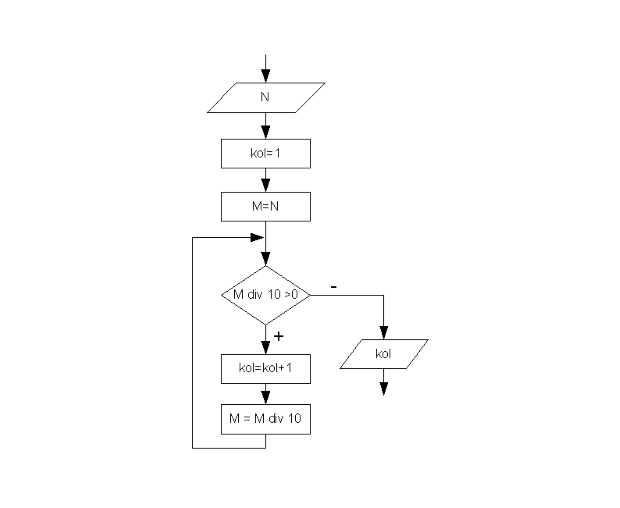
Для того чтобы подсчитать количество цифр в числе, необходимо определить, сколько раз заданное число можно разделить на десять нацело. Например, пусть N=12345, тогда количество цифр kol = 5. Результаты вычислений сведены в таблицу 3.8. Алгоритм определения количества цифр в числе представлен на рис. 3.35.
| kol | N |
|---|---|
| 1 | 12345 |
| 2 | 12345 div 10=1234 |
| 3 | 1234 div 10=123 |
| 4 | 123 div 10=12 |
| 5 | 12 div 10=1 |
| 1 div 10=0 |
Текст программы, реализующей данную задачу, можно записать так:
var
M,N: longint;
kol : word;
begin
{Так как речь идёт о натуральных числах,}
{при вводе предусмотрена проверка.}
{Закончить цикл, если введено положительное число,}
{иначе повторить ввод}
repeat
write ( ’N= ’ );
readln (N);
until N>0;
M:=N; {Сохранить значение переменной N. }
kol : = 1; {Пусть число состоит из одной цифры.}
while M div 10 > 0 do
{Выполнять тело цикла, пока число делится нацело на 10.}
begin
kol := kol +1; {Счётчик количества цифр.}
M:=M div 1 0; {Изменение числа.}
end;
writeln ( ’ kol= ’, kol );
end.
 . Определить, содержит ли это число нули и в каких разрядах они расположены (например, число 1 101 111 011 содержит ноль в третьем и восьмом разрядах).
. Определить, содержит ли это число нули и в каких разрядах они расположены (например, число 1 101 111 011 содержит ноль в третьем и восьмом разрядах).Входные данные: N — целое число.
Выходные данные: pos — позиция цифры в числе.
Промежуточные данные: i — параметр цикла, M — переменная для временного хранения значения N.
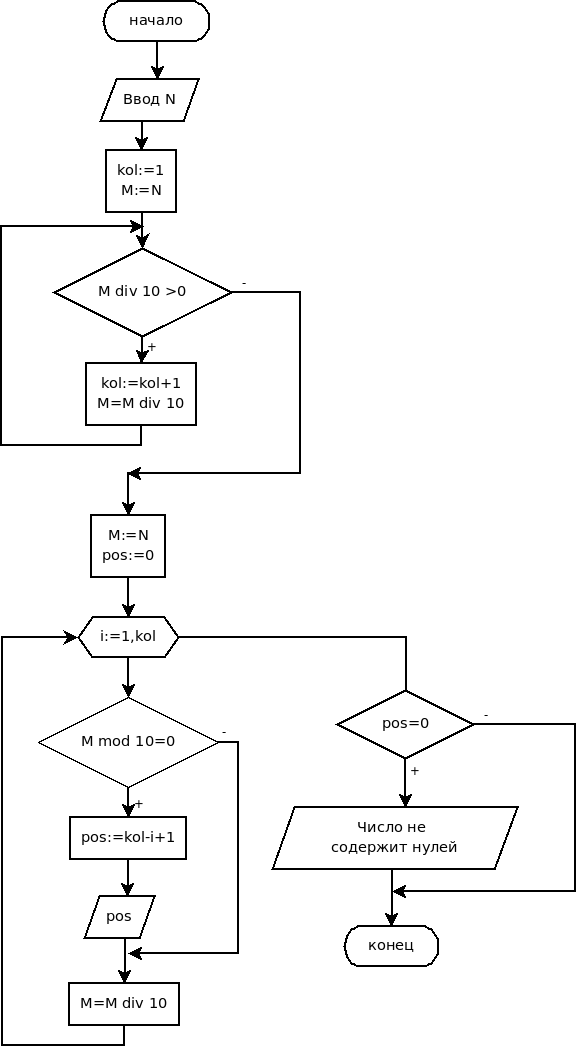
В связи с тем, что разряды в числе выделяются, начиная с последнего, то для определения номера разряда в числе, необходимо знать количество цифр в числе1212Алгоритм нахождения количества цифр в числе был рассмотрен в предыдущей задаче.. Таким образом, на первом этапе решения задачи необходимо определить kol — количество цифр в числе. Затем начинаем выделять из числа цифры; если очередная цифра равна нулю, нужно вывести на экран номер разряда, который занимает эта цифра. Процесс определения текущей цифры числа N=120405 представлен в таблице 3.9.
Блок-схема алгоритма решения данной задачи показана на рис. 3.36.
| i | Число М | Цифра | Номер позиции |
|---|---|---|---|
| 1 | 120405 div 10=12040 | 120405 mod 10=5 | 6 |
| 2 | 12040 div 10=1204 | 12040 mod 10=0 | 5 |
| 3 | 1204 div 10=120 | 1204 mod 10=4 | 4 |
| 4 | 120 div 10=12 | 120 mod 10=0 | 3 |
| 5 | 12 div 10=1 | 12 mod 10=2 | 2 |
| 6 | 1 div 10=0 | 1 mod 10=1 | 1 |
Текст программы, реализующей данный алгоритм:
var
M,N: longint;
i, pos, kol : word;
begin
{Так как речь идет о натуральных числах,}
{при вводе предусмотрена проверка.}
{Закончить цикл, если введено положительное число,}
{иначе повторить ввод}
repeat
write ( ’N= ’ );
readln (N);
until N>0;
//Определение kol - количества разрядов.
M:=N; {Сохранить значение переменной N.}
kol : = 1; {Пусть число состоит из одной цифры.}
while M div 10 > 0 do
{Выполнять тело цикла, пока число делится нацело на 10.}
begin
kol := kol +1; {Счётчик количества цифр.}
M:=M div 1 0; {Изменение числа.}
end;
writeln ( ’ kol= ’, kol );
M:=N;
pos : = 0; {Пусть в числе нет нулей.}
for i :=1 to kol do
begin
{Выделение цифры из числа и сравнение её с нулем.}
if (M mod 10 = 0) then
begin
pos := kol-i +1; {Позиция нуля в числе.}
writeln ( ’Ноль в ’, pos, ’м- разряде. ’ );
end;
M:=M div 1 0; {Изменение числа.}
end;
if pos=0 then writeln ( ’Число не содержит цифру 0. ’ );
end.