|
По первому тесту выполнил дважды задания. Результат получается правильный (проверял калькулятором). Пишет, что "Задание не проверено" и предлагает повторить. |
Операторы управления
3.5.4 Операторы передачи управления
Операторы передачи управления принудительно изменяют порядок выполнения команд. В языке Free Pascal таких операторов пять: goto, break, continue, exit и halt.
Оператор goto метка, где метка — обычный идентификатор, применяют для безусловного перехода, он передаёт управление оператору с меткой.
метка : оператор;
Обычно применение оператора goto приводит к усложнению программы и затрудняет отладку. Использование оператора нарушает принцип структурного программирования11Как говорил учитель программирования авторов книги Владимир Андреевич Реуцкий: "Использование goto — признак дурного тона"., согласно которому все блоки, составляющие программу, должны иметь только один вход и один выход. В большинстве алгоритмов применения оператора goto можно избежать, в нашей книге мы будем его использовать, но читатель должен знать о наличии этого оператора в языке.
Операторы break и continue используют только внутри циклов. Оператор break осуществляет немедленный выход из циклов repeat, while, for, и управление передается оператору, находящемуся непосредственно за циклом. Оператор continue начинает новую итерацию цикла, даже если предыдущая не была завершена.
Оператор exit осуществляет выход из подпрограммы.
Оператор halt прекращает выполнение программы.
3.5.5 Решение задач с использованием циклов
Рассмотрим использование циклических операторов на конкретных примерах.
 и
и  .
.Входные данные: A и B. Выходные данные: А — НОД.
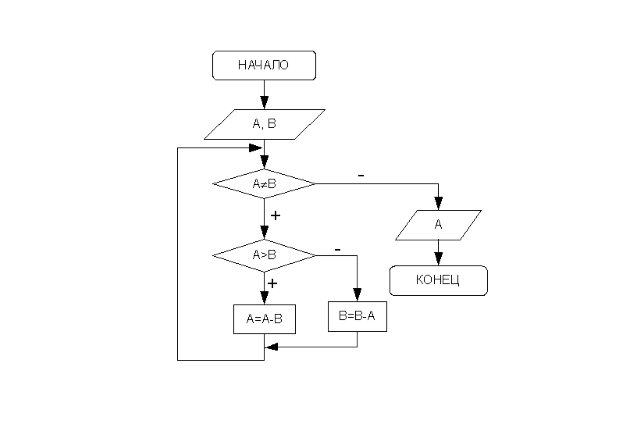
Для решения поставленной задачи воспользуемся алгоритмом Евклида: будем уменьшать каждый раз большее из чисел на величину меньшего до тех пор, пока оба значения не станут равными, так, как показано в таблице 3.4.
В блок-схеме решения задачи, представленной на рис. 3.28, для решения поставленной задачи используется цикл с предусловием, то есть тело цикла повторяется до тех пор, пока А не равно В. Следовательно, при создании программы воспользуемся циклом while..do.
| Исходные данные | Первый шаг | Второй шаг | Третий шаг | НОД(A,B)=5 |
|---|---|---|---|---|
| А=25 | А=10 | А=10 | А=5 | |
| В=15 | В=15 | В=5 | В=5 |
Программа на языке Free Pascal, реализующая поставленную задачу:
var a, b : word;
begin
writeln ( ’введите два натуральных числа ’ );
write ( ’A= ’ ); readln ( a );
write ( ’B= ’ ); readln ( b );
{Если числа не равны, выполнять тело цикла.}
while a<>b do
{Если число А больше, чем В, то уменьшить его значение на В,}
if a>b then
a:=a-b
{иначе уменьшить значение числа В на А.}
else
b:=b-a;
writeln ( ’НОД= ’,A);
end.
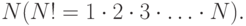 .
.Входные данные: N — целое число, факториал которого необходимо вычислить.
Выходные данные: factorial — значение факториала числа N, произведение чисел от 1 до N, целое число.
Промежуточные переменные: i — параметр цикла, целочисленная переменная, последовательно принимающая значения 2, 3, 4 и так далее до N.
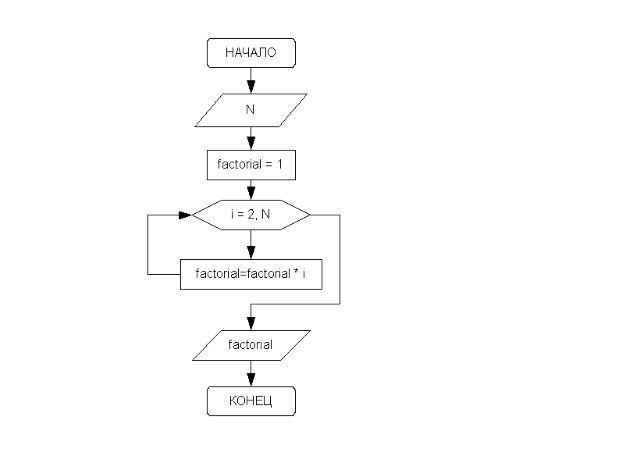
Блок-схема приведена на рис. 3.29.
Итак, вводится число N. Переменной factorial, предназначенной для хранения значения произведения последовательности чисел, присваивается начальное значение, равное единице. Затем организуется цикл, параметром которого выступает переменная i. Если значение параметра цикла меньше или равно N, то выполняется оператор тела цикла, в котором из участка памяти с именем factorial считывается предыдущее значение произведения, умножается на текущее значение параметра цикла, а результат снова помещается в участок памяти с именем factorial. Когда параметр i становится больше N, цикл заканчивается, и на печать выводится значение переменой factorial, которая была вычислена в теле цикла.
Ниже представлен текст программы вычисления факториала на языке Free Pascal.
var factorial, n, i : integer; begin write ( ’ n= ’ ); readln ( n ); factorial : = 1; for i :=2 to n do factorial := factorial * i; writeln ( factorial ); end.
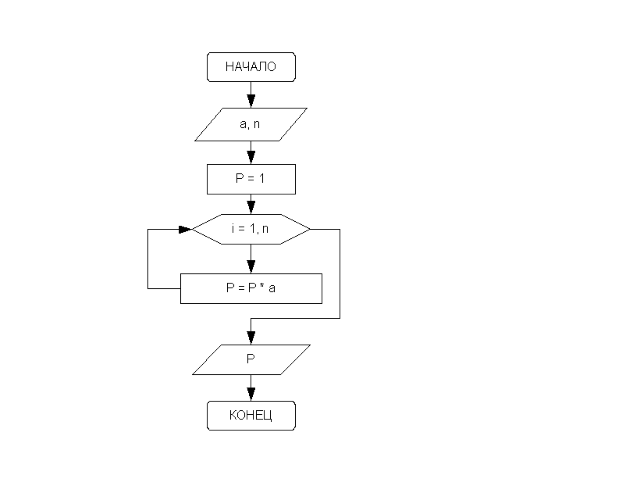
Входные данные: a — вещественное число, которое необходимо возвести в целую положительную степень n. Выходные данные: p (вещественное число) — результат возведения вещественного числа a в целую положительную степень n. Промежуточные данные: i — целочисленная переменная, принимающая значения от 1 до n с шагом 1, параметр цикла. Блок-схема приведена на рис. 3.30.
Известно, что для того, чтобы получить целую степень n числа a, нужно умножить его само на себя n раз. Результат этого умножения будет храниться в участке памяти с именем p. При выполнении очередного цикла из этого участка предыдущее значение будет считываться, умножаться на основание степени a и снова записываться в участок памяти p. Цикл выполняется n раз.
В таблице 3.5 отображён протокол выполнения алгоритма при возведении числа 2 в пятую степень: a=2, n=5. Подобные таблицы, заполненные вручную, используются для тестирования — проверки всех этапов работы программы.
Далее приведён текст программы, составленной для решения поставленной задачи.
var a, p : real; i, n : word; begin write ( ’Введите основание степени a= ’ ); readln ( a ); write ( ’Введите показатель степени n= ’ ); readln ( n ); p : = 1; for i :=1 to n do p:=p * a; writeln ( ’P= ’,P : 1 : 3 ); end.
 .
.Входные данные: N — целое число.
Выходные данные: S — сумма четных чисел.
Промежуточные переменные: i — параметр цикла, принимает значения 2, 4, 6, 8 и так далее, также имеет целочисленное значение.
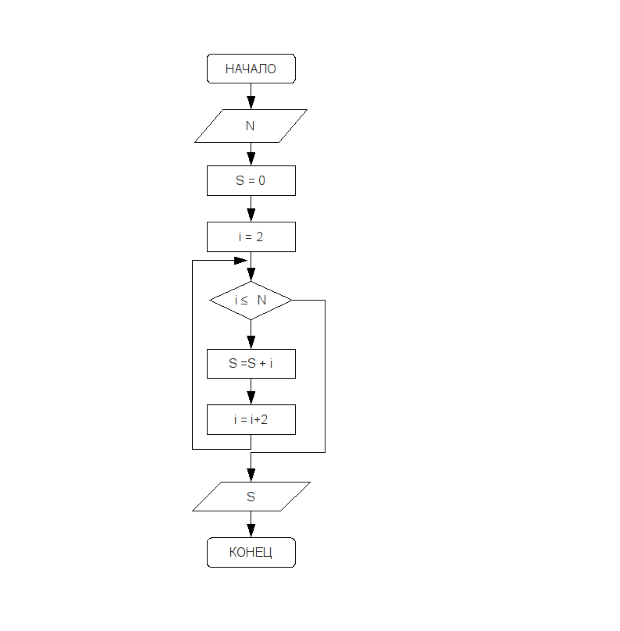
При сложении нескольких чисел необходимо накапливать результат в определённом участке памяти, каждый раз считывая из этого участка предыдущее значение суммы и прибавляя к нему следующее слагаемое. Для выполнения первого оператора накапливания суммы из участка памяти необходимо взять такое число, которое не влияло бы на результат сложения. Перед началом цикла переменной, предназначенной для накапливания суммы, необходимо присвоить значение нуль (s=0). Блок-схема решения этой задачи представлена на рис. 3.31.
Так как параметр цикла i изменяется с шагом 2, в блок-схеме, построенной для решения данной задачи (рис. 3.31), использован цикл с предусловием, который реализуется при составлении программы с помощью оператора while..do:
var n, i, S : word; begin write ( ’ n= ’ ); readln ( n ); S : = 0; i : = 2; while i<=n do begin S:=S+i; i := i +2; end; writeln ( ’ S= ’, S ); end.
Эту же задачу можно решить иначе, используя цикл for..do:
var n, i, S : word;
begin
write ( ’ n= ’ );
readln ( n );
S : = 0;
for i :=1 to n do
{Если остаток от деления параметра цикла на 2 равен 0,}
{то это число четное, следовательно,}
{происходит накапливание суммы.}
if i mod 2 = 0 then
S:=S+i;
writeln ( ’ S= ’, S );
end.
В таблице 3.6 приведены результаты тестирования программы для n=7. Несложно заметить, что при нечётных значениях параметра цикла значение переменной, предназначенной для накапливания суммы, не изменяется.
 . Определить
. Определить  — количество делителей этого числа, меньших его (например, для
— количество делителей этого числа, меньших его (например, для  делители 1, 2, 3, 4, 6. Количество
делители 1, 2, 3, 4, 6. Количество  ).
).Входные данные: N — целое число.
Выходные данные: целое число K — количество делителей N.
Промежуточные переменные: i — параметр цикла, возможные делители числа N.
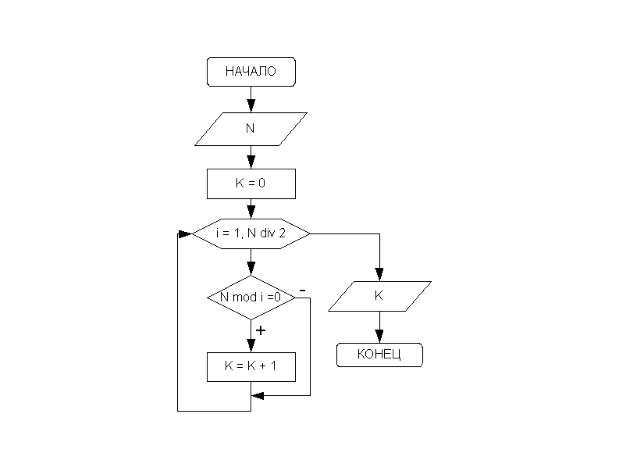
В блок-схеме, изображённой на рис. 3.32, реализован следующий алгоритм: в переменную K, предназначенную для подсчёта количества делителей заданного числа, помещается значение, которое не влияло бы на результат (k=0). Далее организовывается цикл, в котором изменяющийся параметр i выполняет роль возможных делителей числа N. Параметр цикла меняется от 1 до N/2 c шагом 1. Если заданное число делится нацело на параметр цикла, это означает, что i является делителем N, и значение переменной K следует увеличить на единицу. Цикл необходимо повторить N/2 раз.
В таблице 3.7 отображены результаты тестирования алгоритма при определении делителей числа N=12.
Текст программы, соответствующий описанному алгоритму:
var N, i,K: word;
begin
write ( ’N= ’ );
readln (N);
K: = 0;
for i :=1 to N div 2 do
{Если N делится нацело на i, то}
if N mod i= 0 then
k:=K+1; {увеличить счетчик на единицу.}
writeln ( ’ K= ’,K);
end.