|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Потоки в сетях
Сетевой симплексный алгоритм
Время выполнения алгоритма вычеркивания циклов зависит не только от количества циклов отрицательной стоимости, которые используются для снижения стоимости потока, но и от времени поиска каждого такого цикла. В этом разделе мы рассмотрим базовый подход, который не только резко снижает трудоемкость выявления отрицательных циклов, но и позволяет использовать приемы уменьшения количества итераций. Эта реализация алгоритма вычеркивания циклов называется сетевым симплексным (network simplex) алгоритмом. Он основан на использовании древовидной структуры данных и на переназначении стоимостей, что позволяет быстро выявлять отрицательные циклы.
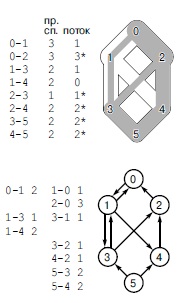
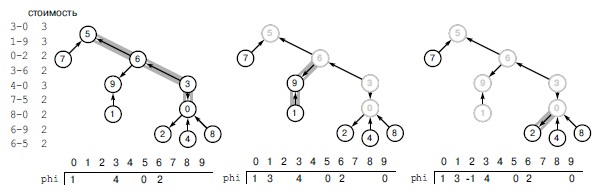
По отношению к любому потоку ребро может быть пустым, полным или частично заполненным (ни пустое, ни полное). В этом потоке ребро 1-4 пусто; ребра 0-2, 2-3, 2-4, 3-5 и 4-5 заполнены, а ребра 0-1 и 1-3 частично заполнены. Наши графические соглашения дают два способа обозначения состояний ребер: в столбце потока цифры 0 означают пустые ребра, звездочки означают заполненные ребра, а остальные ребра - это частично заполненные ребра. В остаточной сети (внизу) пустые ребра появляются только в левом столбце, полные - в правом столбце, а частично заполненные ребра могут находиться в обоих столбцах.
Прежде чем перейти к описанию сетевого симплексного алгоритма, мы заметим, что по отношению к любому потоку каждое ребро u-v сети может находиться в одном из трех состояний (см. рис. 22.43):
- Пустое, поэтому поток можно протолкнуть только из u в v.
- Полное, поэтому поток можно протолкнуть только из v в u.
- Частично заполненное (т.е. ни пустое, ни заполненное), и поток можно проталкивать в обоих направлениях.
С этой классификацией мы уже сталкивались при использовании остаточных сетей в данной главе. Если ребро u-v пустое, то u-v входит в остаточную сеть, а v-u не входит; если ребро u-v заполнено, то v-u входит в остаточную сеть, а u-v не входит; а если ребро u-v заполнено частично, то в остаточную сеть входят и u-v, и v-u .
Определение 22.10. Пусть имеется максимальный поток без циклов из частично заполненных ребер. Тогда допустимым остовным деревом (feasible spanning tree) этого максимального потока является любое остовное дерево сети, которое содержит все частично заполненные ребра.
В этом контексте направления ребер в остовном дереве игнорируются. То есть любое множество V- 1 ориентированных ребер, которые соединяют V вершин сети между собой (без учета направлений ребер), составляет остовное дерево, а остовное дерево допустимо, если все ребра, не входящие в дерево, являются полными или пустыми.
Первый шаг сетевого симплексного алгоритма заключается в построении остовного дерева. Один из способов его построения - вычисление максимального потока, разбиение циклов из частично заполненных ребер (расширение потока, чтобы заполнить или опустошить одно из его ребер), и последующее добавление пустых или полных ребер к остальным частично заполненным ребрам с целью построения остовного дерева. Пример такого процесса показан на рис. 22.44. В другом варианте на первом шаге вычисляется максимальный поток в фиктивном ребре из истока в сток. Затем это ребро является единственно возможным частично заполненным ребром, и мы можем построить остов-ное дерево для данного потока с помощью любого поиска на графе. Пример такого остовного дерева приводится на рис. 22.45.
Добавление в остовное дерево любого недревесного ребра приводит к образованию цикла. Механизм, на котором основан сетевой симплексный алгоритм - это множество весов вершин, которое обеспечивает немедленное выявление тех ребер, которые при включении в остовное дерево создают циклы отрицательной стоимости в остаточной сети. Мы будем называть эти веса вершин потенциалами (potential), а потенциал, связанный с вершиной v, будем обозначать ф(v). В зависимости от контекста мы будем рассматривать потенциал то как функцию, определенную на вершинах, то как множество целочисленных весов (предполагая, что каждой вершине присвоен такой вес), то как вектор, индексированный именами вершин (поскольку в реализациях мы храним их именно в таком виде).
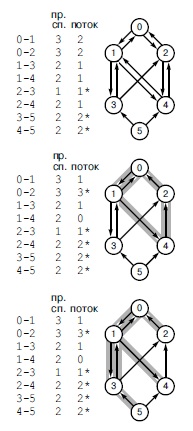
Если имеется максимальный поток (вверху), то с помощью двухэтапного процесса, представленного в данном примере, можно построить максимальный поток с таким остовным деревом, что ни одно из ребер, не включенных в остовное дерево, не является частично заполненным ребром. Сначала мы разрываем циклы из частично заполненных ребер: в данном случае мы разрываем цикл 0-2-4-1-0, проталкивая по нему поток величиной 1. Таким способом всегда можно заполнить или опустошить по крайней мере одно ребро; в данном случае мы опустошаем ребро 1-4 и заполняем ребра 0-2 и 2-4 (в центре). Затем мы включаем пустые и полные ребра в множество частично заполненных ребер, чтобы получить остовное дерево; в данном случае мы добавляем ребра 0-2, 1-4 и 3-5 (внизу).
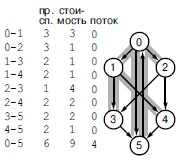
Если начать с потока по фиктивному ребру из истока в сток, то оно оказывается единственно возможным частично заполненным ребром. Поэтому для построения остовного дерева для потока можно использовать любое остовное дерево из остальных ребер. В данном примере ребра 0-5, 0-1, 0-2, 1-3 и 1-4 составляют остовное дерево для исходного максимального потока. Все не включенные в дерево ребра остаются пустыми.
Определение 22.11. Пусть задан поток в транспортной сети со стоимостями ребер, а c(u, v) означает стоимость ребра u-v остаточной сети для этого потока. Для любой функции потенциала ф приведенную стоимость (reduced cost) ребра u-v остаточной сети относительно ф мы будем обозначать как c*(u,v) и определим как значение c(u, v) - (ф (u) - ф(v)).
Иначе говоря, приведенная стоимость каждого ребра есть разность между фактической стоимостью ребра и разностью потенциалов вершин этого ребра. В ситуации распределения товаров потенциал узла имеет физический смысл: если интерпретировать потенциал ф(u) как затраты на приобретение единицы товара в узле u, то полная стоимость c*(u, v) + ф (u) - ф (v) означает затраты на закупку товара в узле u, доставку в v и реализацию товара в v.
Мы будем хранить потенциалы вершин в векторе phi, индексированном именами вершин, и вычислять приведенную стоимость ребра v-w, вычитая из стоимости ребра значение (phi[v] -phi[w]). То есть не нужно где-то хранить приведенную стоимость ребра, поскольку ее очень легко вычислить.
В сетевом симплексном алгоритме мы используем допустимые остовные деревья для определения потенциалов вершин таким образом, чтобы приведенные стоимости ребер с учетом этих потенциалов давали прямую информацию о циклах с отрицательной стоимостью. А именно, мы используем при выполнении алгоритма допустимое остовное дерево и устанавливаем такие значения потенциалов вершин, чтобы все древесные ребра имели нулевую приведенную стоимость.
Лемма 22.25. Будем говорить, что множество потенциалов вершин допустимо (valid) по отношению к остовному дереву, если все древесные ребра имеют нулевую приведенную стоимость. Всем допустимым потенциалам вершин любого остовного дерева соответствуют одинаковые приведенные стоимости каждого ребра сети.
Доказательство. Пусть имеются две различные функции потенциала ф и ф', допустимые по отношению к заданному остовному дереву. Покажем, что они различаются на аддитивную константу, т.е. что ф(u) = ф'(u) + А для всех u и некоторой константы А. Тогда ф(u) - ф(v) = ф'(u) - ф'(v) для всех u и v. Отсюда следует, что для двух функций потенциала все приведенные стоимости одинаковы.
Для любых двух вершин u и v, которые связаны между собой древесным ребром, должно выполняться равенство ф (v) = ф (u) - c (u, v), исходя из следующих соображений. Если u-v - древесное дерево, то ф (v) должна быть равно ф (u) - c (u, v), чтобы приведенная стоимость c (u, v) - ф (u) + ф (v) была равна нулю; если v-u - древесное ребро, то ф (v) должна быть равна ф (u) + c (v, u) = ф (u) - c (u, v), чтобы приведенная стоимость c (v, u) - ф (v) + ф (u) была равна нулю. Аналогичные рассуждения для ф' показывают, что ф'(v) = ф'(u) - c (u, v).
Вычтя из одного равенства другое, находим, что ф(v) - ф'(v) = ф(u) - ф'(u) для любых u и v, соединенных древесным ребром. Обозначив эту разность для любой вершины через А, и применив это равенство к ребрам любого дерева поиска по остовному дереву, получаем 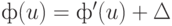 для всех u.
для всех u. 
Есть другой способ представить процесс определения некоторого множества допустимых потенциалов вершин. Сначала мы фиксируем одно значение, потом вычисляем значения для всех вершин, соединенных с исходной вершиной древесными ребрами, затем вычисляем эти значения для всех вершин, соединенных с теми вершинами и т.д. Независимо от того, в какой вершине начат этот процесс, разность потенциалов между любыми двумя вершинами остается одной и той же и определяется только структурой дерева. Пример приведен на рис. 22.46 рис. 22.46. Мы подробно рассмотрим задачу вычисления потенциалов после изучения зависимости между приведенными стоимостями недревесных ребер и циклами отрицательной стоимости.
Лемма 22.26. Назовем недревесное ребро подходящим (eligible), если цикл, создаваемый им с древесными ребрами, является циклом отрицательной стоимости в остаточной сети. Ребро является подходящим тогда и только тогда, когда оно представляет собой полное ребро с положительной приведенной стоимостью или пустое ребро с отрицательной приведенной стоимостью.
Доказательство. Предположим, что ребро u-v создает цикл t1-t2-t3-...-td-t1 с древесными ребрами t1-12, t2-13, ... , где v есть t1 , а u есть td. Определения приведенной стоимости каждого ребра дают следующие равенства:
\begin{align*} c (u, v) &= c^{*}(u, v) +\phi (u) -\phi (t_{1})\\ c(t_{1}, t_{2}) &=\phi (t_{1}) -\phi (t_{2})\\ c (t_{2}, t_{3}) &=\phi (t_{2}) -\phi (t_{3})\\ &\hdots\\ c (t_{d-1}, u) &=\phi(t_{d-1}) -\phi(u) \end{align*}.
Сумма левых частей этих уравнений дает общую стоимость цикла, а сумма правых частей сокращается до c*(u, v). Другими словами, приведенная стоимость ребра дает стоимость цикла, поэтому только описанные ребра могут порождать циклы с отрицательной стоимостью. 
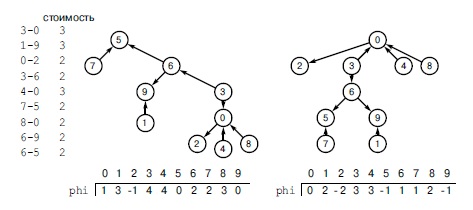
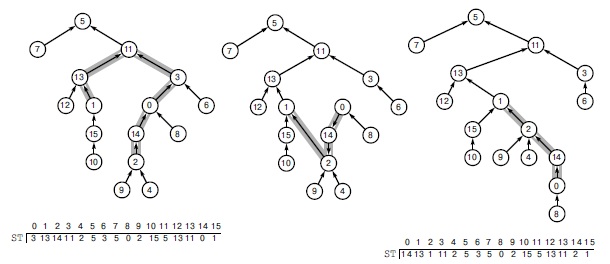
Потенциалы вершин определяются структурой остовного дерева и первоначальным значением потенциала одной любой вершины. Слева приведено множество ребер, которые образуют остовное дерево, состоящее из десяти вершин от 0 до 9. В представлении этого дерева в центре в качестве корня выбрана вершина 5, вершины, соединенные с 5, находятся на уровень ниже и т.д. Присваивание корню нулевого значения потенциала определяет уникальное назначение потенциалов для других узлов, при котором разность потенциалов вершин каждого ребра равна его стоимости. Справа приведено другое представление того же дерева, в котором в качестве корня выбрана вершина 0. После присвоения вершине 0 нулевого значения потенциала будут получены другие потенциалы, которые отличаются от потенциалов на центральной диаграмме на некоторое постоянное значение. Во всех наших вычислениях используется лишь разность потенциалов. Она остается одной и той же для любой пары потенциалов, независимо от начальной вершины (и независимо от присвоенного ей значения) - поэтому выбор исходной вершины и начального значения не играет роли.
Лемма 22.27. Если имеются поток и допустимое остовное дерево, в котором нет подходящих ребер, то поток является потоком минимальной стоимости.
Доказательство. Если подходящие ребра отсутствуют, то в остаточной сети отсутствуют циклы с отрицательной стоимостью, и из условия оптимальности, сформулированного в лемме 22.23, следует, что поток является потоком минимальной стоимости. 
Эквивалентная формулировка утверждает, что если имеются поток и множество потенциалов вершин, такое, что все приведенные стоимости древесных ребер равны нулю, все полные недревесные ребра неотрицательны, а пустые недревесные ребра неположительны, то поток является потоком минимальной стоимости.
При наличии подходящих ребер можно выбрать одно из них и выполнить расширение по циклу, который оно образует с древесными ребрами, чтобы получить поток более низкой стоимости. Аналогично реализации вычеркивания циклов из раздела 22.5, пройдем по циклу, чтобы определить максимальный поток, который можно протолкнуть, а затем еще раз пройдем по циклу, чтобы протолкнуть этот поток, который заполнит или опустошит по меньшей мере одно ребро. Если это подходящее ребро, которое было использовано для построения цикла, оно перестает быть подходящим (его приведенная стоимость не изменяется, но оно превращается из полного в пустое или из пустого в полное). Во всех других случаях оно становится частично заполненным. Присоединение его к дереву и удаление из цикла полного или пустого ребра сохраняет инвариантное условие: никакое недревесное ребро не может быть частично заполненным, а само дерево является допустимым остовным деревом. Как и ранее, мы рассмотрим механику этого вычисления ниже в этом разделе.
Итак, допустимые остовные деревья дают нам потенциалы вершин, которые дают приведенные стоимости, которые дают допустимые ребра, которые дают циклы отрицательной стоимости. Расширение по циклам отрицательной стоимости снижает стоимость потока и заодно мененяет структуру дерева. Из-за изменений в структуре дерева меняются потенциалы вершин, из-за изменений потенциалов вершин меняются приведенные стоимости ребер, а из-за изменений приведенных стоимостей меняется множество подходящих ребер. Выполнив все эти изменения, можно выбрать другое подходящее ребро и начать процесс снова. Эта обобщенная реализация алгоритма вычеркивания циклов для решения задачи о потоке минимальной стоимости и называется сетевым симплексным алгоритмом:
Построим допустимое остовное дерево, используя такие потенциалы вершины, чтобы все вершины дерева имели нулевую приведенную стоимость. Добавим в дерево подходящее ребро, расширим поток в цикле, который оно образует с древесными ребрами, и удалим из дерева ребро, которое оказалось полным или пустым - и будем продолжать этот процесс до тех пор, пока не останется ни одного подходящего ребра.
Это описание является обобщенным, т.к. начальный выбор остовного дерева, способ вычисления потенциалов вершин и выбор подходящих ребер не определены. Стратегия выбора подходящих ребер определяет количество итераций и выбирается с учетом затрат на реализацию различных стратегий такого выбора и на пересчет потенциалов вершин.
Лемма 22.28. Если общий сетевой симплексный алгоритм завершает работу, то он вычисляет поток минимальной стоимости.
Доказательство. Если алгоритм прекращает работу, то это потому, что в остаточной сети не осталось циклов отрицательной стоимости, а согласно лемме 22.23 полученный максималный поток обладает минимальной стоимостью. 
Алгоритм может и не завершить работу - из-за того, что расширение в некотором цикле может заполнять или опустошать сразу несколько ребер, и в дереве могут оставаться ребра, через которые невозможно протолкнуть никакой поток. Если мы не можем протолкнуть поток, то не можем снизить стоимость и можем попасть в бесконечный цикл добавления и удаления ребер в фиксированной последовательности остовных деревьев. Было найдено несколько способов избавиться от этой проблемы; мы рассмотрим их ниже в этом разделе, после того как более подробно рассмотрим реализации.
Первое, с чем нужно определиться при разработке сетевого симплексного алгоритма - это представление остовного дерева. С помощью дерева нам понадобится выполнять следующие действия:
- Вычисление потенциалов вершин.
- Расширение потоков в циклах (и выявление на нем пустых или полных ребер).
- Вставка нового ребра и удаление ребра из полученного цикла.
Каждая из этих задач сама по себе представляет интересное упражнение по разработке структур данных и алгоритмов. Мы могли бы рассмотреть несколько структур данных и множество алгоритмов с различными характеристиками производительности. Вначале мы изучим, пожалуй, простейшую доступную нам структуру данных (с которой мы познакомились еще в "Специальные методы сортировки" ) - это представление дерева родительскими ссылками. Мы рассмотрим алгоритмы и реализации, которые основаны на этом представлении для перечисленных задач и опишем их применение для работы сетевого симплексного алгоритма, а затем обсудим лругие структуры данных и алгоритмы.
Как и в нескольких других реализациях, рассмотренных в данной главе, мы начнем с реализации вычисления максимального пути расширением путей, пользуясь не просто индексами в представлении дерева, а ссылками в сетевое представление, чтобы иметь доступ к значениям потоков, сохраняя доступ и к именам вершин.
Программа 22.10 представляет собой реализацию, которая присваивает потенциалы вершинам за время, пропорциональное V. В ее основе лежит следующая идея (см. рис. 22.47). Мы начинаем с произвольной вершины и рекурсивно вычисляем потенциалы ее предшественников, поднимаясь по родительским ссылкам до самого корня, которому по соглашению присваивается нулевой потенциал. Затем мы выбираем другую вершину и с помощью родительских сссылок рекурсивно вычисляем потенциалы ее предшественников. Рекурсия заканчивается при достижении предшественника с уже известным потенциалом, а затем мы возвращаемся по тому же пути, вычисляя потенциал каждого узла на основе потенциала родительского узла. Этот процесс продолжается до тех пор, пока не будут вычислены все значения потенциалов. Если мы уже прошли по какому-либо пути, то мы больше не посещаем ни одно из его ребер, следовательно, этот процесс выполняется за время, пропорциональное V.
Мы начнем с вершины 0, проходим по пути в корень, обнуляем pt[5], а затем возвращаемся тем же путем назад. В вершине 6 устанавливаем такое значение, чтобы pt[6] - pt[5] было равно стоимости ребра 6-5, затем устанавливаем значение pt[3], чтобы pt[3] - pt[6] было равно стоимости ребра 3-6 и т.д. (слева). После этого мы начинаем с вершины 1 и проходим по родительским ссылкам, пока не встретим вершину с известным потенциалом (в данном случае это 6), и возвращаемся по этому пути, вычислив потенциалы вершин 9 и 1 (в центре). Потом мы начинаем с вершины 2 - мы можем рассчитать ее потенциал из потенциала ее родителя (справа). Перейдя к вершине 3, мы обнаруживаем, что ее потенциал уже известен, и т.д. В данном примере для каждой вершины после 1 мы либо видим, что ее потенциал уже подсчитан, либо можем его вычислить из потенциала ее родителя. Мы никогда не проходим по одному и тому же ребру дважды, независимо от структуры дерева, поэтому общее время этих вычислений линейно.
Программа 22.10. Вычисление потенциалов вершин
Рекурсивная функция phiR поднимается по родительским ссылкам дерева, пока не встретит допустимый потенциал (потенциал корня всегда считается допустимым), а затем вычисляет потенциалы, спускаясь по пройденному пути. Она помечает каждую вершину, потенциал которой вычисляет, текущим значением функции valid.
int phiR(int v)
{ if (mark[v] == valid) return phi[v];
phi[v] = phiR(ST(v)) - st[v]->costRto(v);
mark[v] = valid;
return phi[v];
}
Для двух заданных вершин их ближайший общий предок (БОП, least common ancestor - LCA) определяется как корень минимального поддерева, которое содержит обе эти вершины. Цикл, который образуется при добавлении ребра, соединяющего две вершины, состоит из этого ребра и ребер двух путей, ведущих из двух этих узлов к их БОП. Расширяющий цикл, образованный добавлением ребра v-w, проходит через v-w в w, затем вверх по дереву к БОП вершин v и w (скажем, r), затем вниз по дереву в v. Поэтому на этих двух путях необходимо рассматривать ребра различной ориентации.
Как и раньше, мы расширяем поток в цикле, вначале пройдя по путям, чтобы выявить максимальную величину потока, которую можно протолкнуть через их ребра, а затем еще раз пройдя по этим путям, чтобы протолкнуть через них поток. Не обязательно рассматривать ребра в порядке их расположения в цикле, достаточно просто рассмотреть каждое из них (в любом направлении). Поэтому можно просто пройти каждый путь из этих узлов до их БОП. Чтобы расширить поток в цикле, образованном при добавлении ребра v-w, мы проталкиваем поток из v в w, из v по пути к ближайшему общему предку r и из w по пути до г, но против направления ребер. Программа 22.11 реализует эту идею в виде функции, которая расширяет поток в цикле и заодно возвращает ребро, которое становится пустым или полным из-за этого расширения.
В программе 22.11 используется простая технология, позволяющая избежать затрат на инициализацию всех меток, которую нужно выполнять при каждом вызове программы. Мы храним эти метки как глобальные переменные, которые вначале обнулены. При каждом поиске БОП мы увеличиваем на 1 глобальный счетчик и помечаем вершины, сохраняя в соответствующем элементе вектора, индексированного именами вершин, значение этого счетчика. После инициализации этот метод позволяет выполнять вычисления за время, пропорциональное длине цикла. В типичных задачах расширение может выполняться для множества небольших циклов, поэтому экономия времени может быть весьма существенной. Как мы убедимся далее, этот метод экономии времени можно применять и в других частях реализации.
Программа 22.11. Расширение потока по циклу
Чтобы найти ближайшего общего предка двух вершин, мы синхронно поднимаемся из них по дереву, помечая встреченные узлы. БОП - первый обнаруженный помеченный узел (возможно, корень дерева). Для расширения потока используется функция, похожая на функцию из программы 22.3; она сохраняет пути по дереву в векторе st и возвращает ребро, которое стало при расширении пустым или полным (см. текст).
int lca(int v, int w)
{ mark[v] = ++valid; mark[w] = valid;
while (v != w)
{ if (v != t) v = ST(v);
if (v != t && mark[v] == valid) return v;
mark[v] = valid;
if (w != t) w = ST(w);
if (w != t && mark[w] == valid) return w;
mark[w] = valid;
}
return v;
}
Edge *augment(Edge *x)
{ int v = x->v(), w = x->w(); int r = lca(v, w);
int d = x->capRto(w);
for (int u = w; u ! = r; u = ST(u))
if (st[u]->capRto(ST(u)) < d)
d = st[u]->capRto(ST(u));
for (int u = v; u ! = r; u = ST(u))
if (st[u]->capRto(u) < d)
d = st[u]->capRto(u);
x->addflowRto(w, d); Edge* e = x;
for (int u = w; u ! = r; u = ST(u))
{ st[u]->addflowRto(ST(u), d);
if (st[u]->capRto(ST(u)) == 0) e = st[u];
}
for (int u = v; u ! = r; u = ST(u))
{ st[u]->addflowRto(u, d);
if (st[u]->capRto(u) == 0) e = st[u];
}
return e;
}
Наша третья задача обработки дерева - замена ребра u-v другим ребром в цикле, который образован этим другим ребром с ребрами дерева. В программе 22.12 реализована функция, выполняющая эту задачу для представления родительскими ссылками. Здесь снова играет важную роль БОП вершин u и v, т.к. удаляемое ребро лежит либо на пути из u в БОП, либо на пути из v в БОП. Удаление ребра отсоединяет от дерева всех его потомков, но это можно исправить, обратив направления ссылок между ребром u-v и удаленным ребром, как показано на рис. 22.48.
Эти три реализации позволяют выполнять базовые операции, на которых основан сетевой симплексный алгоритм: (1) выбор подходящего ребра с помощью прсмотра приведенных стоимостей и потоков; (2) расширение потока в отрицательном цикле, образованном ребрами дерева и выбранным подходящим ребром, пользуясь представлением родительскими ссылками для остовного дерева; и (3) изменение дерева и пересчет потенциалов. Эти операции показаны на примере транспортной сети на рис. 22.49 и рис. 22.50.
На рис. 22.49 показана инициализация структур данных с помощью фиктивного ребра с максимальным потоком в нем, как и на рис. 22.42. На нем показано исходное допустимое остовное дерево, представленное родительскими ссылками, соответствующие потенциалы вершин, приведенные стоимости недревесных ребер и исходное множество подходящих ребер.
Этот пример демонстрирует базовые операции с деревом в сетевом симплексном алгоритме для представления родительскими ссылками. Слева изображено дерево, в котором все ссылки направлены вверх, что показывает вектор родительских ссылок ST. (В нашем коде функция ST вычисляет родителя заданной вершины по указателю на ребро, хранящемуся в векторе st, индексированном именами вершин.) Добавление ребра 1-2 образует цикл, в который входят пути из вершин 1 и 2 к их БОП - вершине 11. После удаления одного из этих ребер, скажем, 0-3, структура остается древовидной. Чтобы отразить это изменение в массиве родительских ссылок, мы меняем направления всех ссылок от 2 до 3 (в центре). Дерево справа - то же самое дерево, в котором позиции узлов изменены так, чтобы все ссылки были направлены вверх в соответствии со значениями массива родительских ссылок, представляющего рассматриваемое дерево (справа внизу).
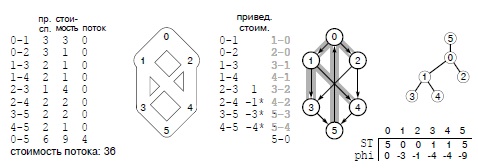
Чтобы выполнить инициализацию структур данных для сетевого симплексного алгоритма, мы начинаем с нулевого потока во всех ребрах (слева), затем добавляем фиктивное ребро 0-5 из истока в сток, величина потока в котором не меньше величины максимального потока (здесь для ясности мы используем значение, равное величине максимального потока). Стоимость 9 фиктивного ребра больше стоимости любого цикла сети; в этой реализации используется значение CV. Фиктивное ребро в транспортной сети не показано, однако включено в остаточную сеть (в центре). Остовное дерево формируется из стока в качестве корня, истока в качестве его единственного потомка, и дерева поиска на графе, индуцированном остальными узлами остаточной сети. Эта реализация использует представление дерева родительскими ссылками в массиве st и функцию ST. На наших рисунках изображена эта реализация и две других: реализация с корнем, показанная справа, и множество заштрихованных ребер в остаточной сети.
Потенциалы вершин содержатся в массиве pt и вычисляются на основе структуры дерева таким образом, чтобы разность потенциалов вершин каждого древесного ребра была равна его стоимости.
В столбце " привед. стоим. " (в центре) показаны приведенные стоимости недревесных ребер, которые вычислены для каждого ребра сложением разности потенциалов вершин и его стоимости. Приведенные цены древесных ребер равны нулю и в столбце не указаны. Пустые ребра с отрицательными приведенными стоимостями и полные ребра с положительными приведенными стоимостями (подходящие ребра) отмечены звездочками.
Программа 22.12. Замена остовного дерева
Функция update добавляет ребро в остовное дерево и удаляет из образовавшегося при этом цикла некоторое ребро. Удаляемое ребро находится на пути из одной из вершин добавленного ребра к их БОП. Эта реализация использует функцию onpath для поиска удаляемого ребра и функцию reverse для изменения направления ребра на пути между данным и добавляемым ребром.
bool onpath(int a, int b, int c)
{ for (int i = a; i ! = c; i = ST(i))
if (i == b) return true;
return false;
}
void reverse(int u, int x)
{ Edge *e = st[u];
for (int i = ST(u); i != x; i = ST(i))
{ Edge *y = st[i]; st[i] = e; e = y; }
}
void update(Edge *w, Edge *y)
{ int u = y->w(), v = y->v(), x = w->w ();
if (st[x] != w) x = w->v();
int r = lca(u, v);
if (onpath(u, x, r))
{ reverse(u, x); st[u] = y; return; }
if (onpath(v, x, r))
{ reverse(v, x); st[v] = y; return; }
}
Вместо вычисления величины максимального потока в реализации используется величина оттока из истока, которая гарантированно не меньше величины максимального потока; в данном случае используется величина максимального потока, чтобы было легче проследить работу алгоритма.
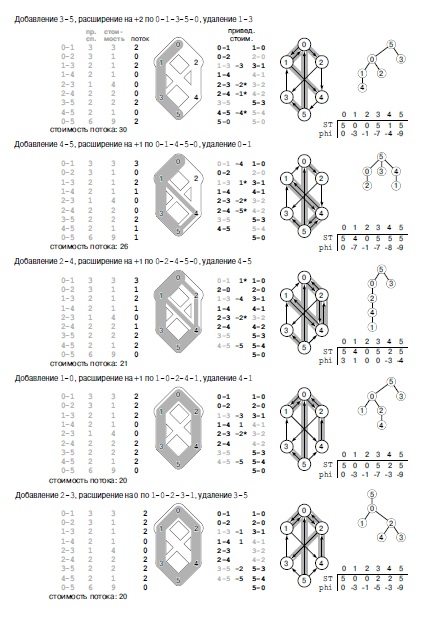
Каждый ряд этого рисунка соответствует одной итерации сетевого симплексного алгоритма после инициализации, представленной на рис. 22.49. На каждой итерации алгоритм выбирает подходящее ребро, расширяет поток по циклу и изменяет структуры данных следующим образом. Сначала выполняется расширение потока, включая соответствующие изменения в остаточной сети. После этого в древовидную структуру ST добавляется подходящее ребро, и из цикла, которое оно образует с ребрами дерева, удаляется ребро. Потом изменения в структуре дерева отображаются в таблице потенциалов phi. Затем изменяются приведенные стоимости недревесных ребер (столбец " привед. стоим. " в центре), чтобы отобразить изменения значений потенциалов, и эти значения используются для выявления пустых ребер с отрицательной приведенной стоимостью и полных ребер с положительной приведенной стоимостью как подходящих ребер (помечены звездочками около приведенных стоимостей). Реализации не обязательно должны выполнять именно такие вычисления (они просто должны вычислить изменения потенциалов и приведенных стоимостей, чего достаточно для выявления подходящих ребер), однако мы приводим здесь все числа, чтобы дать полное представление об алгоритме.
Последнее расширение в этом примере вырождено. Оно не увеличивает поток, но и не выявляет подходящих ребер - это гарантирует, что данный поток является максимальным потоком минимальной стоимости.
На рис. 22.50 показаны изменения в структурах данных для каждой последовательности подходящих ребер и расширения потока по циклам отрицательной стоимости. Эта последовательность не отражает какой-либо конкретный метод выбора подходящих ребер; в ней представлены решения, которые делают расширяющие пути такими, как на рис. 22.42. На этих рисунках изображены все потенциалы вершин и все приведенные стоимости после каждого цикла расширения, даже если многие из этих значений определены неявно и не обязательно должны вычисляться типовыми реализациями. Эти рисунки демонстрируют общее продвижение алгоритма и состояние структур данных при переходах алгоритма от одного допустимого остовного дерева к другому, когда в дерево добавляется подходящее ребро и из образовавшегося цикла удаляется одно из ребер.
Один из критических фактов, представленных на рис. 22.50, заключается в том, что алгоритм может просто не завершить работу, т.к. пустые или полные ребра остовного дерева могут помешать протолкнуть поток по найденному отрицательному циклу. То есть можно найти походящее ребро и отрицательный цикл, который оно образует с ребрами остовного дерева, но максимальная величина потока, которую можно протолкнуть через этот цикл, может оказаться равной 0. В этом случае мы заменим подходящим ребром одно из ребер цикла, однако снизить стоимость потока не удастся. Чтобы алгоритм завершал свою работу, необходимо сделать так, чтобы алгоритм не начал выполнять бесконечную последовательность расширений потока на нулевую величину.
Если расширяющий цикл содержит более одного полного или пустого ребра, то подстановка алгоритма из программы 22.12 всегда удаляет из дерева то ребро, которое расположено ближе других к БОП двух вершин подходящего ребра. К счастью, доказано, что такая стратегия выбора ребра для удаления из цикла обеспечивает завершение работы алгоритма (см. раздел ссылок).
И последний выбор, который нам придется сделать при разработке реализации сетевого симплексного алгоритма - это стратегия выявления подходящих ребер и выбора одного из них для включения в дерево. Нужна ли специальная структура данных для хранения подходящих ребер? Если нужна, то насколько сложная? Ответ на эти вопросы в какой-то степени зависит от приложения и динамических характеристик решения конкретных задач. Если общее количество подходящих ребер невелико, то лучше использовать специальную структуру данных, а если большая часть ребер обычно являются подходящими, то такая структура не нужна. Дополнительная структура данных позволяет снизить затраты на поиск подходящих ребер, но может также потребовать выполнения трудоемких операций по обновлению данных. Каков критерий выбора нужного подходящего ребра? Как обычно, у нас богатый выбор.
Мы рассмотрим примеры в наших реализациях, а затем исследуем возможные альтернативы. Например, программа 22.13 содержит функцию, которая находит подходящее ребро минимальной приведенной стоимости: никакое другое ребро не дает цикл, расширение потока по которому приведет к большему снижению суммарной стоимости.
Программа 22.14 представляет собой полную реализацию сетевого симплексного алгоритма, которая использует стратегию выбора подходящего ребра, дающего отрицательный цикл с максимальным абсолютным значением стоимости. Эта реализация использует функции работы с деревьями и поиск подходящих ребер из программ 22.10-22.13, но здесь применимо замечание к нашей первой реализации вычеркивания циклов (программа 22.9): удивительно, что такой небольшой кодовый фрагмент позволяет получать полезные решения в контексте общей модели решения задач о потоках минимальной стоимости.
Программа 22.13. Поиск подходящих ребер
Данная функция находит подходящее ребро минимальной приведенной стоимости. Эта примитивная реализация выполняет обход всех ребер в сети.
int costR(Edge *e, int v)
{ int R = e->cost() + phi[e->w()] - phi[e->v()];
return e->from(v) ? R : -R;
}
Edge *besteligible()
{ Edge *x = 0;
for (int v = 0, min = C*G.V(); v < G.V(); v++)
{ typename Graph::adjIterator A(G, v);
for (Edge* e = A.beg(); !A.end(); e = A.nxt())
if (e->capRto(e->other(v)) > 0)
if (e->capRto(v) == 0) if (costR(e, v) < min)
{ x = e; min = costR(e, v) ; }
}
return x;
}
Граница производительности в худшем случае для программы 22.14 по меньшей мере в V раз меньше, чем граница для реализации с вычеркиванием циклов из программы 22.9, т.к. время, необходимое на одну итерацию, равно просто E (чтобы найти подходящее ребро), а не VE (чтобы найти отрицательный цикл). Можно подумать, что применение максимального расширения приведет к меньшему количеству расширений, чем выбор первого попавшегося отрицательного цикла, который находит алгоритм Беллмана-Форда, однако этот способ ничего не улучшает. Конкретные границы количества расширяющих циклов трудно вычислить, и обычно эти границы намного выше, чем величины, которые наблюдаются на практике. Как уже было сказано, имеются теоретические результаты, показывающие, что некоторые стратегии гарантируют, что количество расширяющих циклов ограничено полиномом от количества ребер, хотя в практических реализациях обычно используются варианты с экспоненциальным худшим случаем.
В свете всех этих соображений существует множество возможностей для повышения производительности рассматриваемых алгоритмов. Например, еще одна реализация сетевого симплексного алгоритма приведена в программе 22.15. Примитивная реализация в программе 22.14 всегда требует времени, пропорционального V, на обновление потенциалов дерева, и всегда тратит время, пропорциональное E, на поиск подходящего ребра с максимальной приведенной стоимостью. Реализация в программе 22.15 ликвидирует эти затраты в типичных сетях.
Во-первых, даже если выбор максимального ребра приводит к меньшему количеству итераций, затраты на проверку каждого ребра при поиске максимального ребра могут оказаться излишними. За время, необходимое на просмотр всех ребер, можно выполнить много расширений потоков по коротким циклам. Поэтому имеет смысл рассмотреть стратегию использования произвольного подходящего ребра, а не тратить время на поиск какого-то особенного.
Программа 22.14. Сетевой симплексный алгоритм (базовая реализация)
Данный класс использует сетевой симплексный алгоритм для решения задачи о потоке минимальной стоимости. Он использует стандартную функцию поиска в глубину dfsR на исходном дереве (см. упражнение 22.117), затем входит в цикл, в котором использует функции из программ 22.10-22.13 для вычисления потенциалов всех вершин, просмотра всех ребер и отыскания такого, которое образует отрицательный цикл минимальной стоимости, и расширения потока по этому циклу.
template <class Graph, class Edge>
class MINCOST
{ const Graph &G; int s, t; int valid;
vector<Edge *> st; vector<int> mark, phi;
void dfsR(Edge);
int ST(int);
int phiR(int);
int lca(int, int); Edge *augment(Edge *);
bool onpath(int, int, int);
void reverse(int, int);
void update(Edge *, Edge *);
int costR(Edge *, int); Edge *besteligible();
public:
MINCOST(Graph &G, int s, int t) : G(G), s(s), t(t)
st(G.V()), mark(G.V(), -1), phi(G.V())
{ Edge *z = new EDGE(s, t, M*G.V(), C*G.V());
G.insert(z);
z->addflowto(t, z->cap());
dfsR(z);
for (valid = 1; ; valid++ )
{ phi[t] = z->costRto(s); mark[t] = valid;
for (int v = 0; v < G.V(); v++)
if (v != t) phi[v] = phiR(v);
Edge *x = besteligible();
if (costR(x, x->v()) == 0) break;
update(augment(x), x);
}
G.remove(z); delete z;
}
Программа 22.15. Сетевой симплексный алгоритм (улучшенная реализация)
Замена ссылок на phi обращениями к phiR в функции R и замена цикла for в конструкторе программы 22.14 данным кодом дает реализацию сетевого симплексного алгоритма, которая экономит время на каждой итерации, вычисляя потенциалы только когда это необходимо, и выбирая первое обнаруженное подходящее ребро.
int old = 0;
for (valid = 1; valid != old; )
{ old = valid;
for (int v = 0; v < G.V(); v++)
{ typename Graph::adjIterator A(G, v);
for (Edge* e = A.beg(); !A.end(); e = A.nxt())
if (e->capRto(e->other(v)) > 0)
if (e->capRto(v) == 0)
{ update(augment(e), e); valid++; }
}
}
В худшем случае при поиске подходящего ребра придется проверить все ребра или их большую часть, но обычно нужно проверить сравнительно небольшое количество ребер, чтобы отыскать подходящее. Один из подходов - каждый раз начинать все с начала; другой подход - случайный выбор исходной точки (см. упражнение 22.126). Такое использование случайности делает маловероятным появление неестественно длинных последовательностей расширяющих путей.
Во-вторых, для вычисления потенциалов мы принимаем " отложенный " подход. Вместо того чтобы вычислять все потенциалы в векторе phi, индексированном именами вершин, а потом выбирать их по мере необходимости, мы вызываем функцию phiR, чтобы получить каждое значение потенциала; она поднимается по дереву до обнаружения допустимого потенциала, а затем вычисляет все необходимые потенциалы на этом пути. Чтобы реализовать такой подход, мы просто заменяем обращение к массиву phi[u] на вызов функции phiR(u). В худшем случае мы вычисляем все потенциалы так же, как и раньше, однако при просмотре лишь нескольких подходящих ребер мы вычисляем только те потенциалы, которые необходимы для выявления этих ребер.
Такие изменения никак не влияют на производительность алгоритма в худшем случае, но они, несомненно, ускоряют его работу в реальных ситуациях. Несколько других соображений по повышению производительности сетевого симплексного алгоритма анализируются в упражнениях (см. упражнения 22.i26-22.i30), и это лишь незначительная часть того, что было предложено.
Как мы неоднократно подчеркивали в этой книге, задача анализа и сравнения алгоритмов на графах сложна сама по себе. С появлением сетевого симплексного алгоритма эта задача еще больше усложнилась из-за различных подходов к реализации и большого разнообразия приложений, с которыми нам приходится сталкиваться (см. раздел 22.5). Какая из реализаций лучше? Стоит ли сравнивать реализации по известным границам для худших случаев? Насколько точно можно выразить различие в производительности различных реализаций для конкретных приложений? Следует ли использовать различные реализации, приспособленные для конкретных случаев?
Мы рекомендуем читателям поэкспериментировать с различными реализациями сетевого симплексного алгоритма и найти ответы на некоторые из предложенных вопросов, проведя эмпирические исследования, подобные тем, которые мы настоятельно рекомендовали на протяжении всей книги. При поиске решения задач о потоке минимальной стоимости мы сталкиваемся со знакомыми фундаментальными проблемами, но опыт, приобретенный при решении все более трудных задач на протяжении этой книги, сформирует у вас солидный фундамент для разработки эффективных реализаций, которые способны эффективно решать широкий спектр важных практических задач. Некоторые из этих исследований описаны в упражнениях в конце этого и следующего разделов, но эти упражнения следует рассматривать только как отправную точку. Каждый читатель может провести свои эмпирические исследования, которые проливают свет на некоторые интересные моменты реализаций и/или приложений.
Возможность существенно повысить производительность критических приложений за счет правильного использования классических структур данных и алгоритмов (либо разработки новых) для базовых задач делает изучение реализаций сетевого симплексного алгоритма благодатной областью исследований (поэтому существует обширная литература по его реализациям). Когда-то прогресс в этой области произвел настоящий переворот, т.к. помог снизить огромные затраты на решение сетевых симплексных задач. Пользователи предпочитают решать такие задачи с помощью тщательно отлаженных библиотек, и это оправдано во многих случаях. Однако таким библиотекам трудно постоянно соответствовать современным исследованиям и приспосабливаться к задачам, которые возникают в новых ситуациях. Быстродействие и размеры современных компьютеров, а также доступные реализации наподобие программ 22.12 и 22.13 могут послужить отправными точками для разработки эффективных средств решения задач для многочисленных приложений.
Упражнения
22.116. Приведите максимальный поток с соответствующим допустимым остовным деревом для транспортной сети с рис. 22.10.
22.117. Реализуйте функцию dfsR для программы 22.14.
22.118. Реализуйте функцию, которая удаляет циклы из частично заполненных ребер из потока заданной сети и строит допустимое остовное дерево для полученного потока, как показано на рис. 22.44. Оформите созданную функцию так, чтобы ее можно было использовать для построения исходного дерева в программе 22.14 или в программе 22.15.
22.119. Покажите, как изменятся таблицы потенциалов на рис. 22.46 при изменении ориентации ребра, соединяющего вершины 6 и 5.
22.120. Постройте транспортную сеть и приведите такую последовательность расширяющих ребер, что обобщенный сетевой симплексный алгоритм не остановится.
22.121. Покажите в стиле рис. 22.47 процесс вычисления потенциалов для дерева с корнем в вершине 0 с рис. 22.46.
22.122. Покажите в стиле рис. 22.50 процесс вычисления максимального потока минимальной стоимости в транспортной сети с рис. 22.10, начав с базового максимального потока и связанного с ним базового остовного дерева, которые найдены в упражнении 22.116.
22.123. Пусть все недревесные ребра пусты. Напишите функцию, которая вычисляет потоки в древесных ребрах и помещает поток в ребро, соединяющее вершину v с ее родителем в дереве, в v-й элемент вектора flow.
22.124. Выполните упражнение 22.123 для случая, когда некоторые недревесные ребра могут быть полными.
22.125. Воспользуйтесь программой 22.12 в качестве основы для алгоритма построения MST-дерева. Эмпирически сравните полученную реализацию с тремя базовыми алгоритмами вычисления MST из главы 20 "Минимальные остовные деревья" (см. упражнение 20.66).
22.126. Опишите, что нужно изменить в программе 22.15, чтобы она каждый раз начинала поиск подходящего ребра со случайно выбранного ребра, а не с самого начала.
22.127. Измените решение упражнения 22.126, чтобы каждый поиск подходящего ребра программа начинала с того места, где был завершен предыдущий поиск.
22.128. Измените приватные функции-члены из данного раздела, чтобы использовать трехсвязную древовидную структуру со ссылками на родительский узел, самый первый дочерний узел и следующий сестринский узел (см. "Рекурсия и деревья" ). Функции расширения потока по циклу и замены ребра в дереве подходящим ребром должны выполняться за время, пропорциональное длине расширяющего цикла, а функция вычисления потенциалов должна выполняться за время, пропорциональное размеру меньшего из двух поддеревьев, образованных при удалении древесного ребра.
22.129. Измените приватные функции-члены из данного раздела, чтобы они, кроме базового вектора родительских ребер в дереве, использовали бы два других вектора, индексированных именами вершин: один содержит расстояние от каждой вершины до корня, а другой - потомка каждой вершины в дереве DFS. Функции расширения потока по циклу и замены ребра в дереве подходящим ребром должны выполняться за время, пропорциональное длине расширяющего цикла, а функция вычисления потенциалов должна выполняться за время, пропорциональное размеру меньшего из двух поддеревьев, образованных при удалении древесного ребра.
22.130. Обдумайте идею использования обобщенной очереди подходящих ребер. Рассмотрите различные реализации обобщенной очереди и различные усовершенствования, позволяющие снизить трудоемкость вычислений стоимостей ребер - например, рассматривать только подмножество подходящих ребер, чтобы ограничить размер очереди, или, может быть, позволить некоторым не подходящим ребрам оставаться в очереди.
22.131. Эмпирически определите количество итераций, количество вычислений потенциалов вершин и отношение времени выполнения к E для нескольких версий сетевого симплексного алгоритма и для различных видов сетей (см. упражнения 22.7-22.12). Рассмотрите различные алгоритмы, описанные в тексте и в предыдущих упражнениях, уделяя особое внимание тем, которые лучше работают на больших разреженных сетях.
22.132. Напишите клиентскую программу для графической анимации динамики сетевых симплексных алгоритмов. Эта программа должна создавать изображения, подобные рис. 22.50 и другим рисункам из этого раздела ( рис. 22.48). Протестируйте полученную реализацию на евклидовых сетях из упражнений 22.7-22.12.