|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Минимальные остовные деревья
Алгоритм Прима и поиск по приоритету
Алгоритм Прима, похоже, наиболее прост для реализации из всех алгоритмов поиска MST и рекомендуется для насыщенных графов. В нем используется сечение графа, состоящее из древесных вершин (выбранных для MST) и недревесных вершин (еще не выбранных в MST-дерево). Вначале мы выбираем в качестве MST-дерева произвольную вершину, затем помещаем в MST минимальное перекрестное ребро (которое превращает недревесную вершину MST-дерева в древесную) и повторяем эту же операцию V— 1 раз, пока все вершины не окажутся в дереве.
Из этого описания непосредственно следует примитивная реализация алгоритма Прима. Чтобы найти очередное ребро для включения в MST, необходимо просмотреть все ребра, которые выходят из древесной вершины в недревесную вершину, а затем выбрать из них самое короткое и включить его в MST. Мы не будем рассматривать соответствующую программную реализацию из-за ее крайней неэффективности (см. упражнения 20.35—20.37). Этот алгоритм можно упростить и ускорить с помощью простых структур данных, позволяющих устранить повторные вычисления.
Единичным шагом в алгоритме Прима является добавление вершины в MST-дерево, и прежде чем приступать к реализации, стоит хорошенько разобраться в его сути. Здесь главное — найти кратчайшее расстояние от каждой недревесной вершины до дерева. При присоединении вершины v к дереву единственным возможным изменением для недревесных вершин w является приближение w к дереву. То есть не нужно проверять расстояние от вершины w до всех вершин дерева: достаточно знать минимальное расстояние в каждый момент и проверять, изменяет ли добавление вершины v в дерево это минимальное расстояние.
Для реализации этой идеи нам потребуются такие структуры данных, которые предоставляют следующую информацию:
- Ребра дерева.
- Самое короткое дерево, соединяющее недревесную вершину с деревом.
- Длина этого ребра.
Простейшей реализацией каждой из этих структур данных будет вектор, индексированный именами вершин (этот вектор можно использовать для хранения древесных ребер, выполняя индексацию по вершинам при их добавлении в дерево). Программа 20.6 представляет собой реализацию алгоритма Прима для насыщенных графов. Она использует для этих трех структур данных векторы mst, fr и wt.
После включения в дерево нового ребра (и вершины) нужно выполнить еще две задачи:
- Проверить, приблизит ли добавление нового ребра какую-либо из недревесных вершин к дереву.
- Найти следующее ребро для включения в дерево.
Реализация в программе 20.6 решает обе эти задачи с помощью одного просмотра недревесных вершин. Сначала она обновляет содержимое векторов wt[w] и fr[w], если v-w приближает w к дереву, после чего изменяется текущий минимум, если wt[w] (длина fr[w]) показывает, что w ближе к дереву, чем любая другая недревесная вершина с меньшим индексом.
Программа 20.6. Алгоритм Прима, реализующий построение MST-дерева
Данная реализация алгоритма Прима рекомендуется для работы с насыщенными графами и может применяться для любого представления графа, в котором возможна проверка существования указанного ребра. Внешний цикл наращивает MST-дерево, выбирая минимальные ребра, которые пересекают сечение между вершинами, входящими в MST, и вершинами, не входящими в него. Цикл по w отыскивает минимальное ребро, сохраняя (если w не содержится в MST) условие, что ребро fr[w] является самым коротким (с весом wt[w]) ребром из w в MST
Результатом вычислений является вектор указателей на ребра. Первый указатель (mst[0]) не используется, остальные (от mst[1] до mst[G.V()]) содержат MST-дерево связного компонента графа, которому принадлежит вершина 0.
template <class Graph, class Edge>
class MST
{ const Graph &G;
vector<double> wt;
vector<Edge *> fr, mst;
public:
MST(const Graph &G) : G(G),
mst(G.V()), wt(G.V(), G.V()), fr(G.V())
{ int min = -1;
for (int v = 0; min != 0; v = min)
{ min = 0;
for (int w = 1; w < G.V(); w++)
if (mst[w] == 0)
{ double P; Edge* e = G.edge(v, w);
if (e)
if ((P = e->wt()) < wt[w])
{ wt[w] = P; fr[w] = e; }
if (wt[w] < wt[min]) min = w;
}
if (min) mst[min] = fr[min];
}
}
void show()
{ for (int v = 1; v < G.V(); v++)
if (mst[v]) mst[v]->show();
}
};
Лемма 20.6. Алгоритм Прима позволяет найти MST для насыщенного графа за линейное время.
Доказательство. Анализ программы 20.6 показывает, что время ее выполнения пропорционально V2 и поэтому линейно для случаев насыщенных графов. 
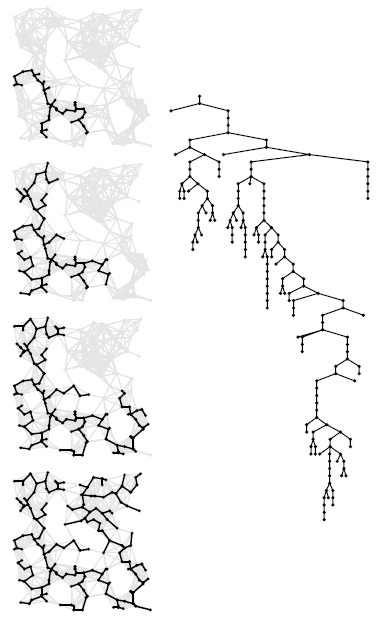
На рис. 20.8 показан пример построения MST-дерева с помощью алгоритма Прима, а на рис. 20.9 показано развертывание MST для более крупного графа.
Программа 20.6 основана на следующем наблюдении: можно чередовать операции поиска минимального ребра и обновления в одном цикле, в котором просматриваются все недревесные ребра. В насыщенных графах количество ребер, которые, возможно, придется просмотреть для обновления расстояния от недревесных вершин до дерева, пропорционально V.
Первым шагом вычисления MST-дерева по алгоритму Прима в это дерево заносится вершина 0. Затем мы находим все ребра, которые соединяют 0 с другими вершинами (еще не включенными в это дерево), и выбираем из них самое короткое (слева вверху). Ребра, соединяющие древесные вершины с недревесными (накопитель), заштрихованы и перечислены под каждым чертежом графа. Для простоты ребра из накопителя перечисляются в порядке возрастания их длины, то есть самое короткое ребро — первое в этом списке. В различных реализациях алгоритма Прима используются различные структуры данных для хранения этого списка и определения минимального ребра. Вторым шагом самое короткое ребро 0-2 переносится (вместе с его конечной вершиной) из накопителя в дерево (вторая диаграмма сверху слева). На третьем шаге ребро 0-7 переносится из накопителя в дерево, в накопителеребро 0-1 заменяется на 7-1, ребро 0-6 на 7-6 (поскольку включение вершины 7 в дерево приближает к дереву вершины 1 и 6), а ребро 7-4 заносится в накопитель (поскольку добавление вершины 7 в дерево превращает 7-4 в ребро, которое соединяет древесную вершину с недревесной) (третья диаграмма сверху слева). Далее, мы переносим в дерево ребро 7-1 (слева внизу). В завершение вычислений мы исключаем из очереди ребра 7-6, 7-4, 4-3 и 3-5, обновляя накопитель после каждой вставки для отражения обнаруженных более коротких или новых путей (справа, сверху вниз).
Ориентированный чертеж растущего MST показан справа от каждого чертежа графа. Ориентация является следствием алгоритма: само MST-дерево обычно рассматривается как неупорядоченное множество неориентированных ребер.
Эта последовательность демонстрирует рост MST-дерева при обнаружении алгоритмом Прима 1/4, 1/2, 3/4 и всех ребер MST-дерева (сверху вниз). Ориентированное представление полного MST-дерева показано справа.
Поэтому поиск ближайшего к дереву недревесного ребра не слишком трудоемок. Но в разреженном графе для выполнения каждой из этих операций может понадобиться значительно менее V шагов. Самое главное при этом — множество ребер-кандидатов для включения в MST, которое мы называем накопителем (fringe). Количество ребер в накопителе обычно существенно меньше количества недревесных ребер, поэтому можно скорректировать описание алгоритма следующим образом. Начинаем с петли исходной вершины в накопителе и до тех пор, пока накопитель не опустеет, выполняем следующие операции:
Переносим минимальное ребро из накопителя в дерево. Посещаем вершину, в которую оно ведет, и помещаем в накопитель все ребра, которые ведут из этой вершины в одну из недревесных вершин, отбрасывая ребро большей длины, если два ребра в накопителе указывают на одну и ту же вершину.
Из этой формулировки ясно, что алгоритм Прима есть ни что иное, как обобщенный поиск на графе (см. "Поиск на графе" ), в котором накопитель представлен очередью с приоритетами на основе операции извлечь минимальное (см. "Очереди с приоритетами и пирамидальная сортировка" . Мы будем называть обобщенный поиск на графе с очередями с приоритетами поиском по приоритету (priority-first search — PFS). Если в качестве приоритетов использовать веса ребер, то поиск по приоритету реализует алгоритм Прима.
Эта формулировка учитывает важное замечание, которое мы сделали выше в "Поиск на графе" в связи с реализацией поиска в ширину. Еще более простой общий подход — просто хранить все ребра, инцидентные древесным вершинам дерева, чтобы механизм очереди с приоритетами находил самое короткое ребро и игнорировал более длинные (см. упражнение 20.41). Как мы убедились в случае поиска в ширину, этот подход неудобен тем, что структура данных накопителя без необходимости загромождается ребрами, которые никогда не попадут в MST. Размер накопителя может возрасти пропорционально E (вместе с затратами на содержание накопителя такого размера), в то время как поиск по приоритету гарантирует, что накопитель не будет содержать более V вершин.
Как и в случае реализации общего алгоритма, имеется целый ряд возможных подходов для взаимодействия с АТД очереди с приоритетами. Один из подходов использует очередь с приоритетами для ребер так же, как в обобщенном поиске на графах из программы 18.10. Реализация в программе 20.7 по существу эквивалентна программе 18.10, но ориентирована на работу с вершинами, чтобы использовать индексированную очередь с приоритетами (см. "Очереди с приоритетами и пирамидальная сортировка" ). (Полная реализация конкретного интерфейса очереди с приоритетами, используемого программой 20.7, приведена в программе 20.10 в конце данной главы.) Будем называть краевыми вершинами (fringe vertex) подмножество недревесных вершин, которые соединены ребрами из накопителя с вершинами дерева, и будем использовать те же векторы, индексированные именами вершин — mst, fr и wt — которые применялись в программе 20.6. Очередь с приоритетами содержит индекс каждой краевой вершины, а этот элемент очереди обеспечивает доступ к самому короткому ребру, соединяющему краевую вершину с деревом и содержит длину этого ребра (во втором и третьем векторах).
Первый вызов функции pfs (поиск по приоритету) в конструкторе программы 20.7 находит MST в связном компоненте, содержащем вершину 0, а последующие вызовы находят MST в других связных компонентах. Таким образом, в не связных графах этот класс фактически находит минимальные остовные леса (см. упражнение 20.34).
Лемма 20.7. Реализация алгоритма Прима с поиском по приоритету, в котором для реализации очереди с приоритетами применяется пирамидальное дерево, позволяет вычислить MST за время, пропорциональное E lg V.
Доказательство. Этот алгоритм напрямую реализует обобщенную идею алгоритма Прима (каждый раз добавлять в MST-дерево минимальное ребро, которое соединяет вершину из MST с вершиной, не входящей в MST). Каждая операция очереди с приоритетами требует выполнения менее lgV шагов. Каждая вершина выбирается операцией извлечь минимальное; в худшем случае каждое ребро может потребовать выполнения операции изменить приоритет.