Орграфы и DAG-графы

Программа 19.1. Обращение орграфа

Данная функция добавляет ребра орграфа, переданного в первом аргументе, в орграф, указанный во втором аргументе. Она использует два спецификатора шаблона, поэтому графы могут иметь различные представления.

  template <class inGraph, class outGraph>
  void reverse(const inGraph &G, outGraph &R)
    { for (int v = 0; v < G.V(); v++)
        { typename inGraph::adjIterator A(G, v);
          for (int w = A. beg() ; !A.end() ;
            w = A.nxt())
          R.insert(Edge(w, v));
        }
    }
      

В орграфах, по аналогии с неориентированными графами, мы говорим об ориентированных циклах (ориентированные пути, ведущие от вершины к ней самой) и о простых ориентированных путях и циклах (в которых все вершины и ребра различны). Обратите внимание, что в орграфе возможен цикл s-t-s длиной 2, но циклы в неориентированных графах должны содержать минимум три различных вершины. Во многих приложениях орграфы не должны содержать циклы, и мы имеем дело с другим видом комбинаторного объекта.

DAG-графы могут встретиться, например, в приложениях, где орграфы моделируют отношения предшествования. DAG-графы естественно возникают не только в этих и других важных приложениях, но и при изучении структур орграфов общего вида. Пример DAG-графа показан на рис. 19.6.

Рис. 19.6. Ориентированный ациклический граф (DAG-граф)

В этом графе нет циклов, хотя это не очевидно ни из списка ребер, ни даже из чертежа графа.

Направленные циклы крайне важны для понимания связности орграфов, не являющихся DAG-графами. Неориентированный граф связен, если существует путь из каждой его вершины в любую другую вершину; но для орграфов используется несколько другое определение:

Рис. 19.7. Терминология орграфов

На подобных чертежах орграфов легко обнаружить истоки (вершины, в которые не ведет ни одно ребро) и стоки (вершины, из которых не выходит ни одно ребро), однако направленные циклы и сильно связные компоненты обнаружить намного труднее. Где самый длинный направленный цикл в данном орграфе?Сколько в нем сильно связных компонентов с более чем одной вершиной?

Граф, изображенный на рис. 19.1, не является сильно связным, поскольку в нем нет, например, ориентированных путей из вершины 9 через вершину 12 к любым другим вершинам графа.

Определение сильно означает, что каждая пара вершин связана более сильным отношением, чем достижимость. Мы говорим, что вершины s и t любого графа является сильно связанными (strongly connected), или взаимно достижимыми (mutually reachable), если существует ориентированный путь из s в t и ориентированный путь из t в s. (Из нашего соглашения, что каждая вершина достижима из самой себя, следует, что каждая вершина сильно связана сама с собой.) Орграф сильно связен тогда и только тогда, когда сильно связаны все его пары вершин. То есть сильно связные орграфы определяет свойство, само собой разумеющееся в случае связных неориентированных графов: если существует путь из s в t, то существует и путь из t в s.

В случае неориентированных графов это свойство выполняется автоматически: один и тот же путь, пройденный в обратном направлении, отвечает всем требованиям определения, но в случае орграфа это уже будет другой путь.

О сильной связности пары вершин можно сказать и по-другому: они принадлежат некоторому ориентированному циклическому пути. Напомним, что мы используем термин циклический путь (cyclic path), а не просто цикл (cycle), чтобы показать, что путь не обязательно должен быть простым. Например, на рис. 19.1 вершины 5 и 6 сильно связаны, поскольку вершина 6 достижима из вершины 5 по ориентированному пути 5-4-2-0-6, а 5 достижима из 6 по ориентированному пути 6-4-3-5. Из существования этих путей следует, что вершины 5 и 6 принадлежат ориентированному циклическому пути 5-4-2-0-6-4-3-5, но не принадлежат никакому (простому) ориентированному циклу. Понятно, что ни один DAG-граф, содержащий более одной вершины, не может быть сильно связным.

Как и простая связность в неориентированных графах, это отношение транзитивно: если s сильно связана с t, а t сильно связана с u, то s сильно связана с u. Сильная связность является отношением эквивалентности, разбивающим вершины графа на классы эквивалентности, в каждом из которых вершины сильно связаны друг с другом. (Отношения эквивалентности подробно рассматриваются в разделе 19.4). Опять-таки, сильная связность в орграфах — свойство, само собой разумеющееся при наличии связности в неориентированных графах.

Например, орграф, который состоит из единого направленного цикла, содержит в точности один сильный компонент. Но ведь и каждая вершина в DAG-графе — это сильный компонент, поэтому каждое ребро в DAG-графе ведет из одного компонента в другой. В общем случае не все ребра орграфа принадлежат сильным компонентам. Это отличается от ситуации для связных компонентов в неориентированных графах — в них каждая вершина, а также каждое ребро принадлежит некоторому связному компоненту — но аналогично ситуации для реберно-связных компонентов в неориентированных графах. Сильные компоненты в орграфах соединены между собой ребрами, которые ведут из вершины одного компонента в вершину другого без обратных ребер.

На рис.19.8 показаны сильные компоненты и коренной DAG-граф для некоторого орграфа. Мы рассмотрим алгоритмы поиска сильных компонентов и построения коренных DAG-графов в разделе 19.6.

Рис. 19.8. Сильные компоненты и коренной DAG

Рассматриваемый орграф (вверху) состоит из четырех сильных компонентов, которые определяются массивом id (в центре), индексированным именами вершин (в качестве индексов взяты произвольные целые числа). Компонент 0 содержит вершины 9, 10, 11 и 12; компонент 1 состоит из единственной вершины 1; компонент 2 содержит вершины 0 , 2 , 3, 4, 5 и 6, а компонент 3 состоит из вершин 7 и 8. Если начертить граф, определяемый ребрами между различными компонентами, то получится DAG-граф (внизу).

Из этих определений, лемм и примеров ясно, что нужно быть предельно точным при использовании путей в орграфе. Необходимо рассмотреть, по меньшей мере, три следующих ситуации:

Связность. Термин связный мы оставим для неориентированных графов. В случае орграфов можно говорить, что две вершины связаны, если они связаны в неориентированном графе, полученном при игнорировании направления ребер, но мы постараемся избегать такой трактовки.

Достижимость. Мы говорим, что вершина t орграфа достижима из вершины s, если существует ориентированный путь из s в t. При работе с неориентированными графами мы постараемся не употреблять термин достижимый (reachable), хотя его можно считать эквивалентным понятию связный, поскольку идея достижимости одной вершины из другой интуитивно понятна в некоторых неориентированных графах (в частности, в графах, представляющих лабиринты).

Сильная связность. Две вершины орграфа сильно связаны, если они взаимно достижимы; в неориентированных графах из связности двух вершин следует существование путей из одной вершины в другую. Сильная связность в орграфах в некоторых отношениях подобна реберной связности в неориентированных графах.

Нам потребуется поддержка операций АТД орграфа, которые принимают в качестве аргументов две вершины s и t и позволяют проверить

• достижима ли t из s;
• являются ли s и t сильно связными (взаимно достижимыми).

Какие ресурсы мы готовы выделить для выполнения этих операций? Как было показано в разделе 17.5 "Виды графов и их свойства" , простое решение задачи связности в неориентированных графах обеспечивалось поиском в глубину. При этом требовалось время, пропорциональное V, но при готовности выполнить предварительную обработку за время, пропорциональное V + E, и выделить объем памяти, пропорциональный V, можно отвечать на запросы о связности графа за постоянное время. Ниже в этой главе мы изучим алгоритмы выявления сильной связности, которые имеют такие же характеристики производительности.

Однако главная трудность в том, что ответы на запросы о достижимости в орграфах получить намного сложнее, чем на запросы о связности или сильной связности. В этой главе мы изучим классические алгоритмы, для выполнения которых требуется время, пропорциональное VE, и объем памяти, пропорциональный V², разработаем реализации с постоянным временем и линейным расходом памяти и времени на предварительную обработку при запросах о достижимости на орграфах определенного типа, и рассмотрим трудности достижения этой оптимальной производительности для всех орграфов.

Упражнения

19.10. Приведите структуру списков смежности, построенных программой 17.9 для орграфа

3-71-47-80-55-23-82-90-64-92-66-4.

19.11. Напишите программу, генерирующую случайные разреженные орграфы для указанного набора значений Vи E, чтобы использовать их для адекватных эмпирических тестов на орграфах, построенных на основе модели со случайными ребрами.

19.12. Напишите программу, генерирующую случайные разреженные орграфы для указанного набора значений V и E, чтобы использовать их для адекватных эмпирических тестов на графах, построенных на основе модели со случайными ребрами.

19.13. Напишите программу, которая генерирует орграфы, соединяя вершины, расположенные на решетке 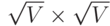, с соседними вершинами случайно направленными ребрами (см. рис. 19.3).

19.14. Добавьте в программу из упражнения 19.13 возможность добавления R дополнительных случайных ребер (все возможные ребра выбираются с равной вероятностью). Для больших значений R сожмите решетку так, чтобы общее количество ребер оставалось примерно равным V. Протестируйте полученную программу, как описано в упражнении 19.11.

19.15. Измените программу из упражнения 19.14, чтобы каждое дополнительное ребро из вершины s в вершину t появлялось с вероятностью, обратно пропорциональной евклидову расстоянию между s и t.

19.16. Напишите программу, которая генерирует в единичном интервале V случайных интервалов длиной d каждый, после чего строит орграф с ребром из интервала s в интервал t тогда и только тогда, когда хотя бы одна из граничных точек s попадает в t (см. упражнение 17.75). Определите, как выбрать d, чтобы ожидаемое количество ребер было равно E. Протестируйте свою программу, как описано в упражнении 19.11 (для разреженных орграфов) или в упражнении 19.12 (для насыщенных орграфов).

19.17. Напишите программу, которая выбирает V вершин и E ребер из реального орграфа, найденного в упражнении 19.1. Протестируйте свою программу, как описано в упражнении 19.11 (для разреженных орграфов) или 19.12 (для насыщенных орграфов).

19.18. Напишите программу, которая с одинаковой вероятностью строит любой из возможных орграфов с V вершинами и с E ребрами (см. упражнение 17.70). Протестируйте свою программу, как описано в упражнении 19.11 (для разреженных орграфов) или 19.12 (для насыщенных орграфов).

19.19. Реализуйте класс, который предоставляет клиентам возможность определять степени захода и выхода любой заданной вершины орграфа за постоянное время после предварительной обработки в конструкторе за линейное время. Затем добавьте функции-члены, которые возвращают за постоянное время количество истоков и стоков.

19.20. Воспользуйтесь программой из упражнения 19.19, чтобы найти среднее количество истоков и стоков в различных видах орграфов (см. упражнения 19.11—19.18).

19.21. Покажите структуру списков смежности, которая получится при построении обращения орграфа

3-71-47-80-55-23-82-90-64-92-66-4

с помощью программы 19.1.

19.22. Опишите обращение отображения.

19.23. Разработайте класс орграфа, который предоставляет клиентам возможность обращаться как к орграфам, так и к их обращениям, и напишите реализацию для любого представления, которое поддерживает запросы к функции edge.

19.24. Напишите альтернативную реализацию класса из упражнения 19.23, которая поддерживает обе ориентации ребер в списках смежности.

19.25. Опишите семейство сильно связных орграфов с V вершинами без (простых) направленных циклов длиной больше 2.

19.26. Приведите сильные компоненты и коренной DAG для орграфа

3-71-47-80-55-23-82-90-64-92-66-4.

19.27. Приведите коренной DAG решетчатого орграфа с рис. 19.3.

19.28. Сколько графов имеют V вершин, каждая из которых имеет степень выхода, равную k?

19.29. Каково ожидаемое количество различных представлений случайного орграфа списками смежности? Указание. Разделите общее количество возможных представлений на общее количество орграфов.