|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Виды графов и их свойства
Программа 17.17. Гамильтонов путь
Данная рекурсивная функция отличается от функции из программы 17.16 всего лишь двумя моментами, во-первых, она принимает длину искомого пути в качестве третьего аргумента и завершается успешно, только если находит путь длины V; во-вторых, при неудачном завершении она сбрасывает маркер visited.
Если заменить этой функцией рекурсивную функцию в программе 17.16 и добавить третий аргумент G.V()-1 в вызов функции searchR, то будет найден гамильтонов путь. Однако не рассчитывайте, что поиск завершится для любых графов, кроме самых маленьких (см. текст).
bool searchR(int v, int w, int d)
{ if (v == w) return (d == 0) ;
visited[v] = true;
typename Graph::adjIterator A(G, v);
for (int t = A.beg(); !A.end(); t = A.nxt())
if (!visited[t])
if (searchR(t, w, d-1)) return true;
visited[v] = false;
return false;
}
Если невозможно найти простой путь из t в w, то это значит, что простого пути из v в w, проходящего через t, не существует; но в процессе поиска гамильтонова пути ситуация иная. Может случиться так, что в графе нет гамильтонова пути в вершину w, который начинается с ребра v-t, но есть путь, который начинается с v-x-t для некоторой вершины x. И придется выполнить рекурсивные вызовы из t, соответствующие каждому пути, который ведет в нее из вершины v. Короче говоря, нам может понадобиться проверить каждый путь в графе.
Задумайтесь, насколько медленно работает алгоритм с факториальным временем выполнения. Если, к примеру, граф с 15 вершинами можно обработать за 1 секунду, то обработка графа с 19 вершинами будет длиться целые сутки, более года для 21 вершины и 6 столетий, если граф содержит 23 вершины. Увеличение быстродействия компьютера практически не помогает. Если повысить быстродействие компьютера в 200 000 раз, то для решения рассматриваемой задачи с 23 вершинами ему потребуется больше суток. Но затраты на обработку графа со 100 или 1000 неимоверно велики, не говоря уже о графах, с которыми нам приходится сталкиваться на практике. Потребуются многие миллионы страниц этой книги, чтобы только записать количество веков, необходимых для обработки графа, содержащего миллионы вершин.
В "Рекурсия и деревья" был рассмотрен ряд простых рекурсивных программ, которые похожи на программу 17.17, но производительность которых можно существенно повысить с помощью нисходящего динамического программирования. Однако данная рекурсивная программа полностью отличается от них по своему характеру: количество промежуточных результатов, которые требуется сохранять в памяти, экспоненциально. Несмотря на громадные усилия многих исследователей, которые пытались решить эту задачу, никто не смог найти алгоритм, который обеспечивал бы приемлемую производительность при обработке графов больших (и даже средних) размеров.
Теперь предположим, что мы изменили начальные условия, и требование обязательного обхода всех вершин заменено на требование обхода всех ребер. Является ли эта задача такой же легкой, как и поиск простого пути, или безнадежно трудной, как поиск гамильтонова пути?
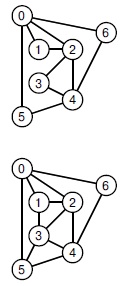
Граф в верхней части рисунка содержит эйлеров цикл 0-1-2-0-6-4-3-2-4-5-0 , который использует все ребра в точности один раз. Граф в нижней части рисунка не содержит такого цикла, однако содержит эйлеров путь 1-2-0-1-3-4-2-3-5-4-6-0-5.
Эйлеров путь. Существует ли путь, соединяющий две заданных вершины, который проходит точно один раз через каждое ребро графа? Путь не обязательно должен быть простым, и вершины можно посещать многократно. Если путь начинается и заканчивается в одной и той же вершине, то это задача поиска эйлерова цикла (Euler tour). Существует ли циклический путь, который проходит через каждое ребро графа в точности один раз? В следствии из леммы 17.4 будет показано, что задача поиска такого пути эквивалентна задаче поиска цикла в графе, полученного добавлением в граф ребра, соединяющего две соответствующие вершины. Два небольших примера приведены на рис. 17.20.
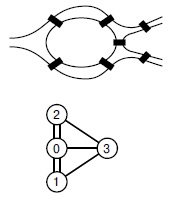
Первым эту классическую задачу исследовал Л.Эйлер (L. Euler) в 1736 г. Некоторые математики считают, что начало изучению графов и теории графов положила работа Эйлера по решению одного из случаев этой проблемы -задачи о Кенигсбергских мостах (см. рис. 17.21). В немецком городе Кенигсберг (с 1946 г. -Калининград, входящий в состав России) берега реки и острова соединяли семь мостов, и жители этого города обнаружили, что они не могут пройти по всем семи мостам, не пройдя по одному из них дважды. Отсюда и берет начало задача поиска эйлерова цикла.
Широко известная задача, которую изучал Эйлер, связана с городом Кенигсберг, где на разветвлении реки Прегель находится остров, соединенный с берегами семью мостами (вверху). Существует ли способ пройти семь мостов во время непрерывной прогулки по городу, не проходя ни по одному из них дважды? Если обозначить остров цифрой 0, берега реки -цифрами 1 и 2, а промежуток между рукавами реки -цифрой 3 и определить ребра, соответствующие каждому мосту, то получится мультиграф, показанный внизу. Требуется найти такой путь, который использует каждое ребро точно один раз.
Подобные задачи знакомы любителям головоломок. Обычно нужно вычертить заданную фигуру, не отрывая карандаша от бумаги, возможно, при условии, что закончить линию нужно там, где она начата. Задача поиска эйлеровых путей естественно возникает при разработке алгоритмов обработки графов, поскольку эйлеровы пути являются эффективным представлением графа (упорядочение ребер графа определенным образом), на основе которых можно разрабатывать эффективные алгоритмы.
Эйлер нашел легкий способ определить, существует ли такой путь -для этого достаточно определить степень каждой вершины. Это свойство нетрудно сформулировать и применять, однако его доказательство в теории графов довольно хитроумно.
Лемма 17.4. Граф содержит эйлеров цикл тогда и только тогда, когда он связен и все его вершины имеют четную степень.
Доказательство. Для упрощения доказательства мы допустим существование петель и параллельных ребер, хотя доказательство нетрудно изменить так, чтобы показать, что эта лемма справедлива и для простых графов (см. упражнение 17.94).
Если в графе имеется эйлеров цикл, то он должен быть связным, поскольку этот цикл определяет путь, соединяющий каждую пару вершин. Кроме того, степень любой вершины графа v должна быть четной, поскольку при обходе цикла (начало которого может быть в любой вершине) мы входим в эту вершину через одно ребро и выходим из нее через другое ребро (ни то, ни другое больше в цикл не входят); следовательно, количество ребер, инцидентных вершине v, должно быть равно удвоенному количеству посещений вершины v при обходе эйлерова цикла, т.е. должно быть равно четному числу.
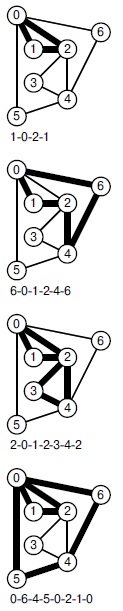
Чтобы доказать достаточность, воспользуемся методом индукции по количеству ребер. Это утверждение заведомо выполняется для графов, у которых нет ребер. Рассмотрим любой связный граф с более чем одним ребром, в котором степени всех вершин четные. Предположим, что начиная с произвольной вершины, мы продвигаемся по любому ребру, после чего удаляем его. Мы продолжаем двигаться, пока не окажемся в вершине, у которой нет ребер. Этот процесс должен когда-нибудь завершиться, поскольку на каждом шаге удаляется одно ребро, но что получится в результате? Посмотрите на примеры на рис. 17.22. Сразу ясно, что этот процесс должен закончиться на исходной вершине тогда и только тогда, когда она имеет нечетную степень в начале процесса.
Один из возможных вариантов состоит в том, что мы прошли весь цикл -тогда доказательство завершено. Иначе все вершины оставшегося графа имеют четные степени, но он может оказаться несвязным. Однако в соответствии с индуктивным предположением каждый его связный компонент содержит эйлеров цикл. Более того, только что удаленный циклический путь связывает эти циклы в эйлеров цикл исходного графа, и остается пройти по этому циклическому пути, отклоняясь на обходы эйлеровых циклов для каждого связного компонента. Каждое такое отклонение представляет собой эйлеров цикл, заканчивающийся в вершине, с которой он начинался. Учтите, что каждое такое отклонение может многократно касаться циклического пути (см. упражнение 17.98). В таком случае обход отклонения выполняется только один раз (например, когда мы впервые с ним сталкиваемся). 
Следствие. Граф содержит эйлеров путь тогда и только тогда, когда он связный и в точности две его вершины имеют нечетную степень.
Доказательство. Эта формулировка эквивалентна формулировке леммы 17.4 для графа, построенного добавлением ребра между двумя вершинами нечетной степени (на концах пути). 
Эти примеры демонстрируют, что путь вдоль ребер, начинающийся в любой вершине графа, в котором имеется эйлеров цикл, всегда возвращается в ту же вершину. Цикл не обязательно проходит через все ребра в графе.
Отсюда следует, например, что никто не может пройти через все мосты Кенигсберга так, чтобы не пройти по одному мосту дважды, поскольку все четыре вершины в соответствующем графе имеют нечетные степени (см. рис. 17.21).
Как было установлено в разделе 17.5, все степени вершин можно найти за время, пропорциональное E для представления списками смежности или множеством ребер, либо за время, пропорциональное V2 для представления графа матрицей смежности -или же в составе представления графа можно использовать вектор, индексированный именами вершин, который содержит степени вершин (см. упражнение 17.42). При наличии такого вектора можно проверить, выполняется ли лемма 17.4, за время, пропорциональное V. Программа 17.18 реализует эту стратегию и показывает, что проверка, имеется ли в заданном графе эйлеров цикл, представляет собой достаточно простую вычислительную задачу. Это важно, потому что интуитивно совсем непонятно, проще ли эта задача, чем определение, существует ли гамильтонов путь в заданном графе.
Программа 17.18. Существование эйлерова цикла
Этот класс позволяет клиентским программам проверить существование эйлерова цикла в графе. Вершины v и w рассматриваются как приватные члены данных, чтобы клиенты могли вывести путь с помощью функции-члена show (которая использует приватную функцию-член tour) (см. программу 17.19).
Для выполнения проверки используются следствие из леммы 17.4 и программа 17.11. Она выполняется за время, пропорциональное V, не считая времени на предварительную обработку, когда выполняется проверка связности и построение таблицы степеней вершин типа DEGREE.
template <class Graph>
class ePATH {
Graph G;
int v, w;
bool found;
STACK <int> S;
int tour(int v);
public:
ePATH(const Graph &G, int v, int w) :
G(G), v(v), w(w)
{ DEGREE<Graph> deg(G);
int t = deg[v] + deg[w];
if ((t % 2) != 0) { found = false; return; }
for (t = 0; t < G.V(); t++)
if ((t != v) && (t != w))
if ((deg[t] % 2) != 0)
{ found = false; return; }
found = true;
}
bool exists() const
{ return found; }
void show();
} ;
А теперь предположим, что требуется найти сам эйлеров цикл. Прямая рекурсивная реализация (поиск пути с помощью проверки ребра с последующим рекурсивным вызовом для поиска пути в остальной части графа) обеспечивает ту же факториальную производительность, что и программа 17.17. Но с такой производительностью мириться не хочется, ведь проверить существование такого пути довольно легко, и мы попробуем отыскать более приемлемый алгоритм. Можно избежать факториальной зависимости с помощью проверки за фиксированное время, можно ли использовать конкретное ребро (в отличие от неизвестных затрат при рекурсивных вызовах), но мы оставим этот подход на самостоятельную проработку (см. упражнения 17.96 и 17.97).
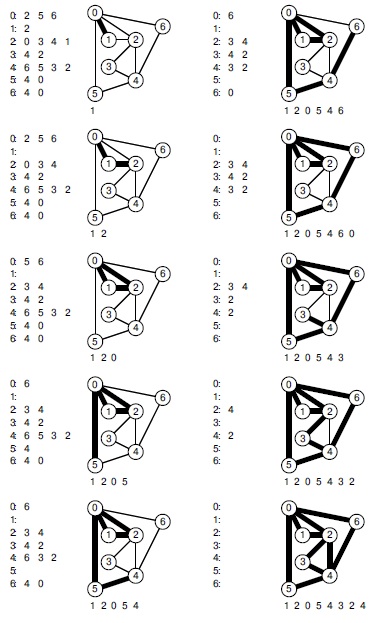
Другой подход вытекает из доказательства леммы 17.4. Можно пройти по циклическому пути, удаляя все использованные ребра и помещая в стек все встреченные вершины, чтобы можно было (1) проследить свой путь с текущей точки до начала и вывести его ребра, и (2) проверить каждую вершину на наличие боковых путей (которые можно включить в главный путь). Этот процесс показан на рис. 17.23.
Программа 17.19 представляет собой реализацию этого подхода. В ней предполагается, что эйлеров цикл существует, и в ней уничтожается локальная копия графа; поэтому важно, чтобы в классе Graph, который использует рассматриваемая программа, имелся конструктор копирования, который создает полностью автономную копию графа. Программный код достаточно сложен, поэтому новичкам можно отложить его разбор до знакомства с алгоритмами обработки графов, рассмотренными в нескольких последующих лекциях. Мы включили ее в этот раздел, чтобы показать, что хорошие алгоритмы и умелая их реализация позволяют исключительно эффективно решать некоторые задачи обработки графов.
Здесь на простом графе показано, как программа 17.19 находит эйлеров цикл с началом и концом в вершине 0. Жирные ребра -те, которые входят в цикл, содержимое стека показано под каждой диаграммой, а списки смежности для ребер, не попавших в цикл, показаны слева от диаграмм.
Сначала программа добавляет в искомый цикл ребро 0-1 и удаляет его из списков смежности (из двух мест) (верхняя левая диаграмма, списки слева). Затем она точно так же добавляет в цикл ребро 1-2 (вторая сверху левая диаграмма). Потом она поворачивает назад в 0, но продолжает строить цикл 0-5-4-6-0 и возвращается в вершину 0, у которой больше не осталось инцидентных ребер (вторая сверху правая диаграмма). Затем она выталкивает из стека изолированные вершины 0 и 6, так что вверху стека остается вершина 4, и начинает цикл с 4 (третья сверху правая диаграмма), проходит через вершины 3, 2 и возвращается в 4, после чего из стека выталкиваются все уже изолированные вершины 4 , 2 , 3 и т.д. Последовательность вытолкнутых из стека вершин определяет эйлеров цикл 0-6-4-2-3-4-5-0-2-1-0 для всего графа.
Лемма 17.5. Если в графе существует эйлеров цикл, то его можно найти за линейное время.
Полное доказательство этой леммы методом индукции мы оставляем на самостоятельную проработку (см. упражнение 17.100). По существу, после первого вызова функции path в стеке содержится путь от v до w, а оставшаяся часть графа (после удаления изолированных вершин) состоит из связных компонентов меньших размеров (имеющих по крайней мере одну общую вершину с найденным на текущий момент путем), которые также содержат эйлеровы циклы. Изолированные вершины выталкиваются из стека, и с помощью функции path продолжается аналогичный поиск эйлеровых циклов, которые содержат неизолированные вершины. Каждое ребро графа заталкивается в стек (и выталкивается из него) в точности один раз, поэтому общее время выполнения пропорционально E. 
Программа 17.19. Поиск эйлерова пути с линейным временем выполнения
Данная реализация функции show для класса из программы 17.18 выводит эйлеров путь между двумя заданными вершинами, если он существует. В отличие от многих других наших реализаций, этот код основан на реализации АТД Graph с конструктором копирования, поскольку он создает копию графа, а потом уничтожает эту копию, удаляя ребра из графа при выводе пути. При наличии линейной по времени реализации функции remove (см. упражнение 17.46) функция show выполняется за линейное время. Приватная функция-член tour проходит по ребрам циклического пути, удаляет их и помещает вершины в стек, чтобы выявить наличие боковых циклов (см. текст). Главный цикл вызывает функцию tour до тех пор, пока существуют боковые циклы.
template <class Graph>
int ePATH<Graph>::tour(int v)
{ while (true)
{ typename Graph::adjIterator A(G, v);
int w = A.beg();
if (A.end()) break;
S.push(v);
G.remove(Edge(v, w));
v = w;
}
return v;
}
template <class Graph>
void ePATH<Graph>::show()
{ if (found) return;
while (tour(v) == v && !S.empty())
{ v = S.pop(); cout << "-" << v; }
cout << endl;
}
Хотя эйлеровы циклы позволяют систематически обойти все ребра и вершины, они довольно редко используются на практике, т.к. лишь немногие графы содержат такие циклы. Вместо этого для исследования графов обычно применяется поиск в глубину, который подробно рассматривается в "Поиск на графе" . Вообще-то, как мы убедимся позже, поиск в глубину на неориентированном графе эквивалентен вычислению двунаправленного эйлерова цикла (two-way Euler tour) -пути, который проходит по каждому ребру в точности дважды, по одному разу в каждом направлении.
Итак, в данном разделе мы увидели, что нетрудно найти простые пути в графе, еще легче определить, можно ли обойти все ребра большого графа, не проходя ни по одному из них дважды (достаточно лишь проверить, что все вершины имеют четные степени), и что даже существует хитрый алгоритм, способный найти такой цикл -однако практически невозможно узнать, можно ли обойти все вершины графа, не посетив ни одну из них дважды. Имеются рекурсивные решения всех этих задач, однако экспоненциальное время выполнения делает эти решения практически бесполезными. Другие решения позволяют получить быстродействующие алгоритмы, удобные для практического применения.
Такой разброс трудности решения с виду похожих задач характерен для обработки графов и является фундаментальным фактом в теории вычислений. На основе краткого анализа в разделе 17.8 и более подробного в части 8 приходится признать, что существует непреодолимый барьер между задачами с экспоненциальным временем решения (такими как задача поиска гамильтонова цикла и многие другие реальные задачи), и задачами, о которых нам известно, что алгоритмы их решения гарантированно выполняются за полиномиальное время (такими как задача поиска эйлерова цикла и многие другие практические задачи). В данной книге основной нашей целью является разработка эффективных алгоритмов решения задач второго из этих классов.
Упражнения
17.85. Покажите в стиле упражнения 17.17 трассу рекурсивных вызовов (и пропущенные вершины) при поиске программой 17.16 пути из вершины 0 в вершину 5 в графе 3-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4.
17.86. Добавьте в рекурсивную функцию из программы 17.16 возможность вывода трассы, как на рис. 17.17, используя для этого глобальную переменную, как описано в тексте.
17.87. Выполните упражнение 17.86, добавив в рекурсивную функцию аргумент, позволяющий отслеживать глубину рекурсии.
17.88. Используя метод, описанный в тексте, напишите реализацию класса sPATH с общедоступной функцией-членом, которая вызывает клиентскую функцию для каждого ребра на пути из v в w, если такой путь существует.
17.89. Измените программу 17.16 так, чтобы она принимала третий аргумент d и проверяла существование пути, соединяющего вершины u и v, длина которого больше d. А именно, значение search(v, v, 2) должно быть ненулевым тогда и только тогда, когда v содержится в некотором цикле.
17.90. Эмпирически определите вероятность того, что программа 17.16 найдет путь между двумя наугад выбранными вершинами в различных графах (см. упражнения 17.63—17.76) и вычислите среднюю длину пути, найденного для различных видов графов.
17.91. Рассмотрим графы, заданные следующими четырьмя наборами ребер:
0-10-20-31-31-42-52-93-64-74-85-85-96-76-97-8
0-10-20-31-30-32-55-63-64-74-85-85-96-76-98-8
0-11-21-30-30-42-52-93-64-74-85-85-96-76-97-8
4-17-96-27-35-00-20-81-63-96-32-81-59-84-54-7
Какие из этих графов содержат эйлеровы циклы? Какие из них содержат гамильтоновы циклы?
17.92. Сформулируйте необходимые и достаточные условия существования в ориентированном графе (ориентированного) эйлерова цикла.
17.93. Докажите, что каждый связный неориентированный граф содержит двунаправленный эйлеров цикл.
17.94. Измените доказательство леммы 17.4, чтобы оно годилось и для графов с параллельными ребрами и петлями.
17.95. Покажите, что если добавить еще один мост, то задача о Кенигсбергских мостах будет иметь решение.
17.96. Докажите, что в связном графе имеется эйлеров путь из v в w только в том случае, если он содержит ребро, инцидентное v, удаление которого не нарушает связности графа (если не учитывать возможной изоляции вершины v).
17.97. Воспользуйтесь упражнением 17.96 для разработки эффективного рекурсивного метода поиска эйлерова цикла в графе, если такой цикл существует. Помимо функций базового АТД графа, можно воспользоваться классами, рассматриваемыми в данной главе, которые определяют степени вершин (см. программу 17.11) и проверяют, существует ли путь между двумя заданными вершинами (см. программу 17.16). Реализуйте и протестируйте полученную программу как на разреженных, так и на насыщенных графах.
17.98. Приведите пример, когда граф, оставшийся после первого вызова функции path из программы 17.19, будет несвязным (в графе, содержащем эйлеров цикл).
17.99. Опишите, как надо изменить программу 17.19, чтобы ее можно было использовать для определения существования эйлерова цикла в заданном графе за линейное время.
17.100. Приведите полное доказательства методом индукции, что алгоритм поиска эйлерова пути, выполняемый за линейное время, который описан в тексте и реализован в программе 17.19, правильно находит эйлеров цикл.
17.101. Найдите количество содержащих эйлеров цикл графов с V вершинами для максимального числа V, для которого вы можете выполнять реальные вычисления.
17.102. Эмпирически определите для различных графов среднюю длину пути, найденного первым вызовом функции path в программе 17.19 (см. упражнения 17.63—17.76). Вычислите вероятность того, что этот путь является циклом.
17.103. Напишите программу, которая вычисляет последовательность из 2n + n -1 битов, в которой никакие две последовательности из n следующих подряд битов не совпадают. (Например, для n = 3 таким свойством обладает последовательность 0001110100.) Примечание: Найдите эйлеров цикл в орграфе де Брюйна.
17.104. Покажите в стиле рис. 17.19 трассу рекурсивных вызовов (и пропущенные вершины) при поиске программой 17.16 гамильтонова цикла в графе
3-71-47-80-55-23-82-90-64-92-66-4.
17.105. Добавьте в программу 17.17 возможность вывода гамильтонова цикла, если он будет найден.
17.106. Найдите гамильтонов цикл в графе
1-22-54-22-60-83-01-33-61-01-44-04-66-52-6
6-99-03-14-39-24-96-97-95-09-77-34-50-57-8,
либо докажите, что он не существует.
17.107. Найдите количество содержащих гамильтонов цикл графов с V вершинами для максимального значения V, для которого вы можете выполнять реальные вычисления.