|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Хеширование
Двойное хеширование
Основной принцип линейного опробования (а, вообще-то, и любого метода хеширования) —гарантирование того, что при поиске конкретного ключа мы просматриваем каждый ключ, который отображается в тот же адрес в таблице (в частности, сам ключ, если он есть в таблице). Однако при использовании схемы с открытой адресацией, как правило, просматриваются и другие ключи, особенно когда заполнение таблицы велико. В примере, приведенном на рис. 14.7, при поиске ключа N просматриваются ключи C, E, R и I, ни один из которых не имеет такого же хеш-значения. Что еще хуже, вставка ключа с одним хеш-значением может существенно увеличить время поиска ключей с другими хеш-значениями: на рис. 14.7 вставка ключа M приводит к увеличению времени поиска для позиций 7-12 и 0-1. Это явление называется кластеризацией (clustering), поскольку оно связано с процессом образования кластеров. Для почти заполненных таблиц оно может значительно замедлять линейное опробование.
К счастью, существует простой способ избежать возникновения проблемы кластеризации — двойное хеширование (double hashing). Основная стратегия остается той же, что и при выполнении линейного опробования; единственное различие состоит в том, что вместо просмотра каждой позиции таблицы, следующей за коллизией, мы используем вторую хеш-функцию для получения постоянного шага, используемого для последовательных проб. Реализация этого способа приведена в программе 14.6.
Программа 14.6. Двойное хеширование
Двойное хеширование аналогично линейному опробованию, за исключением того, что здесь используется вторая хеш-функция — для определения шага поиска, используемого после каждой коллизии. Шаг поиска должен быть ненулевым, а размер таблицы и шаг поиска должны быть взаимно простыми числами. Функция remove для линейного опробования (см. программу 14.5) не работает с двойным хешированием, поскольку любой ключ может присутствовать во многих различных последовательностях проб.
void insert(Item item)
{ Key v = item.key();
int i = hash(v, M), k = hashtwo(v, M);
while (!st[i].null()) i = (i+k) % M;
st[i] = item; N+ + ;
}
Item search(Key v)
{ int i = hash(v, M), k = hashtwo(v, M);
while (!st[i].null())
if (v == st[i].key())
return st[i];
else
i = ( i+k) % M;
return nullItem;
}
Выбор второй хеш-функции требует определенной осторожности, поскольку в противном случае программа может вообще не работать. Во-первых, необходимо исключить случай, когда вторая хеш-функция дает нулевое значение, поскольку при первой же коллизии это приведет к бесконечному циклу. Во-вторых, важно, чтобы значение второй хеш-функции и размер таблицы были взаимно простыми числами, т.к. иначе некоторые из последовательностей проб могут оказаться очень короткими (например, в случае, когда размер таблицы вдвое больше значения второй хеш-функции). Один из способов претворения этих правил в жизнь — выбор в качестве M простого числа и выбор второй хеш-функции, возвращающей значения, меньшие M. На практике во многих ситуациях, если размер таблицы не слишком мал, будет достаточно простой второй хеш-функции вроде
inline int hashtwo(Key v) { return (v % 97) + 1; }
Кроме того, любое снижение эффективности (из-за уменьшения дисперсии), вызываемое данным упрощением, на практике, скорее всего, будет не только не важно, но и вовсе незаметно. Если таблица большая и разреженная, сам размер таблицы не обязательно должен быть простым числом, поскольку для каждого поиска нужно будет лишь несколько проб (хотя было бы неплохо для предотвращения бесконечного цикла выполнять проверки на длинные последовательности проб и прерывать их — см. упражнение 14.38).
На рис. 14.9 показан процесс построения небольшой таблицы методом двойного хеширования, а из рис. 14.10 видно, что двойное хеширование приводит к образованию значительно меньшего количества кластеров (которые поэтому значительно короче), чем в результате линейного опробования.
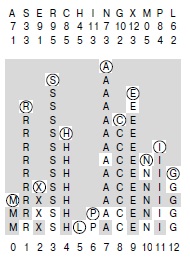
На этой диаграмме показан процесс вставки ключей A S E R C H I N G X M P L в первоначально пустую хеш-таблицу с открытой адресацией с использованием хеш-значений, приведенных вверху, и разрешением коллизий с помощью двойного хеширования. Первое и второе хеш-значения каждого ключа приведены в двух строках под этим ключом. Как и на рис. 14.7, проверяемые позиции таблицы выделены белым цветом. Ключ A попадает в позицию 7, затем S попадает в позицию 3, E — в позицию 9, как и на рис. 14.7. Но ключ R после коллизии в позиции 9 попадает в позицию 1; его второе хеш-значение, равное 5, используется в качестве шага последовательности проб после коллизии. Аналогично, ключ P окончательно попадает в позицию 6 после коллизий в позициях 8, 12, 3, 7, 11 и 2 при использовании в качестве шага его второго хеш-значения, равного 4.
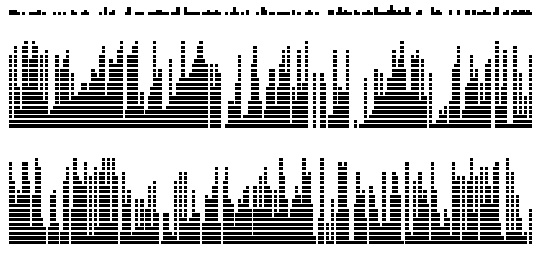
На этих диаграммах показано размещение записей при их вставке в хеш-таблицу с использованием линейного опробования (в центре) и двойного хеширования (внизу), при распределении ключей, показанном на верхней диаграмме. Каждая черточка показывает результат вставки 10 записей. По мере заполнения таблицы записи объединяются в кластеры, разделенные пустыми позициями таблицы. Длинные кластеры нежелательны, т.к. средние затраты на поиск одного ключа в кластере пропорциональны длине кластера. В случае линейного опробования чем длиннее кластеры, тем более вероятно их удлинение, поэтому по мере заполнения таблицы оказываются доминирующими несколько длинных кластеров. При использовании двойного хеширования этот эффект значительно менее выражен, и кластеры остаются сравнительно короткими.
Лемма 14.4. При разрешении коллизий с помощью двойного хеширования среднее количество проб, необходимых для выполнения поиска в хеш-таблице размером M, содержащей 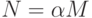 ключей, равно
ключей, равно 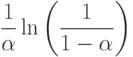 и
и 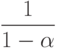
соответственно для успешного и неудачного поиска.
Эти формулы — результат глубокого математического анализа, выполненного Гиба (Guibas) и Шемереди (Szemeredi) (см. раздел ссылок). Доказательство основывается на том, что двойное хеширование почти эквивалентно более сложному алгоритму случайного хеширования, при котором используется зависящая от ключей последовательность позиций опробования, обеспечивающая равную вероятность попадания каждой пробы в каждую позицию таблицы. Этот алгоритм всего лишь аппроксимирует двойное хеширование, по многим причинам: например, очень трудно гарантировать, что при двойном хешировании каждая позиция таблицы проверяется хотя бы один раз, но при случайном хешировании одна и та же позиция таблицы может проверяться и более одного раза.
Однако для разреженных таблиц вероятность возникновения коллизий при использовании обоих методов одинакова. Интерес представляют оба метода: двойное хеширование легко реализовать, а случайное хеширование легко анализировать.
При случайном хешировании средние затраты на неудачный поиск определяются равенством
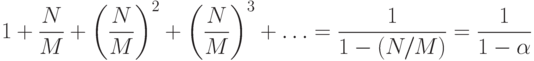
Выражение слева — сумма вероятностей, что при неудачном поиске используются более к проб, при к = 0, 1, 2, ... (на основании элементарной теории вероятностей она равна средней вероятности). При поиске всегда используется одна проба, затем с вероятностью N/M требуется вторая проба, с вероятностью (N/M)2 — третья проба и т.д. Эту же формулу можно использовать для вычисления следующего приближенного значения средней стоимости успешного поиска в таблице, содержащей N ключей:
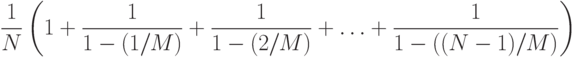
Вероятность успешного поиска одинакова для всех ключей в таблице; затраты на отыскание ключа равны затратам на его вставку, а затраты на вставку j-го ключа в таблицу равны затратам на неудачный поиск в таблице, содержащей j — 1 ключ, поэтому данная формула определяет среднее значение этих затрат.
Теперь эту сумму можно упростить и вычислить, умножив числители и знаменатели всех дробей на M:

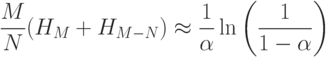
 .
. 
Точная природа взаимосвязи между производительностью двойного хеширования и идеальным случаем случайного хеширования, установленной Гиба и Шемереди — асимптотическое приближение, которое не обязательно должно быть справедливо для используемых на практике размеров таблиц. Кроме того, полученные результаты основываются на предположении, что хеш-функции возвращают случайные значения. Но все же асимптотические формулы из свойства 14.5 на практике позволяют достаточно точно предсказать производительность двойного хеширования, даже при использовании такой просто вычисляемой второй хеш-функции, как (v % 97)+1. Как и соответствующие формулы для линейного опробования, при приближении значения а к 1 эти формулы стремятся к бесконечности, но гораздо медленнее.
Различие между линейным опробованием и двойным хешированием хорошо видно на рис. 14.11. В разреженных таблицах двойное хеширование и линейное опробование имеют схожую производительность, но при использовании двойного хеширования можно допустить значительно большую степень заполнения таблицы, чем при использовании линейного опробования, прежде чем производительность заметно снизится. В следующей таблице приведено ожидаемое количество проб для успешного и неудачного поиска при использовании двойного хеширования:
коэффициент загрузки ( ) )
|
1/2 | 2/3 | 3/4 | 9/10 |
|---|---|---|---|---|
| успешный поиск | 1,4 | 1,6 | 1,8 | 2,6 |
| неудачный поиск | 1,5 | 2,0 | 3,0 | 5,5 |
Неудачный поиск всегда требует больших затрат, чем успешный, но и тому, и другому в среднем требуется лишь несколько проб, даже в таблице, заполненной на девять десятых.
Можно взглянуть на эти результаты и под другим углом: для получения такого же среднего времени поиска двойное хеширование позволяет использовать меньшие таблицы, чем нужно при использовании линейного опробования.
На этих графиках показаны затраты на построение хеш-таблицы размером 1000 вставками ключей в первоначально пустую таблицу с помощью линейного опробования (вверху) и двойного хеширования (внизу). Каждый вертикальный столбец представляет затраты на вставку 20 ключей. Серые кривые — теоретически предсказанные затраты (см. леммы 14.4 и 14.5).
Лемма 14.5. Сохраняя коэффициент загрузки меньшим, чем 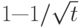 для линейного опробования и меньшим, чем
для линейного опробования и меньшим, чем 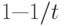 для двойного хеширования, можно обеспечить, что в среднем для выполнения всех поисков потребуется меньше t проб.
для двойного хеширования, можно обеспечить, что в среднем для выполнения всех поисков потребуется меньше t проб.
Установите значения выражений для неудачного поиска в свойствах 14.4 и 14.5 равными t и решите уравнения относительно  .
. 
Например, чтобы среднее количество проб при поиске было меньшим 10, при использовании линейного опробования необходимо сохранять таблицу пустой не менее чем на 32%, а при использовании двойного хеширования — лишь на 10%. Чтобы можно было выполнить неудачный поиск менее чем за 10 проб при обработке 105 элементов, нужно свободное место лишь для 104 дополнительных элементов. В то же время при использовании цепочек переполнения потребовалась бы дополнительная память для более чем 105 ссылок, а при использовании деревьев бинарного поиска — еще вдвое больший объем памяти.
Метод реализации операции удалить, приведенный в программе 14.5 (повторное хеширование ключей, для которых путь поиска может содержать удаляемый элемент), для двойного хеширования не годится, т.к. удаленный элемент может присутствовать во многих различных последовательностях проб для ключей, разбросанных по всей таблице. Поэтому приходится применять другой метод, рассмотренный в конце "Таблицы символов и деревья бинарного поиска" : удаленный элемент заменяется сигнальным элементом, помечающим позицию таблицы как занятую, но не соответствующим ни одному из ключей (см. упражнение 14.33).
Подобно линейному опробованию, двойное хеширование не годится в качестве основы для реализации полнофункционального АТД таблицы символов, в котором необходимо поддерживать операции сортировать или выбрать.
Упражнения
14.31. Приведите содержимое хеш-таблицы, образованной вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустую таблицу размером М = 16 при использовании двойного хеширования. Воспользуйтесь хеш-функцией 11k mod М для первой пробы и второй хеш-функцией (k mod 3) + 1 для шага поиска (если ключ является k-ой буквой алфавита).
14.32. Выполните упражнение 14.31 для М = 10.
14.33. Реализуйте удаление для двойного хеширования с использованием сигнального элемента.
14.34. Измените решение упражнения 14.27, чтобы в нем использовалось двойное хеширование.
14.35. Измените решение упражнения 14.28, чтобы в нем использовалось двойное хеширование.
14.36. Измените решение упражнения 14.29, чтобы в нем использовалось двойное хеширование.
14.37. Реализуйте алгоритм, который аппроксимирует случайное хеширование, используя ключ в качестве исходного значения для встроенного в программу генератора случайных чисел (как в программе 14.2).
14.38. Пусть таблица, размер которой равен 106, заполнена наполовину, причем занятые позиции распределены случайным образом. Оцените вероятность того, что заняты все позиции, индексы которых кратны 100.
14.39. Допустим, что в коде реализации двойного хеширования присутствует ошибка, приводящая к тому, что одна или обе хеш-функции всегда возвращают одно и то же (ненулевое) значение. Опишите, что происходит в каждой из следующих ситуаций: (1) когда ошибочна первая функция, (2) когда ошибочна вторая функция, (3) когда ошибочны обе функции.