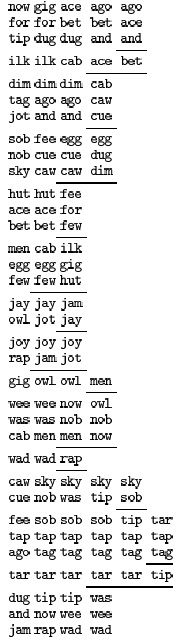Поразрядная сортировка

Трехпутевая поразрядная быстрая сортировка

Еще одна возможность приспособить быструю сортировку для выполнения MSD-сортировки заключается в использовании трехпутевого разбиения по старшим байтам ключей, переходя к следующему байту только в среднем подфайле (с ключами, старшие байты которых равны старшему байту центрального элемента). Этот метод можно легко реализовать (достаточно одного оператора описания плюс кода трехпутевого разбиения из программы 7.5) и адаптировать к различным ситуациям. Полная реализация этого метода приведена в программе 10.3.

По существу, выполнение трехпутевой поразрядной быстрой сортировки равносильно сортировке файла по старшим символам ключей (с помощью быстрой сортировки) с последующим рекурсивным применением этого метода к оставшимся ключам. При сортировке строк этот метод показывает лучшие результаты в сравнении с обычной быстрой сортировкой и MSD-сортировкой. Вообще-то его можно рассматривать как гибрид этих двух алгоритмов.

Сравнивая трехпутевую поразрядную быструю сортировку со стандартной MSD-сортировкой, можно заметить, что она разбивает файл всего лишь на три части, и поэтому не использует преимуществ быстрого многопутевого разбиения, особенно на ранних стадиях сортировки. С другой стороны, на поздних стадиях MSD-сортировки появляется множество пустых контейнеров, в то время как трехпутевая поразрядная быстрая сортировка хорошо работает для повторяющихся ключей, ключей из узкого диапазона, небольших файлов и других случаев, которые тормозят выполнение MSD-сортировки.

Программа 10.3. Трехпутевая поразрядная быстрая сортировка

Данная MSD-сортировка по существу эквивалентна коду быстрой сортировки с трехпутевым разбиением (программа 7.5), но отличается от нее следующим: (1) обращения к ключам заменены обращениями к байтам ключей, (2) текущая позиция байта передается рекурсивной программе в виде параметра, и (3) рекурсивные вызовы для среднего подфайла переходят к следующему байту. Чтобы индексы не выходили за пределы строк, перед рекурсивными вызовами с переходом к следующему байту выполняется проверка, равно ли 0 центральное значение. Если центральное значение равно 0, то левый подфайл пуст, средний под-файл соответствует найденным равным ключам, а правый подфайл соответствует более длинным строкам, которые требуют дальнейшей обработки.

  #define ch(A) digit(A, d)
  template <class Item>
  void quicksortX(Item a[], int l, int r, int d)
    { int i, j, k, p, q; int v;
      if (r-l <= M) { insertion(a, l, r); return; }
      v = ch(a[r]); i = l-1; j = r; p = l-1; q = r;
      while ( i < j )
        { while (ch(a[ + + i]) < v) ;
          while (v < ch(a[-- j ] ) ) if (j == l) break;
          if (i > j) break;
          exch(a[i], a[j]);
          if (ch(a[i]) == v) { p++; exch(a[p], a[i]); }
          if (v == ch(a[j])) { q—; exch(a[j], a[q]); }
        }
      if (p == q)
       { if (v != '\0') quicksortX(a, l, r, d+1); return; }
      if (ch(a[i]) < v) i++;
      for (k = l; k <= p; k+ + , j--) exch(a[k], a[j]);
      for (k = r; k >= q; k--, i++) exch(a[k], a[i]);
      quicksortX(a, l, j, d);
      if ((i == r) && (ch(a[i]) == v)) i+ + ;
      if (v != '\0') quicksortX(a, j + 1, i-1, d+1);
      quicksortX(a, i, r, d);
    }
      

Рис. 10.11. Трехпутевая поразрядная быстрая сортировка

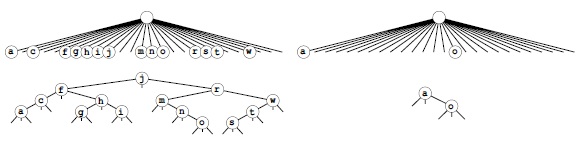
Файл делится на три части: слова, начинающиеся с букв от a до i, слова, начинающиеся c буквы j, и слова, начинающиеся с букв от к до z. Затем сортировка рекурсивно продолжается.

Особенно важно то, что разбиение адаптируется к различным закономерностям в разных частях ключа. Более того, для него не нужен вспомогательный массив. Эти достоинства уравновешиваются тем, что если подфайлов много, то для реализации многопутевого разбиения с помощью последовательности трехпутевых разбиений требуются дополнительные обмены.

На рис. 10.11 приведен пример действия этого метода при сортировке трехбуквенных слов, представленных на рис. 10.7, а на рис. 10.12 показана структура рекурсивных вызовов. Каждый узел соответствует в точности трем рекурсивным вызовам: для ключей с меньшим значением первого байта (левый потомок), для ключей с тем же значением первого байта (средний потомок) и для ключей с большим значением первого байта (правый потомок).

Если сортируемые ключи соответствуют абстракции из раздела 10.2, стандартную быструю сортировку и все другие методы сортировки, рассмотренные в главах 6—9, можно рассматривать как MSD-сортировку, поскольку функция сравнения осуществляет доступ сначала к наиболее значащей части ключа (см. упражнение 10.3).

Рис. 10.12. Рекурсивная структура трехпутевой поразрядной быстрой сортировки

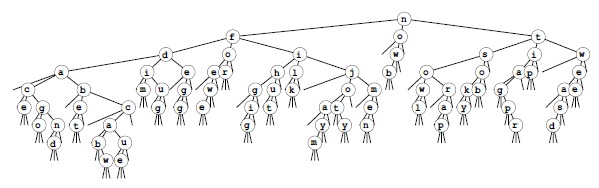
Данная комбинация обычного и trie-дерева соответствует замене 26-путевыхузлов в trie-дереве, изображенном на рис. 10.10, на тернарные деревья бинарного поиска, как показано на рис. 10.13. Любой путь от корня вниз, который оканчивается средней связью, определяет ключ файла — с помощью символов, указанных средними ссылками на этом пути. На рис. 10.10 имеется 1035 не показанных пустых ссылок, на данном рисунке показаны все 155 пустых ссылок этого дерева. Каждая пустая ссылка соответствует пустому контейнеру, так что это различие показывает, как существенно трехпутевоеразбиение может сократить число пустых контейнеров, которые появляются при MSD-сортировке.

Рис. 10.13. Пример узлов trie-дерева трехпутевой поразрядной быстрой сортировки

Трехпутевая поразрядная быстрая сортировка решает проблему пустых корзин, характерную для MSD-сортировки, с помощью выполнения трехпутевого разбиения: значение одного байта устраняется, а остальные обрабатываются дальше. Это действие соответствует замене каждого M-путевого узла trie—дерева, описывающего рекурсивную структуру вызовов MSD-сортировки (см. рис.10.9), на троичное дерево, в котором каждому непустому контейнеру соответствует внутренний узел. Для полных узлов (слева) такое изменение требует затрат времени и почти не экономит память, но для пустых узлов (справа) затраты времени минимальны, а экономия памяти значительна.

Например, при обработке строковых ключей функция сравнения обращается только к старшим байтам, если они различны, к двум байтам, если первые байты совпадают, а вторые байты различны, и т.д. Таким образом стандартный алгоритм автоматически получает часть производительности, присущей MSD-сортировке (см. раздел 7.7 "Быстрая сортировка" ). Существенное различие заключается в том, что стандартный алгоритм не может выполнить никаких специальных действий, если старшие байты равны. Действительно, программу 10.3 можно рассматривать как наделение быстрой сортировки возможностью хранить информацию о старших цифрах элементов после их использования для многократных разбиений. В небольших файлах, где большая часть сравнений уже выполнена, обычно совпадают много старших байтов. Стандартный алгоритм должен просмотреть все эти байты при каждом сравнении, а трехпутевой алгоритм не делает этого.

Рассмотрим случай, когда ключи имеют большую длину (для простоты — фиксированную), но большинство старших байтов совпадают. В такой ситуации время выполнения обычной быстрой сортировки пропорционально длине слова, помноженной на 2 Nln N, тогда как время выполнения поразрядной версии пропорционально N, умноженному на длину слова (чтобы обнаружить все равные между собой старшие байты) плюс 2 Nln N (для сортировки оставшихся коротких ключей). Иначе говоря, этот метод может работать в ln N раз быстрее, чем обычная быстрая сортировка, если учитывать только затраты на сравнения. На практике в приложениях сортировки подобные характеристики ключей не являются чем-то необычным (см. упражнение 10.25).

Другим интересным свойством трехпутевой поразрядной быстрой сортировки является то, что ее характеристики не зависят напрямую от значения основания системы счисления. Для других методов поразрядной сортировки необходим вспомогательный массив, индексированный по основанию системы счисления, и нужно, чтобы размер этого массива не был намного больше размера самого файла. Для данного метода такой массив не нужен. Если в качестве основания взять очень большое значение (больше длины слова), то рассматриваемый метод превращается в обычную быструю сортировку, а если в качестве основания взять число 2, то в обычную бинарную быструю сортировку. Промежуточные же значения основания системы счисления позволяют эффективно делить ключи на равные части.

Для многих практических приложений можно разработать гибридный метод, обладающий великолепной производительностью: применять стандартную MSD-сортировку для упорядочения крупных файлов, пользуясь при этом преимуществами многопутевого разбиения, и трехпутевую поразрядную сортировку с небольшим значением основания системы счисления для меньших файлов, которая позволяет избежать отрицательных эффектов, связанных с наличием большого числа пустых корзин.

Трехпутевая быстрая сортировка успешно применяется и в тех случаях, когда сортируемыми ключами являются векторы (или в математическом смысле, или в смысле стандартной библиотеки шаблонов C++). Другими словами, если ключи составлены из независимых компонентов (каждый из которых сам является абстрактным ключом), можно упорядочить записи таким образом, что они будут располагаться в порядке возрастания первых компонентов ключей и в порядке возрастания вторых компонентов ключей, если равны их первые компоненты и т.д. Сортировку векторов можно рассматривать как обобщение поразрядной сортировки, в котором R может быть произвольно большим. После соответствующей модификации программа 10.3 будет называться многомерной быстрой сортировкой (multikey quicksort).

Упражнения

10.25. Пусть ключи состоят из d байтов (d > 4), причем последние 4 байта принимают случайные значения, а все остальные равны 0. Оцените количество просмотренных байтов при упорядочении с помощью трехпутевой поразрядной быстрой сортировки (программа 10.3) и стандартной быстрой сортировки (программа 7.1) больших файлов размером N, и вычислите отношение значений времени выполнения сортировок.

10.26. Определите опытным путем размер байта, для которого время выполнения трехпутевой сортировки случайных 64-разрядных ключей минимально, при N = 10³, 10⁴, 10⁵ и 10⁶ .

10.27. Разработайте реализацию трехпутевой поразрядной быстрой сортировки для связных списков.

10.28. Разработайте реализацию многомерной быстрой сортировки для случая, когда ключи представляют собой векторы из t чисел с плавающей точкой. Используйте проверку на равенство чисел с плавающей точкой, описанную в упражнении 4.6.

10.29. Используя генератор ключей из упражнения 10.19, выполните трехпутевую поразрядную быструю сортировку для N = 10³, 10⁴, 10⁵ и 10⁶ . Сравните ее производительность с производительностью MSD-сортировки.

10.30. Используя генератор ключей из упражнения 10.21, выполните трехпутевую поразрядную быструю сортировку для N = 10³, 10⁴, 10⁵ и 10⁶ . Сравните ее производительность с производительностью MSD-сортировки.

10.31. Используя генератор ключей из упражнения 10.23, выполните трехпутевую поразрядную быструю сортировку для N = 10³, 10⁴, 10⁵ и 10⁶ . Сравните ее производительность с производительностью MSD-сортировки.