Рекурсия и деревья

Обход графа

В качестве заключительного примера в этой главе рассмотрим одну из наиболее важных рекурсивных программ: рекурсивный обход графа, или поиск в глубину (depth -first search). Этот метод систематического посещения всех узлов графа представляет собой непосредственное обобщение методов обхода деревьев, рассмотренных в разделе 5.6, и служит основой для многих базовых алгоритмов обработки графов (см. часть 7). Это простой рекурсивный алгоритм. Начиная с любого узла v, мы

• посещаем v;
• (рекурсивно) посещаем каждый (не посещенный) узел, связанный с v.

Если граф является связным, со временем будут посещены все узлы. Программа 5.21 является реализацией этой рекурсивной процедуры.

Программа 5.21. Поиск в глубину

Для посещения в графе всех узлов, связанных с узлом к, мы помечаем его как посещенный, а затем (рекурсивно) посещаем все не посещенные узлы в списке смежности узла к.

void traverse(int k, void visit(int))
  { visit(k); visited[k] = 1;
    for (link t = adj[k]; t != 0; t = t ->next)
      if (!visited[t ->v]) traverse(t ->v, visit);
  }
        

Например, предположим, что используется представление в виде списков связности, приведенное для графа на рис. 3.15. На рис. 5.32 приведена последовательность вызовов, выполненных при поиске в глубину в этом графе, а последовательность прохождения ребер графа показана в левой части рис. 5.33. При прохождении каждого из ребер графа возможны два варианта: если ребро приводит к уже посещенному узлу, мы игнорируем его; если оно приводит к еще не посещенному узлу, мы проходим по нему с помощью рекурсивного вызова. Множество всех пройденных таким образом ребер образует остовное дерево графа.

Рис. 5.32. Вызовы функции поиска в глубину

Эта последовательность вызовов функций реализует поиск в глубину для графа, приведенного на рис. 3.15. Дерево, которое описывает структуру рекурсивных вызовов (вверху), называется деревом поиска в глубину.

Различие между поиском в глубину и общим обходом дерева (см. программу 5.14) состоит в том, что необходимо явно исключить посещение уже посещенных узлов. В дереве такие узлы не встречаются. Действительно, если граф является деревом, рекурсивный поиск в глубину, начинающийся с корня, эквивалентен прямому обходу.

Поскольку время, необходимое для построения представления в виде списков смежности из последовательности ребер (см. программу 3.19), также пропорционально V + E, поиск в глубину обеспечивает решение задачи связности из "Введение" с линейным временем выполнения. Однако для очень больших графов решения вида объединение -поиск могут оказаться предпочтительнее, поскольку для представления всего графа нужен объем памяти, пропорциональный E, а для решений объединение -поиск - пропорциональный только V.

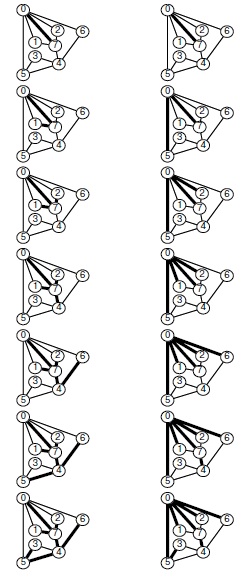
Как и в случае обхода дерева, можно определить метод обхода графа, при котором используется явный стек (см. рис. 5.34). Можно представить себе абстрактный стек, содержащий двойные элементы: узел и указатель на список смежности для этого узла. Если вначале стек содержит начальный узел, а указатель указывает на первый элемент списка смежности для этого узла, алгоритм поиска в глубину эквивалентен входу в цикл, в котором сначала посещается узел из верхушки стека (если он еще не был посещен); потом сохраняется узел, указанный текущим указателем списка смежности; затем ссылка из списка смежности сдвигается на следующий узел (с выталкиванием элемента, если достигнут конец списка смежности); и, наконец, в стек заносится элемент для сохраненного узла со ссылкой на первый узел его списка смежности.

Рис. 5.33. Поиск в глубину и поиск в ширину

При поиске в глубину (слева) перебираются все узлы, с возвратом к предшествующему узлу, когда все связи данного узла проверены. При поиске в ширину (справа) сначала перебираются все связи данного узла, а затем выполняется переход к следующему узлу.

Или же, как это было сделано для обхода дерева, можно создать стек, содержащий только ссылки на узлы. Если вначале стек содержит начальный узел, мы входим в цикл, в котором посещаем узел на верхушке стека (если он еще не был посещен), затем заносим в стек все узлы, смежные с этим узлом. На рис. 5.34 видно, что для нашего примера графа оба метода эквивалентны поиску в глубину, причем эквивалентность сохраняется и в общем случае.

Алгоритм посещения верхнего узла и занесения всех его соседей - простая формулировка поиска в глубину, но из рис. 5.34 понятно, что этот метод может оставлять в стеке нескольких копий каждого узла. Это происходит даже в случае проверки, посещался ли каждый узел, который должен быть помещен в стек, и если да, то отказа от занесения в стек такого узла. Во избежание этой проблемы можно воспользоваться реализацией стека, которая устраняет дублирование с помощью правила "забыть старый элемент ": поскольку ближайшая к верхушке стека копия всегда посещается первой, все остальные копии просто выталкиваются из стека.

Динамика состояния стека для поиска в глубину, показанная на рис. 5.34, основана на том, что узлы каждого списка смежности появляются в стеке в том же порядке, что и в списке. Для получения этого порядка для данного списка смежности при занесении узлов по одному необходимо втолкнуть в стек сначала последний узел, затем предпоследний и т.д.

Рис. 5.34. Динамика стека при поиске в глубину

Стек, обеспечивающий поиск в глубину, можно представить себе как содержащий элементы, каждый из которых состоит из узла и ссылки на список смежности для этого узла (показан узлом в кружке) (слева). Таким образом, обработка начинается с находящегося в стеке узла 0 со ссылкой на первый узел в его списке смежности - узел 7. Каждая строка отражает результат выталкивания из стека, занесения ссылки на следующий узел в списке посещенных узлов и занесения в стек элемента для не посещенных узлов. Этот процесс можно также представить себе в виде простого занесения в стек всех узлов, смежных с любым не посещенным узлом (справа).

Более того, чтобы ограничить размер стека числом вершин и все -таки посещать узлы в том же порядке, как и при поиске в глубину, необходимо использовать стек с забыванием старого элемента. Если посещение узлов в том же порядке, что и при поиске в глубину, не имеет значения, обоих этих осложнений можно избежать и непосредственно сформулировать нерекурсивный метод обхода графа с использованием стека, который выглядит так. После первоначального занесения в стек начального узла мы входим в цикл, в котором посещаем узел на верхушке стека, затем обрабатываем его список смежности, помещая в стек каждый узел (если он еще не был посещен); здесь должна использоваться реализация стека, которая запрещает дублирование по правилу "игнорировать новый элемент ". Этот алгоритм обеспечивает посещение всех узлов графа аналогично поиску в глубину, но не является рекурсивным.

Алгоритм, описанный в предыдущем абзаце, заслуживает внимания, поскольку вместо стека можно использовать любой АТД обобщенной очереди и все же посетить каждый из узлов графа (плюс сгенерировать развернутое дерево). Например, если вместо стека задействовать очередь, то получится поиск в ширину, который аналогичен обходу дерева по уровням. Программа 5.22 - реализация этого метода (при условии, что используется реализация очереди наподобие программы 4.12); пример этого алгоритма в действии показан на рис. 5.35. В части 6 будет рассмотрено множество алгоритмов обработки графов, основанных на более сложных АТД обобщенных очередей.

И при поиске в ширину, и при поиске в глубину посещаются все узлы графа, но в совершенно различном порядке (см. рис. 5.36). Поиск в ширину подобен армии разведчиков, разосланных по всей территории; поиск в глубину соответствует единственному разведчику, который проникает как можно дальше вглубь неизведанной территории, возвращаясь только в случае, если наталкивается на тупик. Это базовые методы решения задач, играющих существенную роль во многих областях компьютерных наук, а не только в поиске в графах.

Программа 5.22. Поиск в ширину

Чтобы посетить в графе все узлы, связанные с узлом к, узел к помещается в очередь FIFO, затем выполняется цикл, в котором из очереди выбирается следующий узел и, если он еще не был посещен, он посещается, а в стек заталкиваются все не посещенные узлы из его списка смежности. Этот процесс продолжается до тех пор, пока очередь не опустеет.

void traverse(int k, void visit(int))
  {
    QUEUE<int> q(V*V);
    q.put(k);
    while (!q.empty())
      if (visited[k = q.get()] == 0)
        {
          visit(k); visited[k] = 1;
          for (link t = adj[k]; t != 0; t = t ->next)
if (visited[t ->v] == 0) q.put(t ->v);
        }
  }
        

Рис. 5.35. Динамика очереди при поиске в ширину

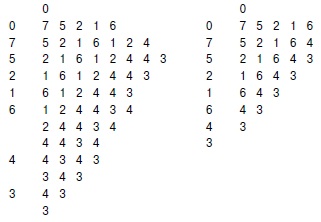
Обработка начинается с узла 0 в очереди, затем мы извлекаем узел 0, посещаем его и помещаем в очередь узлы 7 5 2 1 6 из его списка смежности, причем именно в этом порядке. Затем мы извлекаем узел 7, посещаем его и помещаем в очередь узлы из его списка смежности, и т.д. В случае запрета дублирования по правилу "игнорировать новый элемент " (справа) мы получаем такой же результат без лишних элементов в очереди.

Рис. 5.36. Деревья обхода графов

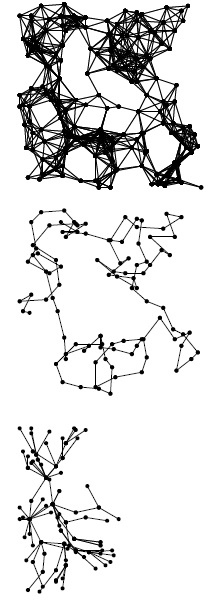
На этой схеме показаны поиск в глубину (в центре) и поиск в ширину (внизу), выполненные наполовину в большом графе (вверху). При поиске в глубину обход выполняется от одного узла к следующему, так что большинство узлов связано только с двумя другими.

А при поиске в ширину посещаются все узлы, связанные с данным, прежде чем двигаться дальше; поэтому некоторые узлы связаны с множеством других.

Упражнения

5.92. Построив диаграммы, соответствующие рис. 5.33 (слева) и 5.34 (справа), покажите, как происходит посещение узлов при рекурсивном поиске в глубину в графе, построенном для последовательности ребер 0 -2, 1 -4, 2 -5, 3 -6, 0 -4, 6 -0 и 1 -3 (см. упражнение 3.70).

5.93. Построив диаграммы, соответствующие рис. 5.33 (слева) и 5.34 (справа), покажите, как происходит посещение узлов при поиске в ширину (с использованием стека) в графе, построенном для последовательности ребер 0 -2, 1 -4, 2 -5, 3 -6, 0 -4, 6 -0 и 1 -3 (см. упражнение 3.70).

5.94. Построив диаграммы, соответствующие рис. 5.33 (слева) и 5.35 (справа), покажите, как происходит посещение узлов при поиске в ширину (с использованием очереди) в графе, построенном для последовательности ребер 0 -2 , 1 -4 , 2 -5, 3 -6, 0 -4, 6 -0 и 1 -3 (см. упражнение 3.70).

5.95. Почему время выполнения, упоминаемое в лемме 5.10, пропорционально V + E, а не просто E ?

5.96. Построив диаграммы, соответствующие рис. 5.33 (слева) и 5.35 (справа), покажите, как происходит посещение узлов при поиске в глубину (с использованием стека и правила "забыть старый элемент ") в графе, приведенном на рис. 3.15.

5.97. Построив диаграммы, соответствующие рис. 5.33 (слева) и 5.35 (справа), покажите, как происходит посещение узлов при поиске в глубину (с использованием стека и правила "игнорировать новый элемент ") в графе, приведенном на рис. 3.15.

5.98. Реализуйте поиск в глубину с использованием стека для графов, которые представлены списками смежности.

5.99. Реализуйте рекурсивный поиск в глубину для графов, которые представлены списками смежности.

Перспективы

Рекурсия лежит в основе ранних теоретических исследований природы вычислений. Рекурсивные функции и программы играют главную роль в математических исследованиях, в которых предпринимается попытка разделения задач на поддающиеся решению на компьютере и на непригодные для этого.

В ходе столь краткого рассмотрения просто невозможно полностью осветить столь обширные темы, как деревья и рекурсия. Многие самые удачные примеры рекурсивных программ будут постоянно встречаться нам на протяжении всей книги - к ним относятся алгоритмы "разделяй и властвуй " и рекурсивные структуры данных, которые успешно применяются для решения широкого спектра задач. Для многих приложений нет смысла выходить за рамки простой непосредственной рекурсивной реализации; для других будет рассмотрен вывод нерекурсивных и восходящих реализаций.

В этой книге основное внимание уделено практическим аспектам построения рекурсивных программ и структур данных. Наша цель - применение рекурсии для создания изящных и эффективных реализаций. Для достижения этой цели необходимо особо учитывать опасности использования простых программ, которые ведут к экспоненциальному увеличению количества вызовов функций или недопустимо большой глубине вложенности. Несмотря на этот недостаток, рекурсивные программы и структуры данных весьма привлекательны, поскольку часто они наводят на индуктивные рассуждения, которые помогают убедиться в правильности и эффективности разработанных программ.

В данной книге деревья используются как для упрощения понимания динамических свойств программ, так и в качестве динамических структур данных. В главах 12 - 15 особенно большое внимание уделяется работе с древовидными структурами. Свойства, описанные в этой главе, предоставляют базовую информацию, которая требуется для эффективного применения древовидных структур.

Несмотря на центральную роль в разработке алгоритмов, рекурсия - вовсе не панацея на все случаи жизни. Как было показано при изучении алгоритмов обхода деревьев и графов, алгоритмы с использованием стека (которые рекурсивны по своей природе) - не единственная возможность при необходимости управлять сразу несколькими вычислительными задачами. Эффективная техника разработки алгоритмов для решения многих задач заключается в использовании реализаций обобщенных очередей, отличающихся от стеков; такие очереди позволяют выбирать следующую задачу в соответствии с каким -либо более субъективным критерием, нежели простой выбор самой последней. Структуры данных и алгоритмы, которые эффективно поддерживают такие операции - основная тема "Очереди с приоритетами и пирамидальная сортировка" , а со многими примерами их применения мы встретимся во время изучения алгоритмов обработки графов в части 7.

Ссылки для части II

Существует множество учебников для начинающих, посвященных структурам данных. Например, в книге Стендиша (Standish) темы связных структур, абстракций данных, стеков и очередей, распределения памяти и создания программ освещаются более подробно, чем здесь. Конечно, классические книги Кернигана и Ритчи (Kernighan -Ritchie) и Страуструпа (Stroustrup) - бесценные источники подробной информации по реализациям на С и С++. Книги Мейерса (Meyers) также содержат полезную информацию о реализациях на C++.

Разработчики PostScript, вероятно, не могли даже и предполагать, что разработанный ими язык будет представлять интерес для людей, которые изучают основные алгоритмы и структуры данных. Сам по себе этот язык не представляет особой сложности, а справочное руководство по нему основательно и доступно.

Парадигма "клиент -интерфейс -реализация " подробно и с множеством примеров описывается в книге Хэнсона (Hanson). Эта книга - замечательный справочник для тех программистов, которые намерены писать надежный и переносимый код для больших систем.

Книги Кнута (Knuth), в особенности 1 -й и 3 -й тома, остаются авторитетным источником информации по свойствам элементарных структур данных. Книги Баеcа -Ятеса (Baeza -Yates) и Гонне (Gonnet) содержат более свежую информацию, подкрепленную внушительным библиографическим перечнем. Книга Седжвика и Флажоле (Sedgewick and Flajolet) подробно освещает математические свойства деревьев.

1. Adobe Systems Incorporated, PostScript Language Reference Manual, second edition, Addison -Wesley, Reading, MA, 1990.

2. R. Baeza -Yates and G. H. Gonnet, Handbook of Algorithms and Data Structures, second edition, Addison -Wesley, Reading, MA, 1984.

3. D. R. Hanson, C Interfaces and Implementations: Techniques for Creating Reusable Software, Addison -Wesley, 1997.

4. Брайан У. Керниган, Деннис М. Ритчи, Язык программирования C (Си), 2 -е издание, ИД "Вильямс", 2008 г.

5. Д.Э. Кнут, Искусство программирования, том 1: Основные алгоритмы, 3 -е издание, ИД "Вильямс", 2008 г.; Д.Э. Кнут, Искусство программирования, том 2: Получисленные алгоритмы, 3 -е издание, ИД "Вильямс", 2008 г.; Д.Э. Кнут, Искусство программирования, том 3. Сортировка и поиск, 2 -е издание, ИД "Вильямс", 2008 г.

6. S. Meyers, Effective C++, second edition, Addison -Wesley, Reading, MA, 1996.

7. S. Meyers, More Effective C++, Addison -Wesley, Reading, MA, 1996.

8. R. Sedgewick and P Flajolet, An Introduction to the Analysis of Algorithms, Addison -Wesley, Reading, MA, 1996.

9. T. A. Standish, Data Structures, Algorithms, and Software Principles in C, Addison -Wesley, 1995.

10. B. Stroustrup, The C++ Programming Language, third edition, Addison -Wesley, Reading MA, 1997.