|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Элементарные структуры данных
Массивы
Возможно, наиболее фундаментальной структурой данных является массив, который определен как примитив в C++ и большинстве других языков программирования. В примерах "Введение" уже встречалось использование массива в качестве основы разработки эффективного алгоритма. В этом разделе вы увидите еще ряд примеров.
Массив является фиксированным набором однотипных данных, которые хранятся в виде непрерывной последовательности. Доступ к данным осуществляется по индексам. Для ссылки на i-й элемент массива используется выражение a[i]. Перед выборкой элемента массива a[i] программист должен занести туда какое-то значение. Кроме того, в языке C++ программист должен сам следить, чтобы индексы были неотрицательны и меньше размера массива. Пренебрежение этими правилами является распространенной ошибкой программирования.
Фундаментальность массивов, как структур данных, заключается в их прямом соответствии системам памяти почти на всех компьютерах. Для извлечения содержимого слова из памяти машинный язык требует указания адреса. Таким образом, всю память компьютера можно рассматривать как массив, где адреса памяти соответствуют индексам. Большинство процессоров машинного языка транслируют программы, использующие массивы, в эффективные программы на машинном языке, в которых осуществляется прямой доступ к памяти. Можно с уверенностью сказать, что доступ к массиву с помощью выражения a[i] требует лишь нескольких машинных команд.
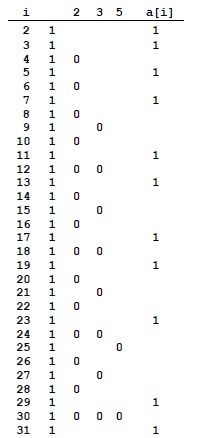
Простой пример использования массива демонстрируется в программе 3.5, которая распечатывает все простые числа, меньшие 10000. Используемый метод восходит к третьему столетию до н.э. и называется решетом Эратосфена (см. рис. 3.1).
Программа 3.5. Решето Эратосфена
Цель программы заключается в присвоении элементам a[i] значения 1, если i простое число, и значения 0 в противном случае. Сначала значение 1 присваивается всем элементам массива. Затем присваивается значение 0 элементам, индексы которых не являются простыми числами (кратны известным простым числам). Если после этого некоторый элемент a[i] сохраняет значение 1, его индекс является простым числом.
Поскольку массив состоит из элементов простейшего типа, принимающих только значения 0 или 1, для экономии памяти было бы лучше использовать массив битов, а не целых чисел. Кроме того, в некоторых средах программирования требуется, чтобы массив был глобальным, если значение N очень велико, либо можно выделять пространство для массива динамически (см. программу 3.6).
#include <iostream.h>
static const int N = 1000;
int main()
{ int i, a[N];
for (i = 2; i < N; i++) a[i] = 1;
for (i = 2; i < N; i++)
if (a[i])
for (int j = i; j*i < N; j++) a[i*j] = 0;
for (i = 2; i < N; i++)
if (a[i]) cout << " " << i;
cout << endl;
}
Для вычисления простых чисел, меньших 32, сначала во все элементы массива заносится значение 1 (второй столбец). Это указывает, что пока не обнаружено ни одно число, которое не является простым (элементы a[0] и a[1] не используются и не показаны). Затем заносится значение 0 в те элементы массива, индексы которых кратны 2, 3 и 5, поскольку они не являются простыми числами. Индексы элементов массива, в которых сохранилось значение 1, являются простыми числами (крайний правый столбец).
Это типичный алгоритм, где используется возможность быстрого доступа к любому элементу массива по его индексу. Реализация содержит четыре цикла, из которых три выполняют последовательный доступ к массиву от первого до последнего элемента. Четвертый цикл выполняет скачки по массиву, через i элементов за один раз. В некоторых случаях последовательная обработка абсолютно необходима, а в других используется просто поскольку она не хуже других методов. Например, первый цикл программы 3.5 можно заменить на
for (i = N-1; i > 1, i--) a[i] = 1;
что никак не отразится на вычислениях. Подобным же образом можно изменить направление внутреннего цикла, либо изменить последний цикл, чтобы печатать простые числа в порядке убывания. Однако нельзя изменить порядок выполнения внешнего цикла основных вычислений, поскольку перед проверкой элемента a[i] на простоту уже должны быть обработаны все целые числа, меньшие i.
Мы не будем подробно анализировать время выполнения программы 3.5, дабы не углубляться в теорию чисел. Однако очевидно, что время выполнения пропорционально
N + N/2 + N/3 + N/5 + N/7 + N/11 + ...
что меньше, чем
N + N/2 + N/3 + N/4 + ... = NHN ~ Nln N.
Одно из отличительных свойств C++ состоит в том, что имя массива генерирует указатель на первый элемент массива (с индексом 0). Более того, возможны простые арифметические операции с указателями: если p является указателем на объект определенного типа, можно записать код, предполагающий последовательное расположение объектов данного типа. При этом для ссылки на первый объект используется запись *p, на второй - *(p+1), на третий - *(p+2) и т.д. Другими словами, записи *(a+i) и a[i] в языке C++ эквивалентны.
Это обеспечивает альтернативный механизм доступа к объектам массивов, который иногда оказывается удобнее индексации. Он чаще всего используется для массивов символов (строк). Мы вернемся к этому вопросу в разделе 3.6.
Подобно структурам, указатели на массивы важны тем, что позволяют эффективно управлять массивами как высокоуровневыми объектами. В частности, указатель на массив можно передать как аргумент функции - это позволяет функции обращаться к объектам массива без необходимости создания копии всего массива. Такая возможность необходима при написании программ, работающих с очень большими массивами. Например, она используется в функциях поиска, рассмотренных в разделе 2.6 "Принципы анализа алгоритмов" . Другие примеры будут приведены в разделе 3.7.
В программе 3.5 предполагается, что размер массива должен быть известен заранее. Чтобы выполнить программу для другого значения N, следует изменить константу N и повторно скомпилировать программу. В программе 3.6 показан другой способ: пользователь может ввести значение N, и программа выведет простые числа, меньшие этой величины. Здесь применены два основных механизма C++, и в обоих массивы передаются в функции в качестве аргументов. Первый механизм обеспечивает передачу аргументов командной строки главным программам в массиве argv с размером argc. Массив argv является составным и включает объекты, которые сами представляют собой массивы (строки). Мы отложим его рассмотрение до раздела 3.7, а пока примем на веру, что переменная N принимает значение, вводимое пользователем при выполнении программы.
Программа 3.6. Динамическое выделение памяти массиву
Для изменения верхнего предела простых чисел, вычисляемых в программе 3.5, необходима повторная компиляция программы. Однако предельное значение можно принимать из командной строки и использовать его для выделения памяти массиву во время выполнения с помощью операции C++ new[]. Например, если скомпилировать программу и ввести в командной строке 1000000, будут получены все целые числа, меньшие миллиона (если компьютер достаточно мощный для таких вычислений). Для отладки программы (с небольшими затратами времени и памяти) достаточно значения 10 0. В дальнейшем мы будем часто использовать этот подход, хотя для краткости не будем выполнять проверку на нехватку памяти.
int main(int argc, char *argv[])
{ int i, N = atoi(argv[1]);
int *a = new int[N];
if (a == 0)
{ cout << "не хватает памяти" << endl; return 0; }
Второй базовый механизм - операция new[], которая во время выполнения выделяет под массив нужный объем памяти и возвращает указатель на массив. В некоторых языках программирования динамическое выделение памяти массивам затруднено либо вообще невозможно. А в некоторых других языках этот процесс выполняется автоматически. Динамическое выделение памяти - важный инструмент в программах, работающих с несколькими массивами, особенно если некоторые из них должны иметь большой размер. Если бы в данном случае не было механизма выделения памяти, нам пришлось бы объявить массив с размером, не меньшим любого допустимого входного параметра. В сложной программе, где может использоваться много массивов, сделать так для каждого из них невозможно. В этой книге мы будем обычно использовать код, подобный коду программы 3.6, по причине его гибкости. Однако в некоторых приложениях, где размер массива известен, вполне применимы простые решения, как в программе 3.5. Массивы не только родственны низкоуровневым средствам доступа к данным памяти в большинстве компьютеров. Они широко распространены еще и потому, что прямо соответствуют естественным методам организации данных в приложениях. Например, массивы прямо соответствуют векторам (математический термин для упорядоченных списков объектов).
Стандартная библиотека C++ содержит класс Vector - абстрактный объект, который допускает индексацию подобно массиву (с необязательной автоматической проверкой соответствия диапазону), но в нем предусмотрена возможность увеличения и уменьшения размера. Это позволяет воспользоваться преимуществами массивов, но возлагать задачи проверки допустимости индексов и управления памятью на систему. Поскольку в этой книге много внимания уделяется быстродействию, мы будем избегать неявных затрат и поэтому чаще использовать массивы, указывая, что в коде могут быть применены и векторы (см. упражнение 3.14).
Программа 3.7 - пример программы моделирования, использующей массивы. В ней моделируется последовательность испытаний Бернулли (Bernoulli trials) - известная абстрактная концепция теории вероятностей. Если подбросить монету N раз, вероятность выпадения k решек составляет
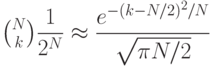
Программа 3.7. Имитация подбрасываний монеты
Если подбросить монету N раз, ожидается выпадение N/2 решек, но в принципе это число может быть любым в диапазоне от 0 до N. Данная программа выполняет эксперимент Mраз, принимая аргументы Mи N из командной строки. Она использует массив f для отслеживания частоты выпадений "i решек" для  , а затем выводит гистограмму результатов эксперимента. Каждые 10 выпадений обозначаются одной звездочкой.
, а затем выводит гистограмму результатов эксперимента. Каждые 10 выпадений обозначаются одной звездочкой.
Основная операция программы - индексация массива по вычисляемым значениям - важный фактор эффективности многих вычислительных процедур.
#include <iostream.h>
#include <stdlib.h>
int heads()
{ return rand() < RAND MAX/2; }
int main(int argc, char *argv[])
{ int i, j, cnt;
int N = atoi(argv[1]), M = atoi(argv[2]);
int *f = new int[N+1];
for (j = 0; j <= N; j + +) f[j] = 0;
for (i = 0; i < M; i++, f[cnt]++)
for (cnt = 0, j = 0; j <= N; j++)
if (heads()) cnt++;
for (j = 0; j <= N; j++)
{ if (f[j] == 0) cout << ".";
for (i = 0; i < f[j]; i += 10) cout << "*";
cout << endl;
}
}
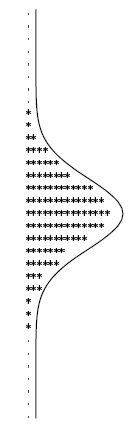
Эта таблица демонстрирует результат выполнения программы 3.7 при = 32 и M = 1000. Имитируется 1000 экспериментов подбрасывания монеты по 32 раза. Количество выпадений решки аппроксимируется нормальной функцией распределения, график которой показан поверх данных.
Здесь используется нормальная аппроксимация - известная кривая в форме колокола. На рис. 3.2 показан результат работы программы 3.7 для 1000 экспериментов подбрасывания монеты по 32 раза. Дополнительные сведения о распределении Бернулли и нормальной аппроксимации можно найти в любом учебнике по теории вероятностей. Эти понятия вновь встретятся нам в "Сбалансированные деревья" . А пока нам интересны вычисления, в которых используются числа как индексы массива для определения частоты выпадений. Способность поддерживать этот вид операций - одно из основных достоинств массивов.
В программах 3.5 и 3.7 индексы массива вычисляются по имеющимся данным. При использовании вычисленного значения для доступа к массиву размером N в некотором смысле с помощью единственной операции обрабатывается N возможных вариантов. Это существенно повышает эффективность, и в дальнейшем мы встретим много алгоритмов, где массивы используются подобным образом.
Массивы можно применять для организации объектов различных типов, а не только целых чисел. В языке C++ можно объявлять массивы любых встроенных либо определяемых пользователем типов (другими словами, составных объектов, объявленных как структуры). В программе 3.8 показано использование массива структур для точек на плоскости - с помощью описания структуры из раздела 3.1. Кроме того, демонстрируется типичное использование массивов: организованное хранение данных для обеспечения быстрого доступа к ним в процессе вычислений.
Между прочим, программа 3.8 также интересна в качестве примера квадратичного алгоритма: в ней выполняется проверка всех пар набора из N элементов данных, в результате чего затрачивается время, пропорциональное N2. В этой книге для подобных алгоритмов мы всегда пытаемся найти более эффективную альтернативу, поскольку с увеличением N данное решение становится неподъемным. Для данного случая в разделе 3.7 будет показано использование составных структур данных, что дает линейное время вычисления.
Программа 3.8. Вычисление ближайшей точки
Эта программа демонстрирует использование массива структур и представляет типичный случай, когда элементы сохраняются в массиве для последующей обработки в процессе некоторых вычислений. Подсчитывается количество пар из N сгенерированных случайным образом точек на плоскости, соединяемых прямой, длина которой меньше d. При этом используется тип данных для точек, описанный в разделе 3.1. Время выполнения составляет O(N2) , поэтому программа не может применяться для больших значений N. Программа 3.20 обеспечивает более быстрое решение.
#include <math.h>
#include <iostream.h>
#include <stdlib.h>
#include "Point.h"
float randFloat()
{ return 1.0*rand()/RAND MAX; }
int main(int argc, char *argv[])
{ float d = atof(argv[2]);
int i, cnt = 0, N = atoi(argv[1]);
point *a = new point[N];
for (i = 0; i < N; i++)
{ a[i].x = randFloat(); a[i].y = randFloat(); }
for (i = 0; i < N; i++)
for (int j = i+1; j < N; j + +)
if (distance(a[i], a[j]) < d) cnt++;
cout << cnt << " пар в радиусе " << d << endl;
}
Подобным образом можно создавать составные типы произвольной сложности: не только массивы структур, но и массивы массивов, либо структуры, содержащие массивы. Эти возможности будут подробно рассматриваться в разделе 3.7. Однако сначала ознакомимся со связными списками, которые служат главной альтернативой массивам при организации коллекций объектов.
Упражнения
- 3.10. Предположим, переменная a объявлена как int a[99]. Определите содержимое массива после выполнения следующих двух операторов:
- for (i = 0; i < 99; i++) a[i] = 98-i;
- for (i = 0; i < 99; i++) a[i] = a[a[i]];
- 3.11. Измените реализацию решета Эратосфена (программа 3.5) для использования массива (1) символов и (2) разрядов. Определите влияние этих изменений на расход памяти и времени, используемых программой.
- 3.12. С помощью решета Эратосфена определите количество простых чисел, меньших N, для N = 103, 104, 105 и 106 .
- 3.13. С помощью решета Эратосфена постройте график зависимости от N количества простых чисел, меньших N, для значений N от 1 до 1000.
- 3.14. Стандартная библиотека C++ в качестве альтернативы массивам содержит тип данных Vector. Узнайте, как использовать этот тип данных в своей системе, и определите его влияние на время выполнения, если заменить в программе 3.5 массив типом Vector.
- 3.15. Эмпирически определите эффект удаления проверки a[i] из внутреннего цикла программы 3.5 для N = 103, 104, 105 и 106 и объясните его.
- 3.16. Напишите программу подсчета количества различных целых чисел, меньших 1000, которые встречаются во входном потоке.
- 3.17. Напишите программу, эмпирически определяющую количество случайных положительных целых, меньших 1000, генерацию которых можно ожидать перед получением повторного значения.
- 3.18. Напишите программу, эмпирически определяющую количество случайных положительных целых, меньших 1000, генерацию которых можно ожидать до получения каждого значения хотя бы один раз.
- 3.19. Измените программу 3.7 для имитации случая, когда решка выпадает с вероятностью p. Выполните 1000 испытаний с 32 подбрасываниями при p = 1/6 для получения выходных данных, которые можно сравнить с рис. 3.2.
-
3.20. Измените программу 3.7 для имитации случая, когда решка выпадает с вероятностью
 . Выполните 1000 испытаний с 32 подбрасываниями для получения выходных данных, которые можно сравнить с
рис.
3.2. Получается классическое распределение Пуассона.
. Выполните 1000 испытаний с 32 подбрасываниями для получения выходных данных, которые можно сравнить с
рис.
3.2. Получается классическое распределение Пуассона.
- 3.21. Измените программу 3.8 для вывода координат пары ближайших точек.
- 3.22. Измените программу 3.8 для выполнения тех же вычислений в в d-мерном пространстве.