|
Здравствуйие! Я хочу пройти курс Введение в принципы функционирования и применения современных мультиядерных архитектур (на примере Intel Xeon Phi), в презентации самостоятельной работы №1 указаны логин и пароль для доступ на кластер и выполнения самостоятельных работ, но войти по такой паре логин-пароль не получается. Как предполагается выполнение самосоятельных работ в этом курсе? |
Самостоятельная работа 4: Оптимизация расчетов на примере задачи вычисления справедливой цены опциона Европейского типа
Введение
Если люди не полагают, что математика проста, то только потому, что они не понимают, как на самом деле сложна жизнь.
Презентацию к лабораторной работе Вы можете скачать здесь.
В данной лабораторной работе мы иллюстрируем некоторые приемы оптимизации вычислений в научных и инженерных приложениях. Известна обывательская точка зрения, что такие приложения возникают исключительно в "классических" областях, связанных с промышленностью и производством, например, в машиностроении. Однако применение высокопроизводительной вычислительной техники не ограничивается исключительно физическими расчетами. Так, область высокопроизводительных вычислений (HPC, high performance computing) включает приложения из биологии, химии, медицины, экономики, финансов и др. В этой работе мы сосредоточим свое внимание на достаточно простых расчетах, возникающих при анализе финансовых рынков и происходящих на них процессах. В наших учебных курсах мы обращаемся к этой теме не первый раз (см. ЛР "…." из курса ПарЧМ) [11.3]. Вызвано это тем, что финансовые расчеты – важная, актуальная, востребованная в индустрии часть области HPC. При этом погружение в модели и методы их анализа требует существенной математической подготовки, а реализация алгоритмов для современной аппаратуры – определенной техники программирования. Упомянутая выше лабораторная работа разрабатывалась как часть курса "Параллельные численные методы" и была ориентирована на изучение методов Монте-Карло, аспектов производительности и параллелизма в использовании генераторов случайных чисел, а также методики использования высокопроизводительных генераторов из библиотеки Intel MKL. В данной работе мы не будем углубляться в методы Монте-Карло (эта тема будет затронута в расширенной версии курса), и рассмотрим более простую задачу – вычисление справедливой цены опциона Европейского типа в том случае, когда эта цена может быть вычислена аналитически. Указанная задача является очень простой с точки зрения программирования (подставил все в формулу и вот он ответ), но позволяет показать, что даже в элементарных программах время работы на современной вычислительной техники может отличаться не просто в разы, а на порядки в зависимости от техники программирования – знания основных приемов оптимизации вычислений и навыков их использования.
В работе шаг за шагом иллюстрируется процесс оптимизации программы для обычных процессоров и ускорителей вычислений Intel Xeon Phi.
Методические указания
Цели и задачи работы
Цель данной работы – изучение некоторых принципов оптимизации вычислений в расчетных программах на примере решения задачи вычисления справедливой цены опциона Европейского типа.
Данная цель предполагает решение следующих основных задач:
- Ознакомление с моделью финансового рынка и базовыми понятиями предметной области.
- Подготовка базовой версии программы для вычисления цены опциона Европейского типа по формуле Блэка–Шоулса.
- Пошаговая оптимизация и распараллеливание программы для Intel Xeon.
- Пошаговая оптимизация и распараллеливание программы для Intel Xeon Phi.
- Анализ результатов оптимизации и распараллеливания.
Структура работы
Работа построена следующим образом: вначале дается краткое описание модели финансового рынка, формулируются основные понятия, приводится их интуитивное описание, способствующее пониманию сути и смысла решаемой прикладной задачи. Далее описывается базовая программная реализация, проводится анализ производительности, шаг за шагом в программу вносятся изменения, иллюстрирующие приемы оптимизации: устранение ненужных преобразований типов, вынос инвариантов, эквивалентные преобразования с заменой "тяжелых" математических функций более "легкими", векторизация вычислений, распараллеливание, "прогрев" – снижение накладных расходов на создание потоков, понижение точности вычислений с плавающей запятой, оптимизация работы с памятью (использование streaming stores). Эффекты от оптимизации демонстрируются как на Intel Xeon, так и на Intel Xeon Phi.
Тестовая инфраструктура
Вычислительные эксперименты проводились с использованием следующей инфраструктуры (таблица 9.1).
| Процессор | 2 восьмиядерных процессора Intel Xeon E5-2690 (2.9 GHz) |
| Сопроцессор | 2 сопроцессора Intel Xeon Phi 7110X (61 ядро) |
| Память | 64 GB |
| Операционная система | Linux CentOS 6.2 |
| Компилятор, профилировщик | Intel Parallel Studio XE 2013 SP1 |
Рекомендации по проведению занятий
Для выполнения лабораторной работы рекомендуется следующая последовательность действий.
- Кратко ввести основные понятия предметной области.
- Сформулировать постановку задачи на лабораторную работу, объяснить цели и задачи работы.
- Продемонстрировать базовую версию кода.
- Пошагово выполнить предлагаемые оптимизации кода, показать эффект от их внедрения, обсудить особенности применения указанных приемов и возможный эффект.
- Сравнить производительность на Xeon и Xeon Phi, предложить студентам самостоятельно проделать некоторые оптимизации (в зависимости от наличия свободного доступа к оборудованию, времени и целей, занятие может быть проведено как в режиме мастер-класса, так и в режиме лабораторной работы).
Оценивание опционов европейского типа
Модель финансового рынка
Рассмотрим эволюционирующий в непрерывном времени финансовый рынок, состоящий из двух типов активов – акции (рисковые активы, S) и облигации (безрисковые активы, B). Для моделирования рынка будем использовать широко распространенную модель Блэка – Шоулса [11.2]. Данная модель после ряда преобразований (см. [11.2]) представляет собой систему стохастических дифференциальных уравнений следующего вида:
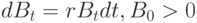 |
( 1) |
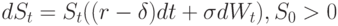 |
( 2) |
Уравнение (1) – обычное дифференциальное уравнение, описывает поведение цены облигации 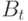 , на изменение которой влияет
, на изменение которой влияет  – процентная ставка (interest rate). Уравнение (2) – стохастическое дифференциальное уравнение, описывающее эволюцию цены акции
– процентная ставка (interest rate). Уравнение (2) – стохастическое дифференциальное уравнение, описывающее эволюцию цены акции 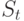 . Наряду с процентной ставкой
. Наряду с процентной ставкой  в уравнении присутствуют ставка дивиденда
в уравнении присутствуют ставка дивиденда  (dividend rate), волатильность
(dividend rate), волатильность  и Винеровский случайный процесс
и Винеровский случайный процесс  . Начальные цены акции и облигации (
. Начальные цены акции и облигации ( и
и 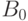 соответственно) считаются заданными.
соответственно) считаются заданными.
Поясним кратко экономический смысл рассмотренной модели. Первое уравнение показывает возможности по вкладыванию средств в безрисковые активы – облигации. Представим, что мы идем в банк и кладем деньги на депозит под некоторый процент, определяемый банком в зависимости от инфляции и состояния дел в банке и на рынке в целом. Второе уравнение моделирует влияние на изменение цены акции (рискового актива) двух групп факторов – детерминированных и случайных. Первое слагаемое – 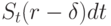 – похоже на правую часть в уравнении (1) с той разницей, что по акциям, в отличие от облигаций, могут платиться дивиденды, что отражается в ставке дивиденда
– похоже на правую часть в уравнении (1) с той разницей, что по акциям, в отличие от облигаций, могут платиться дивиденды, что отражается в ставке дивиденда  . Наибольший интерес представляет слагаемое
. Наибольший интерес представляет слагаемое  , входящее в уравнение аддитивно с рассмотренной частью. Данное слагаемое моделирует влияние случайных, трудно прогнозируемых факторов, на рынок. Волатильность ? характеризует степень случайности процессов на рынке:
, входящее в уравнение аддитивно с рассмотренной частью. Данное слагаемое моделирует влияние случайных, трудно прогнозируемых факторов, на рынок. Волатильность ? характеризует степень случайности процессов на рынке:  – все детерминировано, риск отсутствует. Чем больше
– все детерминировано, риск отсутствует. Чем больше  , тем больше риск (как возможная прибыль, так и возможные убытки). Множитель
, тем больше риск (как возможная прибыль, так и возможные убытки). Множитель 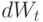 – дифференциал от Винеровского случайного процесса – описывает случайные факторы, влияющие на изменение цены акции в момент времени
– дифференциал от Винеровского случайного процесса – описывает случайные факторы, влияющие на изменение цены акции в момент времени  . Приведем определение Винеровского случайного процесса – математической модели броуновского движения в непрерывном времени:
. Приведем определение Винеровского случайного процесса – математической модели броуновского движения в непрерывном времени:
-
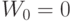 с вероятностью 1.
с вероятностью 1. -
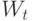 – процесс с независимыми приращениями.
– процесс с независимыми приращениями. -
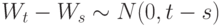 , где
, где 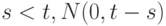 – нормальное распределение с нулевым средним и дисперсией
– нормальное распределение с нулевым средним и дисперсией 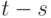 .
. - Траектории процесса
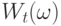 – непрерывные функции времени с вероятностью 1.
– непрерывные функции времени с вероятностью 1.
Для последующей реализации необходимо сделать несколько важных замечаний.
- В формулах и расчетах, приведенных далее, для упрощения будем считать, что
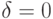 (модель без дивидендов).
(модель без дивидендов). - Если время измеряется в годах, то все рассмотренные процентные ставки участвуют в уравнениях как числа от 0 до 1 – проценты годовых, выраженные в долях.
- Будем считать, что все процентные ставки постоянны – не зависят от времени.
- В рамках предположения о постоянстве процентных ставок система дифференциальных уравнений (1), (2) имеет аналитическое решение. В противном случае, систему приходится решать численно одним из известных методов (метод Эйлера, метод Рунге – Кутты и т.д.). При построении разностной схемы единственное отличие от ОДУ заключается в том, что каждое приращение винеровского случайного процесса моделируется случайным числом, полученным из N(0, t – s).
Итак, при сделанных предположениях система имеет аналитическое решение. В частности, решение уравнения (2) выглядит следующим образом:
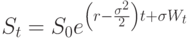 |
( 3) |


