Базисные схемы обработки информации
Схема вычисления инвариантной функции
Общая схема итерации значительно упрощается для случая вычисления значений инвариантных функций.
Определение 7.3.
Пусть  — некоторое множество,
— некоторое множество, 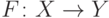 — заданная
на нем функция, а
— заданная
на нем функция, а  — предикат такой, что
— предикат такой, что 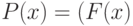 легко вычислить ).
Обозначим через
легко вычислить ).
Обозначим через 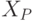 то подмножество множества
то подмножество множества  , где
, где 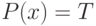 .
Если существует преобразование
.
Если существует преобразование  такое, что
такое, что  , то функция
, то функция  называется
называется  -инвариантной или просто инвариантной
функцией.
-инвариантной или просто инвариантной
функцией.
Простейшим примером инвариантной функции является хорошо известная еще
из средней школы функция 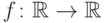 ,
,  . Она является
. Она является  -инвариантной
относительно преобразования
-инвариантной
относительно преобразования  ,
,  .
.
Наибольший общий делитель двух целых чисел (greatest common divisor, 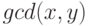 или просто
или просто  ) инвариантен
относительно
преобразования
) инвариантен
относительно
преобразования  ,
задаваемого формулой
,
задаваемого формулой
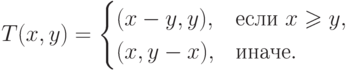
Доказательство этого факта, основанное на основной теореме арифметики о
разложении числа на простые множители, является достаточно простым и
оставляется читателю. Обратите только внимание на то, что функция 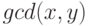 не определена в точке
не определена в точке 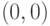 .
.
Для вычисления значения  -инвариантной функции
-инвариантной функции  в точке
в точке 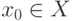 применяется следующая схема.
применяется следующая схема.
Схема вычисления инвариантной функции.
Многократно выполняется преобразование  ,
дающее последовательность точек
,
дающее последовательность точек 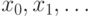 Если
очередная точка
Если
очередная точка 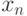 попадaет в подмножество
попадaет в подмножество 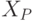 , то
итерации завершаются.
По определению инвариантной функции
, то
итерации завершаются.
По определению инвариантной функции  легко вычисляется и
совпадает с
искомым
легко вычисляется и
совпадает с
искомым 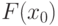 .
.
Рисунок 7.4 содержит графическую иллюстрацию этой схемы.
Схема вычисления инвариантной функции значительно облегчает проектирование
программы "S0;while(e)S;S1;", так как нам изначально известны инвариант 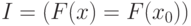 и условие продолжения цикла
и условие продолжения цикла 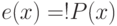 .
Тело цикла S конструируется, как программная реализация известного
преобразования
.
Тело цикла S конструируется, как программная реализация известного
преобразования  , а написание S1, вычисляющей
, а написание S1, вычисляющей  , не может
представлять трудностей в силу самого определения инвариантной функции.
, не может
представлять трудностей в силу самого определения инвариантной функции.
В качестве иллюстрации применения схемы вычисления инвариантной функции рассмотрим следующую задачу.
Задача 7.4. Напишите программу, находящую наибольший общий делитель 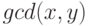 двух целых неотрицательных чисел
двух целых неотрицательных чисел  и
и  , не равных одновременно нулю.
Воспользуйтесь следующими свойствами наибольшего общего делителя
(не забудьте научиться доказывать все
эти свойства):
, не равных одновременно нулю.
Воспользуйтесь следующими свойствами наибольшего общего делителя
(не забудьте научиться доказывать все
эти свойства):
-
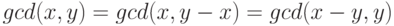 ,
, -
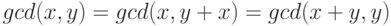 ,
, -
 ,
,  ,
, 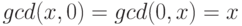 .
.
Решение Если через 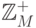 обозначить множество всех
неотрицательных
целых чисел, представимых в ЭВМ, то
обозначить множество всех
неотрицательных
целых чисел, представимых в ЭВМ, то  ,
,  ,
,  ,
,  . В качестве преобразования
. В качестве преобразования 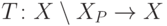 можно взять
можно взять
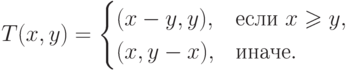
Таким образом, нам известны инвариант  и
условие продолжения
и
условие продолжения  . Начальные
присваивания S0 в
данном случае не нужны, тело цикла S пишется по
определению
. Начальные
присваивания S0 в
данном случае не нужны, тело цикла S пишется по
определению  , a
программа S1, вычисляющая
, a
программа S1, вычисляющая 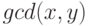 для
для  , реализуется с
помощью справедливой для этих значений аргумента формулы
, реализуется с
помощью справедливой для этих значений аргумента формулы  .
.
Текст программы
public class Gcd {
public static void main(String[] args) throws Exception {
int x = Xterm.inputInt("x -> ");
int y = Xterm.inputInt("y -> ");
Xterm.print("gcd(" + x + "," + y + ") =");
while ( (x != 0) && (y != 0) ) {
if (x >= y) x -= y;
else y -= x;
}
Xterm.println(" " + (x+y));
}
}Обратите внимание на тот факт, что в построенной программе не понадобилось
наличие переменной, соответствующей значению инвариантной функции 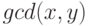 .
.
Рассмотрим еще одну задачу.
Задача 7.5. Напишите программу, перемножающую два целых числа, одно из
которых неотрицательно, без использования операции умножения. Точные
пред- и постусловия требуемой программы, временная
сложность которой не должна превосходить 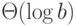 , таковы:
, таковы:  ,
, 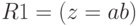 . При написании программы величины
. При написании программы величины  и
и  изменять не
разрешается. Воспользуйтесь тем, что
функция
изменять не
разрешается. Воспользуйтесь тем, что
функция  ,
,  является инвариантной
относительно преобразования
является инвариантной
относительно преобразования  , задаваемого
формулой
, задаваемого
формулой
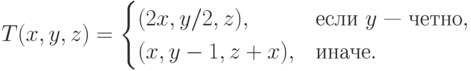
В данном случае 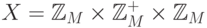 ,
,  ,
, 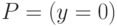 ,
,  .
Функция
.
Функция  и преобразование
и преобразование  заданы в условии
задачи.
заданы в условии
задачи.
Таким образом, нам известны инвариант  и
условие продолжения
и
условие продолжения  . Начальные присваивания S0
очевидны ( "x=a; y=b; z=0;" ),
тело цикла S пишется по определению
. Начальные присваивания S0
очевидны ( "x=a; y=b; z=0;" ),
тело цикла S пишется по определению  , a
программа S1, вычисляющая
, a
программа S1, вычисляющая  для
для  , в
данном случае вырождается в пустой оператор ";", так как для этих значений
аргумента
, в
данном случае вырождается в пустой оператор ";", так как для этих значений
аргумента 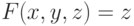 . В результате получаем уже знакомую нам
программу.
. В результате получаем уже знакомую нам
программу.
Текст программы
public class MulInv {
public static void main(String[] args) throws Exception {
int a = Xterm.inputInt("a -> ");
int b = Xterm.inputInt("b -> ");
int x = a, y = b, z = 0;
while (y > 0) {
if ((y&1) == 0) {
y >>>= 1; x += x;
} else {
y -= 1; z += x;
}
}
Xterm.println("a * b = " + z);
}
}

