Базисные схемы обработки информации
Задачи для самостоятельного решения
При решении задач на рекурсию необходимо обосновать как то, почему программа заканчивает работу, так и то, почему после ее завершения будет получен требуемый результат.
При использовании схемы вычисления инвариантной функции
необходимо указать
множества  ,
,  и
и 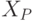 , функцию
, функцию  и преобразование
и преобразование  (см. определение инвариантной функции) и
объяснить программную реализацию преобразования
(см. определение инвариантной функции) и
объяснить программную реализацию преобразования  .
.
Задача 7.7. Напишите рекурсивную программу, печатающую значение производной
многочлена степени  в
заданной точке
в
заданной точке  . Коэффициенты многочлена хранятся в массиве
. Коэффициенты многочлена хранятся в массиве  в порядке убывания степеней и являются целыми числами, так же как и
значение
в порядке убывания степеней и являются целыми числами, так же как и
значение  . Величины
. Величины  ,
,  и элементы массива
и элементы массива  изменять в
программе нельзя.
изменять в
программе нельзя.
Указание
Пусть  .
Продифференцируем по
.
Продифференцируем по  равенство
равенство  и подставим затем
и подставим затем  . Мы получим
следующие соотношения:
. Мы получим
следующие соотношения:
 ,
,
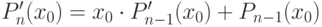 .
.
Воспользовавшись ими и формулами
 ,
,
 ,
,
легко определить рекурсивную функцию неотрицательного целого аргумента  ,
, 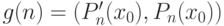 для вычисления которой и пишется программа.
для вычисления которой и пишется программа.
Задача 7.8. Напишите программу, возводящую целое число в целую
неотрицательную степень. Точные
пред- и постусловия требуемой программы таковы:  ,
, 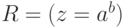 .
При написании программы величины
.
При написании программы величины  и
и  изменять не
разрешается, следует использовать инвариант
изменять не
разрешается, следует использовать инвариант  и ограничивающую функцию
и ограничивающую функцию  .
.
Задача 7.9. Напишите программу, находящую наибольший общий делитель 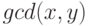 двух целых неотрицательных чисел
двух целых неотрицательных чисел  и
и  , не равных одновременно нулю.
Воспользуйтесь следующим свойством наибольшего общего
делителя (докажите его!):
, не равных одновременно нулю.
Воспользуйтесь следующим свойством наибольшего общего
делителя (докажите его!):

 позволяет найти остаток от деления
позволяет найти остаток от деления  на
на  .
.Задача 7.10. Напишите программу, возводящую целое число в целую
неотрицательную степень. Точные
пред- и постусловия требуемой программы таковы:  ,
, 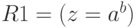 .
При написании программы величины
.
При написании программы величины  и
и  изменять не
разрешается. Воспользуйтесь тем, что
функция
изменять не
разрешается. Воспользуйтесь тем, что
функция  ,
, 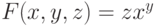 является инвариантной
относительно преобразования
является инвариантной
относительно преобразования  , задаваемого
формулой
, задаваемого
формулой  .
.
Задача 7.11. Напишите программу, находящую наибольший общий делитель 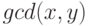 двух целых неотрицательных чисел
двух целых неотрицательных чисел  и
и  , не равных одновременно нулю.
Программа должна иметь временную сложность порядка
, не равных одновременно нулю.
Программа должна иметь временную сложность порядка  и не использовать операций деления и нахождения остатка от деления
(допустимо деление пополам, реализуемое с помощью операции сдвига).
Воспользуйтесь следующими свойствами наибольшего общего
делителя (докажите их!):
и не использовать операций деления и нахождения остатка от деления
(допустимо деление пополам, реализуемое с помощью операции сдвига).
Воспользуйтесь следующими свойствами наибольшего общего
делителя (докажите их!):
 ,
, 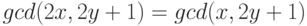 .
.
Указание
Воспользуйтесь инвариантностью функции 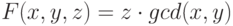 относительно
следующего преобразования
относительно
следующего преобразования  :
:

 ,-инвариантность функции
,-инвариантность функции  .
.
