Предсказание финансовых временных рядов

Методика предсказания временных рядов

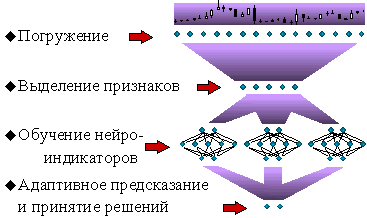
Для начала обрисуем общую схему нейросетевого предсказания временных рядов (рисунок 8.1).

Рис. 8.1. Схема технологического цикла предсказаний рыночных временных рядов

Далее в этой лекции мы кратко обсудим все этапы этой технологической цепочки. Хотя общие принципы нейро-моделирования применимы к данной задаче в полном объеме, предсказание финансовых временных рядов имеет свою специфику. Именно эти отличительные черты и будут в большей мере затронуты в этой лекции.

Метод погружения. Теорема Такенса

Начнем с этапа погружения. Как мы сейчас убедимся, несмотря на то, что предсказания, казалось бы, являются экстраполяцией данных, нейросети, на самом деле, решают задачу интерполяции, что существенно повышает надежность решения. Предсказание временного ряда сводится к типовой задаче нейроанализа - аппроксимации функции многих переменных по заданному набору примеров - с помощью процедуры погружения ряда в многомерное пространство (Weigend, 1994). Например, -мерное лаговое пространство ряда 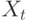состоит из значений ряда в последовательные моменты времени: .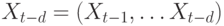

Для динамических систем доказана следующая теорема Такенса. Если временной ряд порождается динамической системой, т. е. значения 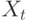есть произвольная функция состояния такой системы, существует такая глубина погружения (примерно равная эффективному числу степеней свободы данной динамической системы), которая обеспечивает однозначное предсказание следующего значения временного ряда (Sauer, 1991). Таким образом, выбрав достаточно большое можно гарантировать однозначную зависимость будущего значения ряда от его предыдущих значений: 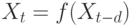, т. е. предсказание временного ряда сводится к задаче интерполяции функции многих переменных. Нейросеть далее можно использовать для восстановления этой неизвестной функции по набору примеров, заданных историей данного временного ряда.

Напротив, для случайного ряда знание прошлого ничего не дает для предсказания будущего. Поэтому, согласно теории эффективного рынка, разброс предсказываемых значений ряда на следующем шаге при погружении в лаговое пространство не изменится.

Отличие хаотической динамики от стохастической (случайной), проявляющееся в процессе погружения, иллюстрирует рисунок 8.2.

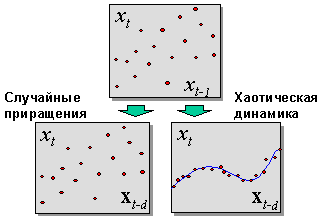
Рис. 8.2. Проявляющееся по мере погружения ряда различие между случайным процессом и хаотической динамикой

Эмпирические свидетельства предсказуемости финансовых рядов

Метод погружения позволяет количественно измерить предсказуемость реальных финансовых инструментов, т. е. проверить или опровергнуть гипотезу эффективности рынка. Согласно последней, разброс точек по всем координатам лагового пространства одинаков (если они - одинаково распределенные независимые случайные величины). Напротив, хаотическая динамика, обеспечивающая определенную предсказуемость, должна приводить к тому, что наблюдения будут группироваться вблизи некоторой гиперповерхности 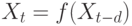, т. е. экспериментальная выборка формирует некоторое множество размерности меньшей, чем размерность всего лагового пространства.

Для измерения размерности можно воспользоваться следующим интуитивно понятным свойством: если множество имеет размерность , то при разбиении его на все более мелкие покрытия кубиками со стороной , число таких кубиков растет как 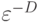. На этом факте основывается определение размерности множеств уже знакомым нам методом box-counting. Размерность множества точек определяется по скорости возрастания числа ячеек (boxes), содержащих все точки множества^{2Вообще говоря можно определить целое семейство т.н. размерностей Реньи: , определяемых через относительные числа заполнения ячеек . Причем называют размерностью Хаусдорфа, - информационной, а - корреляционной размерностями. Чем выше степень , тем меньше эффективное число ячеек, и соответственно - тем меньше размерность. Для сопоставимости с другими применениями box-counting в данных лекциях мы будем опираться на информационную размерность , численно равную энтропии, деленной на число бит данной степени разрешения.} Для ускорения алгоритма размеры берут кратными 2, т.е. масштаб разрешения измеряется в битах.

В качестве примера типичного рыночного временного ряда возьмем такой известный финансовый инструмент, как индекс котировок акций 500 крупнейших компаний США, S&P500, отражающий среднюю динамику цен на Нью-Йоркской бирже. рисунок 8.3 показывает динамику индекса на протяжении 679 месяцев. Размерность (информационная) приращений этого ряда, подсчитанная методом box-counting, показана на следующем рисунке ( рисунок 8.4).

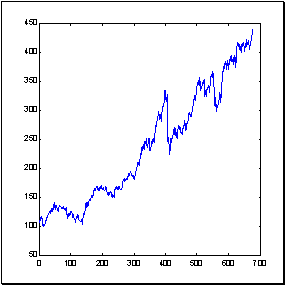
Рис. 8.3. Временной ряд 679 значений индекса S&P500, используемый на протяжении данной лекции в качестве примера

Рис. 8.4. Информационая размерность приращений ряда S&P500

Как следует из последнего рисунка, в 15-мерном пространстве погружения экспериментальные точки формируют множество размерности примерно 4. Это значительно меньше, чем 15, что мы получили бы исходя из гипотезы эффективного рынка, считающей ряд приращений независимыми случайными величинами.

Таким образом, эмпирические данные убедительно свидетельствуют о наличии некоторой предсказуемой составляющей в финансовых временных рядах, хотя здесь и нельзя говорить о полностью детерминированной хаотической динамике^{3График размерностей с ростом глубины погружения не выходит на насыщение, которое зафиксировало бы существование замкнутой детерминистической системы} Значит попытки применения нейросетевого анализа для предсказания рынков имеют под собой веские основания.

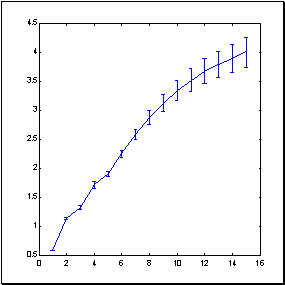
Заметим, однако, что теоретическая предсказуемость вовсе не гарантирует достижимость практически значимого уровня предсказаний. Количественную оценку предсказуемости конкретных рядов дает измерение кросс-энтропии, также возможное с помощью методики box-counting. Для примера приведем измерения предсказуемости приращений индекса S&P500 в зависимости от глубины погружения^{4График размерностей с ростом глубины погружения не выходит на насыщение, которое зафиксировало бы существование замкнутой детерминистической системы} Кросс-энтропия 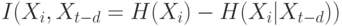, график которой приведен ниже ( рисунок 8.5), измеряет дополнительную информацию о следующем значении ряда, обеспеченную знанием прошлых значений этого ряда.

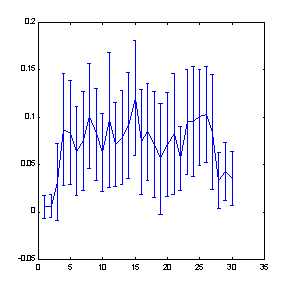
Рис. 8.5. Предсказуемость знака приращений ряда индекса S&P500 в зависимости от глубины погружения (ширины "окна"). Увеличение глубины погружения свыше 25 сопровождается снижением предсказуемости

Далее в этой лекции мы оценим какой доход в принципе способен обеспечить такой уровень предсказуемости.

Формирование входного пространства признаков

Как иллюстрирует рисунок 8.5, увеличение ширины окна погружения ряда приводит в конце концов к понижению предсказуемости - когда повышение размерности входов уже не компенсируется увеличением их информативности. В этом случае, когда размерность лагового пространства слишком велика для данного количества примеров, приходится применять специальные методики формирования пространства признаков с меньшей размерностью. Способы выбора признаков и/или увеличения числа доступных примеров, специфичные для финансовых временных рядов будут описаны ниже.

Выбор функционала ошибки

Для обучения нейросети недостаточно сформировать обучающие наборы входов-выходов. Необходимо также определить ошибку предсказаний сети. Среднеквадратичная ошибка, используемая по умолчанию в большинстве нейросетевых приложений, не имеет большого "финансового смысла" для рыночных рядов. Поэтому в отдельном разделе мы рассмотрим специфичные для финансовых временных рядов функции ошибки и покажем их связь с возможной нормой прибыли.

Например, для выбора рыночной позиции надежное определение знака изменения курса более важно, чем понижение среднеквадратичного отклонения. Хотя эти показатели и связаны между собой, сети оптимизированные по одному из них будут давать худшие предсказания другого. Выбор адекватной функции ошибки, как мы покажем далее в этой лекции, должен опираться на некую идеальную стратегию и диктоваться, например, максимизацией прибыли (или минимизацией возможных убытков).

Обучение нейросетей

Основная специфика предсказания временных рядов лежит в области предобработки данных. Процедура обучения отдельных нейросетей стандартна. Как всегда, имеющиеся примеры разбиваются на три выборки: обучающая, валидационная и тестовая. Первая используется для обучения, вторая - для выбора оптимальной архитектуры сети и/или для выбора момента остановки обучения. Наконец, третья, которая вообще не использовалась в обучении, служит для контроля качества прогноза обученной нейросети.

Однако, для сильно зашумленных финансовых рядов существенный выигрыш в надежности предсказаний способно дать использование комитетов сетей. Обсуждением этой методики мы и закончим данную лекцию.

В литературе имеются свидетельства улучшения качества предсказаний за счет использования нейросетей с обратными связями. Такие сети могут обладать локальной памятью, сохраняющей информацию о более далеком прошлом, чем то, что в явном виде присутствует во входах. Рассмотрение таких архитектур, однако, увело бы нас слишком далеко от основной темы, тем более, что существуют альтернативные способы эффективного расширения "горизонта" сети, за счет специальных способов погружения ряда, рассмотренных ниже.