Обучение без учителя: Сжатие информации

Упорядочение нейронов: топографические карты

До сих пор нейроны выходного слоя были неупорядочены: положение нейрона-победителя в соревновательном слое не имело ничего общего с координатами его весов во входном пространстве. Оказывается, что небольшой модификацией соревновательного обучения можно добиться того, что положение нейрона в выходном слое будет коррелировать с положением прототипов в многомерном пространстве входов сети: близким нейронам будут соответствовать близкие значения входов. Тем самым, появляется возможность строить топографические карты чрезвычайно полезные для визуализации многомерной информации. Обычно для этого используют соревновательные слои в виде двумерных сеток. Такой подход сочетает квантование данных с отображением, понижающим размерность. Причем это достигается с помощью всего лишь одного слоя нейронов, что существенно облегчает обучение.

Алгоритм Кохонена

В 1982 году финский ученый Тойво Кохонен (Kohonen, 1982) предложил ввести в базовое правило соревновательного обучения информацию о расположении нейронов в выходном слое. Для этого нейроны выходного слоя упорядочиваются, образуя одно- или двумерные решетки. Т. е. теперь положение нейронов в такой решетке маркируется векторным индексом . Такое упорядочение естественым образом вводит расстояние между нейронами 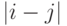в слое. Модифицированное Кохоненом правило соревновательного обучения учитывает расстояние нейронов от нейрона-победителя:

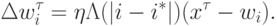
Функция соседства равна единице для нейрона-победителя с индексом и постепенно спадает с расстоянием, например по закону . Как темп обучения , так и радиус взаимодействия нейронов постепенно уменьшаются в процессе обучения, так что на конечной стадии обучения мы возвращаемся к базовому правилу адаптации весов только нейронов-победителей.

В отличие от "газоподобной" динамики обучения при индивидуальной подстройке прототипов (весов нейронов), обучение по Кохонену напоминает натягивание эластичной сетки прототипов на массив данных из обучающей выборки. По мере обучения эластичность сети постепенно увеличивается, чтобы не мешать окончательной тонкой подстройке весов.

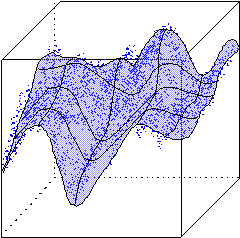
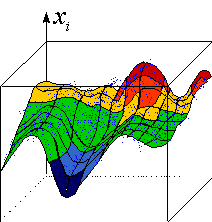
Рис. 4.12. Двумерная топографическая карта набора трехмерных данных. Каждая точка в трехмерном пространстве попадает в свою ячейку сетки имеющую координату ближайшего к ней нейрона из двумерной карты

В результате такого обучения мы получаем не только квантование входов, но и упорядочивание входной информации в виде одно- или двумерной карты. Каждый многомерный вектор имеет свою координату на этой сетке, причем чем ближе координаты двух векторов на карте, тем ближе они и в исходном пространстве. Такая топографическая карта дает наглядное представление о структуре данных в многомерном входном пространстве, геометрию которого мы не в состоянии представить себе иным способом. Визуализация многомерной информации является главным применением карт Кохонена.

Заметим, что в согласии с общим житейским принципом "бесплатных обедов не бывает", топографические карты сохраняют отношение близости лишь локально: близкие на карте области близки и в исходном пространстве, но не наоборот (рисунок 4.13). В общем случае не существует отображения, понижающего размерность и сохраняющего отношения близости глобально.

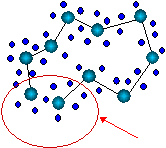
Рис. 4.13. Пример одномерной карты двумерных данных. Стрелкой показана область нарушения непрерывности отображения: близкие на плоскости точки отображаются на противоположные концы карты

Удобным инструментом визуализации данных является раскраска топографических карт, аналогично тому, как это делают на обычных географических картах. Каждый признак данных порождает свою раскраску ячеек карты - по величине среднего значения этого признака у данных, попавших в данную ячейку.

Рис. 4.14. Раскраска топографической карты, индуцированная i-ой компонентой входных данных

Собрав воедино карты всех интересующих нас признаков, получим топографический атлас, дающий интегральное представление о структуре многомерных данных. Далее в этой книге мы рассмотрим практическое применение этой методики к анализу балансовых отчетов и предсказанию банкротств.

Сети радиального базиса

Самообучающиеся сети, рассмотренные в этой лекции, широко используются для предобработки данных, например при распознавании образов в пространстве очень большой размерности. В этом случае для того, чтобы процедура обучения с учителем была эффективна, требуется сначала сжать входную информацию тем или иным способом: либо выделить значимые признаки, понизив размерность, либо произвести квантование данных. Первый путь просто понижает число входов персептрона. Второй же способ требует отдельного рассмотрения, поскольку лежит в основе очень популярной архитектуры - сетей радиального базиса (radial basis functions - RBF).

Аппроксиматоры с локальным базисом

Сеть радиального базиса напоминают персептрон с одним скрытым слоем, осуществляя нелинейное отображение : 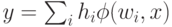, являющееся линейной комбинацией базисных функций. Но в отличие от персептронов, где эти функции зависели от проекций на набор гиперплоскостей 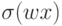, в сетях радиального базиса используются функции (чаще всего - гауссовы), зависящие от расстояний до опорных центров:

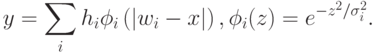
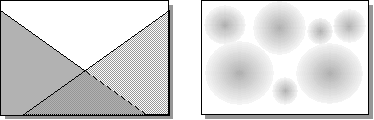
Как тот, так и другой набор базисных функций обеспечивают возможность аппроксимации любой непрерывной функции с произвольной точностью. Основное различие между ними в способе кодирования информации на скрытом слое. Если персепторны используют глобальные переменные (наборы бесконечных гиперплоскостей), то сети радиального базиса опираются на компактные шары, окружающие набор опорных центров (рисунок 4.15).

Рис. 4.15. Глобальная (персептроны) и локальная (сети радиального базиса) методы аппроксимации

В первом случае в аппроксимации в окрестности любой точки участвуют все нейроны скрытого слоя, во втором - лишь ближайшие. Как следствие такой неэффективности, в последнем случае количество опорных функций, необходимых для аппроксимации с заданной точностью, возрастает экспоненциально с размерностью пространства. Это основной недостаток сетей радиального базиса. Основное же их преимущество над персептронами - в простоте обучения.

Гибридное обучение

Относительная автономность базисных функций позволяет разделить обучение на два этапа. На первом этапе обучается первый - соревновательный - слой сети, осуществляя квантование данных. На втором этапе происходит быстрое обучение второго слоя матричными методами, т. к. нахождение коэффициентов второго слоя представляет собой линейную задачу.

Подобная возможность раздельного обучения слоев является основным достоинством сетей радиального базиса. В целом же, области применимости персептронов и сетей радиального базиса коррелируют с найденными выше областями эффективности квантования и понижения размерности (см. рисунок 4.11).

Выводы

В этой лекции мы познакомились со вторым из двух главных типов обучения - обучением без учителя. Этот режим обучения чрезвычайно полезен для предобработки больших массивов информации, когда получить экспертные оценки для обучения с учителем не представляется возможным. Самообучающиеся сети способны выделять оптимальные признаки, формируя относительно малоразмерное пространство признаков, без чего иногда невозможно качественное распознавание образов. Таким образом, оба типа обучения удачно дополняют друг друга. Кроме того, как мы убедились на примере сетей с узким горлом, между этими типами обучения существует тесная взаимосвязь: если посмотреть на ситуацию под определенным углом зрения, соответствующие правила обучения подчас просто совпадают.