|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Методы повышения экономической эффективности ПКС на основе моделирования и оптимизации внутрикорпоративных потоков
В задаче краткосрочного планирования простейшего предприятия требуется найти план функционирования на годовом периоде, обеспечивающий максимум продаж, при условии, что известны:
- максимальные продажи (рынок)
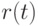 на периоде планирования;
на периоде планирования; - состояние предприятия в начале периода планирования;
- параметры предприятия - оборачиваемость запаса товаров
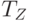 , период отсрочки оплаты поставок
, период отсрочки оплаты поставок 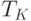 и величина собственных средств
и величина собственных средств  .
.
Для разработки численного метода и получения решений необходима формализация задачи. Обсуждения требует задание состояния предприятия в начале периода планирования. Очевидно, это состояние определяется значениями шести переменных величин в начальный момент планирования  , характеризующих движение средств, потоков и источников средств предприятия, а именно:
, характеризующих движение средств, потоков и источников средств предприятия, а именно:

Однако этого недостаточно, поскольку поток оплаты - это поток поставок, сдвинутый по оси времени вправо на отрезок времени 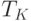 . Следовательно, начальное состояние предприятия необходимо характеризовать еще и заданием совокупности значений функции оплаты поставок на отрезке
. Следовательно, начальное состояние предприятия необходимо характеризовать еще и заданием совокупности значений функции оплаты поставок на отрезке ![t_{0}, t_{0} + T_{K}]](/sites/default/files/tex_cache/e5c0172017a93f8d210e400e548896a4.png) , непосредственно примыкающем к началу периода планирования:
, непосредственно примыкающем к началу периода планирования:
![f_{opt}(t)|_{t \in [t_0,t_0 + T_к]}](/sites/default/files/tex_cache/f8db3c1c8301def6e39bd3b850a5eb9a.png)
Очевидно, задание этой совокупности значений представляет собой учет предыстории функционирования предприятия в моменты времени, предшествующие периоду планирования.
В формализованном виде задача краткосрочного планирования простейшего предприятия формулируется следующим образом.
Задано:
- период планирования
![[t_{0}, t_{pl}]](/sites/default/files/tex_cache/ddc2903b057afe5fc531285f698f81b8.png) , где
, где  - начальный момент периода,
- начальный момент периода, 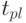 - конечный момент;
- конечный момент; - максимальные продажи (рынок) на периоде планирования
![r(t)|_{t \in [t_0,t_{p1}]}](/sites/default/files/tex_cache/80ff0ee2adc6140587d79a3794feea02.png)
( 5.54) - состояние предприятия в начальный момент
![Z(t_0),D(t_0),K(t_0),f_{pros}(t_0),f_{pos}(t_0),f_{op1}(t_0)|_{t \in [t_0,t_0 + T_к]}](/sites/default/files/tex_cache/11042b6655505b6414d64b54ccd6c505.png)
( 5.55) - значения параметров
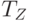 ,
, 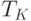 и
и  . Найти: поставки и продажи на периоде планирования
. Найти: поставки и продажи на периоде планирования![f_{pos}(t)|_{t \in [t_0,t_{p1}]}](/sites/default/files/tex_cache/dc741df013e880f6daf89f957341de46.png)
( 5.56) ![f_{pros}(t)|_{t \in [t_0,t_{p1}]}](/sites/default/files/tex_cache/bd3cb8b053a34dbd439b8836a106281c.png)
( 5.57) удовлетворяющие соотношениям (5.16)-(5.25) и обеспечивающие максимум суммарных продаж в течение периода планирования
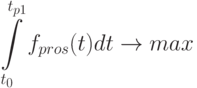
( 5.58)
В задаче искомыми функциями являются интенсивности потоков поставок и продаж, тогда как оплата и функции изменения средств и источников таковыми не считаются. В части потока оплаты причина этого в том, что если решение задачи найдено, то поставки по (5.56) удовлетворяют равенству (5.18) из системы (5.16)-(5.25), по которому оплаты находятся сдвигом функции поставок по оси времени. Также нет необходимости рассматривать в качестве независимых искомых функций изменения средств и источников, поскольку они находятся по найденным потокам как результат притоков и оттоков на периоде планирования по выражениям (5.19)-(5.21).
Разработка и техника применения численного метода решения задачи представлена ниже. Метод назван методом моделирования и оптимизации внутрипроизводственных потоков предприятий; основан на имитационном моделировании и многомерной поисковой оптимизации и реализован в известной программной системе Excel.
Имитационное моделирование осуществляется с постоянным шагом по времени, равным одной неделе, с помощью электронной таблицы, в которой каждому шагу соответствует столбец ячеек. Формулы электронной таблицы моделируют процессы изменения во времени интенсивностей потоков, величин средств и их источников согласно соотношениям математической модели (5.16)-(5.25). Искомые функции поставок и продаж, оптимизация которых требуется в задаче, представляются в электронной таблице в виде последовательности независимых числовых значений с недельным шагом, то есть в виде двух строк. Вся совокупность этих независимых числовых значений выступает в качестве варьируемой и оптимизируется градиентными методами по критерию максимума продаж с помощью штатного поискового оптимизатора системы Excel (в переводе - "Поиск решения", в оригинале - "Solver"). На каждом шаге поисковой оптимизации автоматически проверяется выполнение неравенств математической модели (5.16)-(5.25). Для этого они задаются при настройке оптимизатора в качестве его ограничений. Возможность применения многомерного поискового оптимизатора для поиска оптимальных процессов изменения переменных величин во времени обусловлена значительностью возможного
числа независимых варьируемых величин - до 120. В рассматриваемой задаче в случае годового периода планирования и двух искомых потоков, при 48 рабочих неделях в году количество независимых варьируемых величин составляет 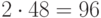 , что меньше максимально допустимого. Продолжительность поиска до получения оптимального решения колеблется в пределах от десятков секунд до нескольких минут, что позволяет достаточно эффективно исследовать задачу при различных значениях параметров.
, что меньше максимально допустимого. Продолжительность поиска до получения оптимального решения колеблется в пределах от десятков секунд до нескольких минут, что позволяет достаточно эффективно исследовать задачу при различных значениях параметров.
Получение оптимальных численных решений задачи представляет интерес для случая перехода к пониженному рынку, то есть на участке 4 и далее после момента 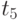 (см.
рис. 5.5). Причина этого в том, что оптимальное планирование в случае перехода от продаж, меньших, чем максимальные
(
(см.
рис. 5.5). Причина этого в том, что оптимальное планирование в случае перехода от продаж, меньших, чем максимальные
( 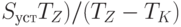 к участку с повышенным рынком, исследовано выше на примере перехода от участка 3 к участку 4 и заключается в кратковременной поставке партии на границе участков. Величина этой партии может находиться по диаграмме (
рис. 5.5, в) как разность проекций изображающих точек на горизонтальную ось. Однако, учитывая выясненную необходимость иметь на участке 4 некоторый запас денежных средств, величина партии должна быть уменьшена в расчете на некоторый "недобор"
к участку с повышенным рынком, исследовано выше на примере перехода от участка 3 к участку 4 и заключается в кратковременной поставке партии на границе участков. Величина этой партии может находиться по диаграмме (
рис. 5.5, в) как разность проекций изображающих точек на горизонтальную ось. Однако, учитывая выясненную необходимость иметь на участке 4 некоторый запас денежных средств, величина партии должна быть уменьшена в расчете на некоторый "недобор" 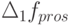 (см.
рис. 5.7, в). Поэтому численные решения изучались применительно к случаю падения рынка, когда на участке 4 предприятие функционирует с некоторым "недобором" продаж.
(см.
рис. 5.7, в). Поэтому численные решения изучались применительно к случаю падения рынка, когда на участке 4 предприятие функционирует с некоторым "недобором" продаж.
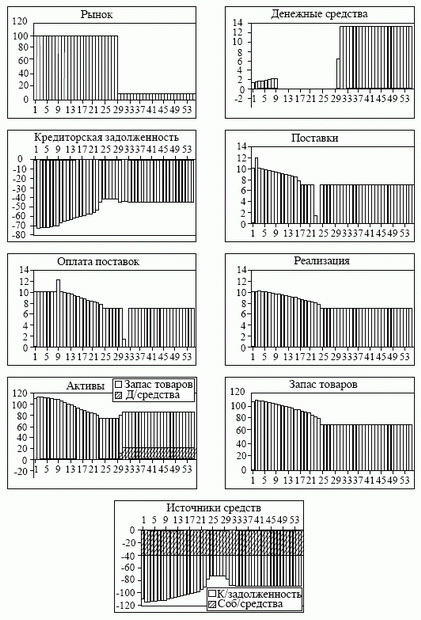
На рис. 5.9 представлено одно из таких решений, полученное при следующих параметрах и начальных условиях:
![\begin{array}{с}
t_0 = 1 \text{ нед.; } \\
t_{p1} = 56 \text{ нед.; } \\
r(t) = \left \{
\begin{array}{ll}
20 \text{ тыс.руб./нед.,} & \text{если } t \le 30 \text{ нед.} \\
7 \text{ тыс.руб./нед.,} & \text{если } t > 30 \text{ нед.}
\end{array};\\
Z(t_0) = 110 \text{ тыс.руб.; } \\
D(t_0) = 1,1 \text{ тыс.руб.; } \\
K(t_0) = -70 \text{ тыс.руб.; } \\
f_{pros}(t_0) = f_{pos}(t_0) = 10 \text{ тыс.руб./нед.; } \\
f_{op1}(t)|_{t \in [t_0,t_0 + T_к]} = 10 \text{ тыс.руб./нед.; } \\
T_z = 11 \text{ нед.; } \\
T_к = 7 \text{ нед.; } \\
S_{уст} = 41,1 \text{ тыс.руб.}
\end{array}](/sites/default/files/tex_cache/4c05623d27b1c285820b9939e96af8b0.png)
Оптимальный план в этих условиях - это заблаговременное и достаточно плавное снижение продаж, поставок и запаса товаров до постоянного пониженного уровня к моменту 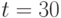 нед. Существенное снижение наблюдается около 8-й недели, так что период
"подготовки" к падению рынка составляет приблизительно удвоенный период оборачиваемости запаса товаров.
нед. Существенное снижение наблюдается около 8-й недели, так что период
"подготовки" к падению рынка составляет приблизительно удвоенный период оборачиваемости запаса товаров.
В конце этого периода реализуется ступенчатое управление поставками и продажами, напоминающее рассмотренное выше управление по типу "лестницы". Таким образом, подтверждается сделанное выше предположение о характере оптимального плана.
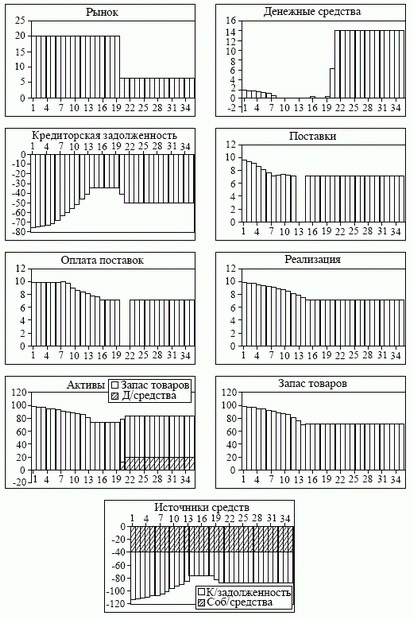
Единовременная поставка партии в начале периода планирования выглядит на графике как импульс на фоне плавного уменьшения поставок и не является погрешностью решения. В многочисленных экспериментах с компьютерной программой планирования установлено, что величина и наличие единовременной поставки зависит от величины денежных средств. С их ростом величина партии увеличивается, но поставка всегда остается единовременной. При уменьшении начальных денежных средств до некоторой величины, меньшей единицы процентов от запаса товаров, единовременная поставка партии не планируется (рис. 5.10), а при дальнейшем уменьшении получить решение задачи не удается.
увеличить изображение
Рис. 5.10. Численное решение задачи планирования простейшего предприятия с пониженным начальным запасом денежных средств
Учитывая выполненный выше графоаналитический анализ, наличие единовременной поставки в оптимальном плане можно объяснить избыточностью начального запаса денежных средств, так что суммарные за период планирования продажи можно увеличить путем конвертации денег в запас товаров. Очевидно, быстрее всего и с большим приростом продаж это можно сделать путем "импульсной" поставки.
Величина партии автоматически подбирается оптимизатором так, чтобы полученный выигрыш в продажах не компенсировался более ранним началом снижения поставок и реализации, соответственно, бульшими потерями продаж на участке непосредственно перед падением рынка. Невозможность получить решение при слишком малом запасе денежных средств можно объяснить по аналогии с "лестничным" управлением. В таком случае на начальном участке искусственного уменьшения поставок и продаж возможно лишь незначительное снижение, что аналогично увеличению числа начальных ступеней "лестницы" и приводит к удлинению необходимого периода снижения. В результате длина отрезка времени от начального момента до падения рынка оказывается недостаточной для реализации управления.
На участке пониженного рынка, в случае, если изображающая точка находится ниже точки 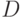 (
рис. 5.5, в), существует неопределенность в части возможной конвертации запаса денежных средств в запас товаров, поскольку такая конвертация не влияет на интенсивность потока продаж.
(
рис. 5.5, в), существует неопределенность в части возможной конвертации запаса денежных средств в запас товаров, поскольку такая конвертация не влияет на интенсивность потока продаж.
Изображающая точка может находиться в любой точке на горизонтальной линии между крайним левым и крайним правым положением. Поэтому для этого участка могут наблюдаться различные решения задачи, изменяющиеся от одной процедуры оптимизации к другой. Для снятия неопределенности задача решалась при дополнительном ограничении, требующем значения коэффициента абсолютной ликвидности не менее минимально достижимого на участке падения рынка. Это означает требование нахождения изображающей точки в крайнем левом положении, обеспечение максимально возможного запаса денежных средств и создание высоколиквидного "буфера" на непредвиденный случай.
Выполненное исследование задачи планирования простейшего предприятия позволяет сделать ряд заключений в отношении некоторых причин возможного снижения эффективности функционирования и охарактеризовать планирование в этих условиях.
Вопрос о соответствии финансирования и потребности в нем в условиях товарного кредита поставщиков решается графоаналитическим методом с помощью диаграммы (см. рис. 5.5, в). Диаграмма позволяет рассчитать максимальную интенсивность потока продаж, которая достижима при финансировании собственными средствами и товарным кредитом с постоянным периодом отсрочки оплаты поставок.
Если позволяет рынок, эта интенсивность обеспечивает максимум продаж и рентабельности собственных средств, бульшую, чем в отсутствие поставок в кредит. Однако в этих условиях необходимо планировать продажи несколько заниженные по сравнению с максимально достижимыми, что обеспечит снижение риска неплатежеспособности при возможном снижении спроса.
Если в качестве ограничений продаж выступает рыночный спрос, диаграмма позволяет выяснить избыточность финансирования и возможные пределы конвертации избыточного запаса товаров в запас денежных средств без снижения рентабельности. С точки зрения минимизации рисков в этом случае желательно иметь бульший запас денежных средств.
Резкие изменения рыночного спроса (которые в рамках задачи планирования рассматриваются как предсказуемые) приводят к существенно различным последствиям как в части рисков, так и в отношении планирования.
Случай, когда рыночные ограничения продаж изменяются с уровня, меньшего, чем позволяет финансирование, на больший, можно назвать благоприятным. И переход следует планировать в виде единовременной поставки партии в момент увеличения непрерывной интенсивности потока поставок, что обеспечивает максимальную рентабельность.
Случай уменьшения рыночных продаж до уровня, меньшего чем позволяет финансирование, содержит потенциальную опасность ситуации неплатежеспособности и требует плавного перехода продаж и поставок к пониженному уровню.
Оптимальные по рентабельности планы перехода могут быть построены с помощью разработанного метода моделирования и оптимизации.
Процессы, возникающие при этих переходах в системе внутрипроизводственных потоков, можно назвать переходными. При этом модель простейшего предприятия безынерционна при необходимости увеличения продаж и проявляет определенную инерцию при их снижении.