| Азербайджан |
Нелинейный классификатор. Многослойный персептрон
5.4.2.1 Алгоритм обратной волны. Суть – аппроксимация непрерывной дифференцируемой функцией за счет замены функции активации "сигмовидной" функцией:
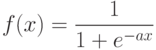
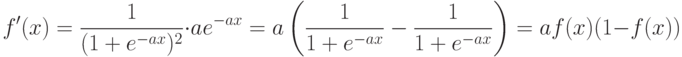

5.4.2.2. Метод градиентного спуска решения задачи минимизации.
Пусть 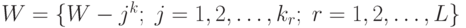 .
Тогда метод градиентного спуска выглядит так:
.
Тогда метод градиентного спуска выглядит так:

 а – шаг градиентного спуска. Очевидно, для его
реализации необходимо уметь вычислять градиент
а – шаг градиентного спуска. Очевидно, для его
реализации необходимо уметь вычислять градиент  .
.5.4.2.3. Вычисление градиента. Аргумент функции активации  -ого
нейрона
-ого
нейрона  -ого слоя
-ого слоя
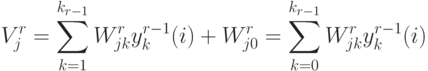
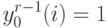 .
.Во входном слое, при  .
В выходном слое, при
.
В выходном слое, при 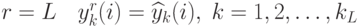 .
.
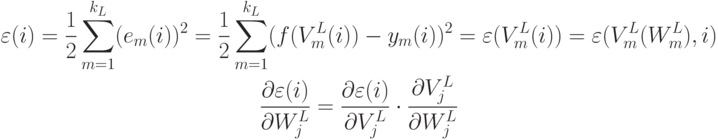
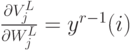 – не зависит от
– не зависит от  -ого
номера нейрона в слое, т.е. имеем одинаковый вектор производных для всех нейронов
-ого
номера нейрона в слое, т.е. имеем одинаковый вектор производных для всех нейронов 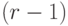 -ого слоя.
-ого слоя.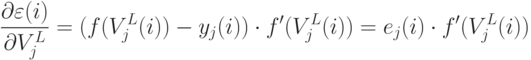
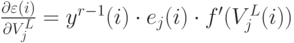
Рассмотрим скрытый слой 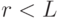 . Имеется зависимость:
. Имеется зависимость:
![\begin{gathered}
V_k^r=V_k^r(V_j^{r-1}) \\
\frac{\partial\varepsilon(i)}{\partial V_j^{r-1}(i)}=\sum_{k-1}^{k_r}
\frac{\partial\varepsilon(i)}{\partial V_k^r(i)}\cdot
\frac{\partial V_k^r(i)}{\partial V_j^{r-1}(i)} \\
\frac{\partial V_k^r(i)}{\partial V_j^{r-1}(i)}=
\frac{\partial}{\partial V_j^{r-1}(i)}
\left[\sum_{m=0}^{k_{r-1}}W_{km}^r y_m^{r-1}(i)\right],
\end{gathered}](/sites/default/files/tex_cache/247a62903b3c2a287f5b967f7d009809.png)
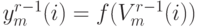 , следовательно:
, следовательно:![\begin{gathered}
\frac{\partial V_k^r(i)}{\partial V_j^{r-1}(i)}=W_{kj}^r
\frac{\partial y_j^{r-1}(i)}{\partial V_j^{r-1}(i)}=
W_{kj}^r f'(V_j^{r-1}(i)) \\
\frac{\partial\varepsilon(i)}{\partial V_j^{r-1}(i)}=
\left[\sum_{k-1}^{k_r}\frac{\partial\varepsilon(i)}{\partial V_k^r(i)}W_{kj}^r\right]
\cdot f'(V_j^{r-1}(i))
\end{gathered}](/sites/default/files/tex_cache/5c971085b92c19ead2490d347506173c.png)
5.4.2.4. Описание алгоритма.
0. Начальное приближение. Случайно выбираются веса небольших значений: 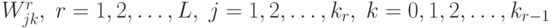 .
.
1. Прямой проход. Для каждого вектора прецедента 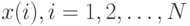 ,
вычисляются все
,
вычисляются все 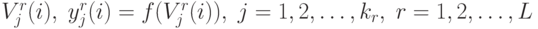 .
Вычисляется текущее значение ценовой функции
.
Вычисляется текущее значение ценовой функции  :
:
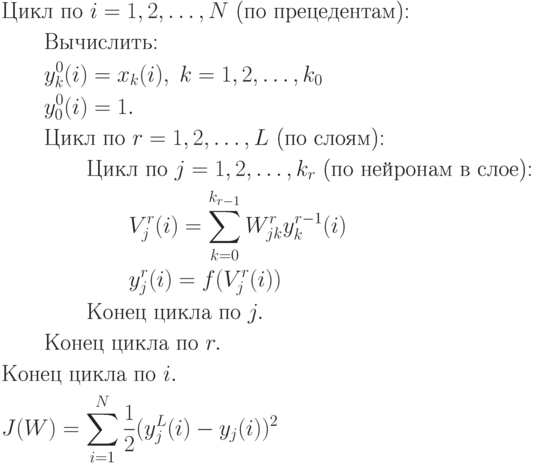
2. Обратный проход. Для каждого значения 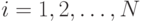 и
и 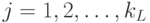 вычисляется
вычисляется 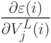 .
Затем последовательно необходимо вычислить
.
Затем последовательно необходимо вычислить 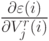 для всех
для всех  и
и 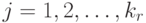 :
:
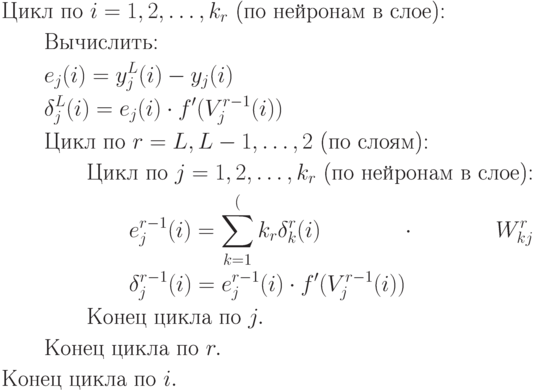
3. Пересчет весов.
Для всех 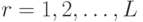 и
и  ,
где
,
где  .
.
- Останов алгоритма может происходить по двум критериям: либо
 стала меньше порога, либо градиент стал очень мал.
стала меньше порога, либо градиент стал очень мал. - От выбора
 зависит скорость сходимости. Если
зависит скорость сходимости. Если  мало, то скорость сходимости также мала. Если
мало, то скорость сходимости также мала. Если  велико, то и скорость сходимости высока, но при такой скорости можно пропустить
велико, то и скорость сходимости высока, но при такой скорости можно пропустить  .
. - В силу многоэкстремальности существует возможность спустить в локальный минимум. Если данный минимум по каким-то причинам не подходит, надо начинать алгоритм с другой случайной точки.
- Данный алгоритм быстрее, чем алгоритм с обучением.

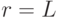 .
.