| Азербайджан |
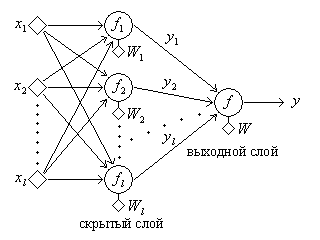
Нелинейный классификатор. Многослойный персептрон
5.2. Классификационные способности двухслойного персептрона
Рассмотрим общий случай двухслойного персептрона. Пусть  и в
скрытом слое
и в
скрытом слое  нейронов. Скрытый слой нейронов отображает
нейронов. Скрытый слой нейронов отображает 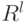 в
в  , где
, где ![H_p=\{(y_1,y_2,\ldots,y_p)\in R_p,\; y_i\in[0,1],\;1\leq i\leq p\}](/sites/default/files/tex_cache/55764e1c41ce9c63c0912d4dbc117b2e.png) – гиперкуб. Другими словами, каждый нейрон задает гиперплоскость,
которая разделяет пространство пополам, т.е. скрытый слой нейронов
делит пространство
– гиперкуб. Другими словами, каждый нейрон задает гиперплоскость,
которая разделяет пространство пополам, т.е. скрытый слой нейронов
делит пространство 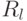 на полиэдры. Все вектора из каждого полиэдра
отображаются в вершину
на полиэдры. Все вектора из каждого полиэдра
отображаются в вершину  -мерного единичного куба. Выходной нейрон
разделяет вектора в классах, описанных полиэдрами, т.е. производит
сечение гиперкуба, полученного в скрытом слое.
-мерного единичного куба. Выходной нейрон
разделяет вектора в классах, описанных полиэдрами, т.е. производит
сечение гиперкуба, полученного в скрытом слое.
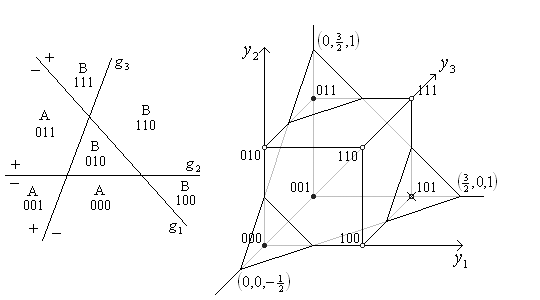
Пример. Рассмотрим нейронную сеть с двумя входами  и тремя
нейронами
и тремя
нейронами  . Тогда пространство
. Тогда пространство  . Пусть первый слой нейронов задает
разбиение признакового пространства (плоскости) как показано на
рисунке. В каждом многоугольнике (возможно, бесконечном) все точки
соответствуют одному классу (A или B). При этом в каждом
многоугольнике знаки линейных функционалов
. Пусть первый слой нейронов задает
разбиение признакового пространства (плоскости) как показано на
рисунке. В каждом многоугольнике (возможно, бесконечном) все точки
соответствуют одному классу (A или B). При этом в каждом
многоугольнике знаки линейных функционалов 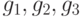 остаются
постоянными. Следовательно, с каждым многоугольником связано
определенное значение вектора выходов нейронов первого слоя, причем
для разных многоугольников эти значения различны. Поскольку значениями
компонент этого вектора являются 0 либо 1, получаем, что каждому
многоугольнику соответствует некоторая вершина единичного куба
остаются
постоянными. Следовательно, с каждым многоугольником связано
определенное значение вектора выходов нейронов первого слоя, причем
для разных многоугольников эти значения различны. Поскольку значениями
компонент этого вектора являются 0 либо 1, получаем, что каждому
многоугольнику соответствует некоторая вершина единичного куба  в
пространстве
в
пространстве 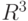 . При этом каждой вершине куба сопоставлен один класс A
или B. На рисунке изображен единичный куб
. При этом каждой вершине куба сопоставлен один класс A
или B. На рисунке изображен единичный куб  , у которого закрашенные
вершины относятся к классу
, у которого закрашенные
вершины относятся к классу  , а не закрашенные – к классу
, а не закрашенные – к классу  . Задача
нейрона второго слоя состоит в разделении вершин этого куба. Нетрудно
видеть, что в нашем примере плоскость
. Задача
нейрона второго слоя состоит в разделении вершин этого куба. Нетрудно
видеть, что в нашем примере плоскость  является разделяющей для куба
является разделяющей для куба  .
Она и задает параметры нейрона второго слоя. Заметим, что вершина
.
Она и задает параметры нейрона второго слоя. Заметим, что вершина 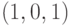 в кубе не загружена, т.е. в нее не отображается ни один
многоугольник.
в кубе не загружена, т.е. в нее не отображается ни один
многоугольник.
5.3. Трехслойный персептрон
Внешний (выходной) нейрон реализует лишь одну гиперплоскость. Очевидно, что одна разделяющая гиперплоскость не всегда может обеспечить желаемое разделение вершин гиперкуба. Например, если два конца одной его главной диагонали относятся к классу A, а два конца другой диагонали – к классу B. С аналогичной ситуацией мы уже сталкивались в задаче исключающего или. Попробуем ввести еще один слой нейронов.
Утверждение. Трехслойная нейронная сеть позволяет описать любые разделения объединений полиэдров.
Доказательство. Рассмотрим первый слой из  нейронов. На
первом формируются гиперплоскости, т.к. строится полиэдральное
разбиение пространства гиперплоскостями. Очевидно, что для заданного
конечного множества прецедентов всегда можно построить разбиение
пространства признаков на полиэдры такое, что ни в каком полиэдре не
окажется пары точек из разных классов. Как было показано выше, первый
слой отображает полиэдры в вершины
нейронов. На
первом формируются гиперплоскости, т.к. строится полиэдральное
разбиение пространства гиперплоскостями. Очевидно, что для заданного
конечного множества прецедентов всегда можно построить разбиение
пространства признаков на полиэдры такое, что ни в каком полиэдре не
окажется пары точек из разных классов. Как было показано выше, первый
слой отображает полиэдры в вершины  -мерного единичного гиперкуба.
Поскольку с каждым полиэдром связаны образы одного класса, то и с
каждой вершиной гиперкуба связан лишь один класс.
-мерного единичного гиперкуба.
Поскольку с каждым полиэдром связаны образы одного класса, то и с
каждой вершиной гиперкуба связан лишь один класс.
Каждый нейрон второго слоя описывает сечение полученного
гиперкуба. Выберем в качестве таких сечений гиперплоскости, отсекающие
ровно одну вершину гиперкуба. Поскольку число вершин в гиперкубе равно 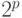 , число нейронов второго слоя также равно
, число нейронов второго слоя также равно 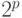 . Таким образом, выход
нейронов второго слоя имеет следующий вид. Это вектор размерности
. Таким образом, выход
нейронов второго слоя имеет следующий вид. Это вектор размерности 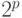 ,
у которого всегда лишь одно значение равно 1, а остальные равны нулю.
Назовем нейроны второго слоя нейронами класса A или B в соответствии с
классом вершины гиперкуба, которую отсекает этот нейрон. Теперь
становится понятно, каким образом строить третий слой нейронной сети.
Нужно в выходном нейроне третьего слоя реализовать оператор
логического сложения выходов нейронов второго слоя, относящихся к
классу A. Таким образом разделяющая гиперплоскость выходного нейрона
задается уравнением:
,
у которого всегда лишь одно значение равно 1, а остальные равны нулю.
Назовем нейроны второго слоя нейронами класса A или B в соответствии с
классом вершины гиперкуба, которую отсекает этот нейрон. Теперь
становится понятно, каким образом строить третий слой нейронной сети.
Нужно в выходном нейроне третьего слоя реализовать оператор
логического сложения выходов нейронов второго слоя, относящихся к
классу A. Таким образом разделяющая гиперплоскость выходного нейрона
задается уравнением:
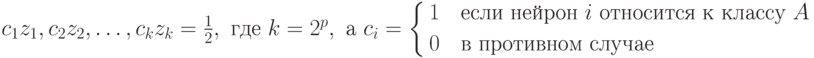
Таким образом, можно построить трехслойный персептрон следующим образом. Нейроны первого слоя разделяют пространство признаков на полиэдры одного класса и отображают их в вершины гиперкуба. Нейроны второго слоя отсекают вершины гиперкуба. Нейрон третьего слоя собственно осуществляет классификацию через оператор логического сложения. Тем самым утверждение доказано.
Рассмотрим, как строится уравнение гиперплоскости, отсекающей
вершину  -мерного единичного гиперкуба. Диагональ куба имеет длину
-мерного единичного гиперкуба. Диагональ куба имеет длину 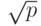 .
Длины диагоналей
.
Длины диагоналей  -мерных единичных гиперкубов, являющихся боковыми
гранями
-мерных единичных гиперкубов, являющихся боковыми
гранями  -мерного куба, равны
-мерного куба, равны  .
Центр куба находится в точке
.
Центр куба находится в точке  .
Расстояние от центра куба до любой вершины равно
.
Расстояние от центра куба до любой вершины равно  . Плоскость проводим
перпендикулярно главной диагонали куба, инцидентной вершине, которую
надо отсечь, так, чтобы расстояние от этой вершины до секущей
плоскости было равно
. Плоскость проводим
перпендикулярно главной диагонали куба, инцидентной вершине, которую
надо отсечь, так, чтобы расстояние от этой вершины до секущей
плоскости было равно  , причем данная точка должна находиться на
диагонали куба, проведенной к отсекаемой вершине.
, причем данная точка должна находиться на
диагонали куба, проведенной к отсекаемой вершине.
Пусть  – отделяемая вершина,
– отделяемая вершина,  – диагонально противоположная
вершина (
– диагонально противоположная
вершина (  , где
, где  обозначает
обозначает  -мерный вектор, состоящий из единиц).
Следовательно,
-мерный вектор, состоящий из единиц).
Следовательно,  – направляющий вектор разделяющей гиперплоскости.
Тогда гиперплоскость проходит через точку:
– направляющий вектор разделяющей гиперплоскости.
Тогда гиперплоскость проходит через точку:

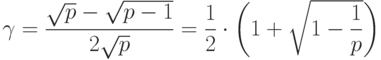

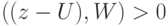 .
.