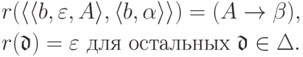|
Упражнение 2.1.25 |
Синтаксический разбор
Определение 13.1.22. Сентенциальной формой (sentential form)
грамматики  называется любое слово в алфавите
называется любое слово в алфавите  ,
выводимое из начального символа S.
,
выводимое из начального символа S.
Пример 13.1.23. Слова S, aSeaceSbb, aceaacecbecbb являются сентенциальными формами грамматики из примера 13.1.3.
Определение 13.1.24.
Пусть дана
контекстно-свободная грамматика  .
Определим три функции
.
Определим три функции  ,
, 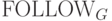 и
и 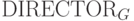 ,
связанные с грамматикой G.
Для краткости будем писать просто FIRST, FOLLOW и DIRECTOR.
,
связанные с грамматикой G.
Для краткости будем писать просто FIRST, FOLLOW и DIRECTOR.
Функция FIRST
ставит
в соответствие
каждому слову 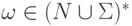 множество тех терминальных символов,
с которых начинаются слова,
выводимые из
множество тех терминальных символов,
с которых начинаются слова,
выводимые из 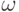 ,
то есть
,
то есть

Функция FOLLOW ставит в соответствие каждому нетерминальному символу A множество тех терминальных символов, которые могут встречаться в сентенциальных формах непосредственно справа от A, то есть
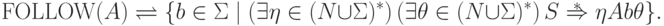
Функция DIRECTOR
ставит
в соответствие
каждому правилу 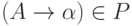 множество терминальных символов,
определяемое следующим образом:
если
множество терминальных символов,
определяемое следующим образом:
если  ,
то
,
то
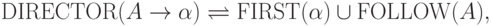
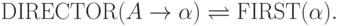
Пример 13.1.25. Рассмотрим контекстно-свободную грамматику из примера 13.1.3. Очевидно, что
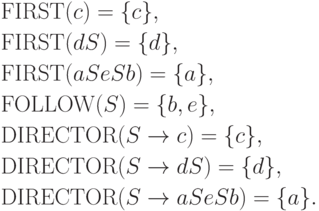
Пример 13.1.26.
Рассмотрим контекстно-свободную
грамматику  из примера 13.1.17.
Очевидно, что
из примера 13.1.17.
Очевидно, что
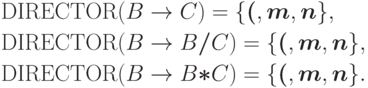
Пример 13.1.27. Пусть контекстно-свободная грамматика 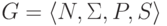 не содержит бесполезных символов.
Пусть даны
правило
не содержит бесполезных символов.
Пусть даны
правило 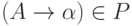 и
символ
и
символ 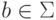 . Тогда утверждение
. Тогда утверждение

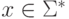 ,
,  и
и 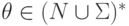 , что
, что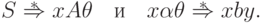
Теорема 13.1.28. Пусть дана
контекстно-свободная грамматика  . Пусть
. Пусть 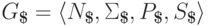 - соответствующая
контекстно-свободная
грамматика с маркером конца строки,
приведенная в определении 13.1.16. Обозначим через M МП-автомат
- соответствующая
контекстно-свободная
грамматика с маркером конца строки,
приведенная в определении 13.1.16. Обозначим через M МП-автомат  , где
, где
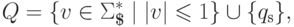
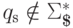 ,
, 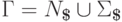 и
и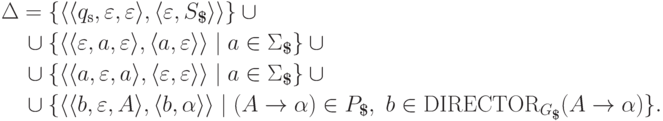
Доказательство.
Индукцией по количеству тактов
можно доказать, что
если 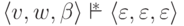 ,
где
,
где  ,
то
,
то ![\smash[b]{ \beta \overstar{\myunderset{ G_\eos }{\Rightarrow }} v w }](/sites/default/files/tex_cache/622e89660a80451740ad154f11c52286.png) .
Следовательно,
.
Следовательно, 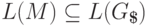 .
.
С другой стороны,
докажем, что если
в грамматике  выводится
выводится  и
и 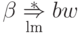 ,
где
,
где  ,
, 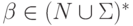 ,
, 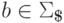 ,
,  ,
то
,
то 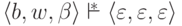 .
.
Проведем доказательство индукцией по сумме
длины слова bw
и длины вывода 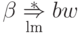 .
Случай |bw| = 1,
.
Случай |bw| = 1, 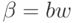 образует базис индукции
(очевидно,
что
образует базис индукции
(очевидно,
что 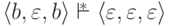 ).
Проверим теперь шаг индукции.
Так как
).
Проверим теперь шаг индукции.
Так как  и
и  ,
то
,
то 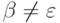 .
Если
.
Если 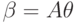 ,
где
,
где 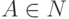 ,
то вывод
,
то вывод 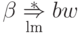 имеет вид
имеет вид
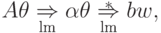
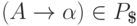 и в силу леммы 13.1.27
и в силу леммы 13.1.27  .
Отсюда получаем, что
.
Отсюда получаем, что 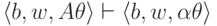 ,
и остается применить предположение индукции для левосторонних выводов
,
и остается применить предположение индукции для левосторонних выводов  и
и  .
Если же
.
Если же 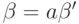 ,
где
,
где  ,
то, очевидно, a = b
и
,
то, очевидно, a = b
и  .
Если
.
Если 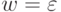 ,
то
,
то 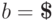 и в силу леммы 13.1.19
и в силу леммы 13.1.19  ,
но этот случай уже рассмотрен в базисе индукции.
Пусть
,
но этот случай уже рассмотрен в базисе индукции.
Пусть 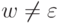 .
Тогда w = b'w'
для некоторых
.
Тогда w = b'w'
для некоторых 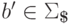 и
и  .
Обозначим u' = ub.
Применяя предположение индукции для левосторонних выводов
.
Обозначим u' = ub.
Применяя предположение индукции для левосторонних выводов  и
и 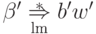 ,
получаем
,
получаем 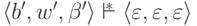 .
Согласно построению МП-автомата M
имеем
.
Согласно построению МП-автомата M
имеем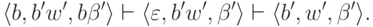
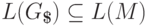 .
.Гомоморфизм 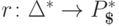 задается соотношениями
задается соотношениями