|
Упражнение 2.1.25 |
Автоматы с магазинной памятью
10.3*. Автоматы с магазинной памятью с однобуквенными переходами
Теорема 10.3.1. Каждый МП-автомат эквивалентен некоторому МП-автомату 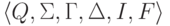 , где |Q| = 2 и каждый переход
, где |Q| = 2 и каждый переход 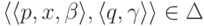 удовлетворяет требованиям |x| = 1,
удовлетворяет требованиям |x| = 1,  и
и  .
.
Доказательство.
Пусть исходным МП-автоматом распознается
контекстно-свободный
язык  .
Согласно теореме 8.4.6
язык
.
Согласно теореме 8.4.6
язык 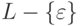 порождается некоторой
контекстно-свободной грамматикой
порождается некоторой
контекстно-свободной грамматикой  ,
в которой каждое правило имеет вид
,
в которой каждое правило имеет вид 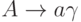 ,
где
,
где 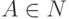 ,
, 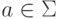 ,
, 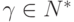 и
и  .
Аналогично тому, как было сделано при доказательстве
теоремы 10.2.1,
положим
.
Аналогично тому, как было сделано при доказательстве
теоремы 10.2.1,
положим 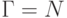 , Q = {1,2}, I = {1},
, Q = {1,2}, I = {1},

Теорема 10.3.2. Каждый МП-автомат эквивалентен некоторому МП-автомату 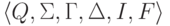 , в котором каждый переход
, в котором каждый переход 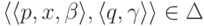 удовлетворяет требованиям |x| = 1,
удовлетворяет требованиям |x| = 1,  и
и  .
.
Доказательство.
Пусть исходным МП-автоматом распознается
контекстно-вободный язык  .
Согласно теореме 8.4.6
язык
.
Согласно теореме 8.4.6
язык 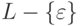 порождается некоторой
контекстно-вободной грамматикой
порождается некоторой
контекстно-вободной грамматикой 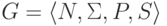 ,
в которой
каждое правило имеет один из следующих трех видов:
,
в которой
каждое правило имеет один из следующих трех видов: 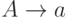 ,
,  ,
, 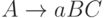 ,
где
,
где 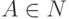 ,
, 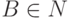 ,
, 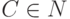 ,
, 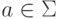 .
Легко добиться того, чтобы
в правилах грамматики G
вспомогательные символы в правой части
(то есть символы B и C )
были отличны от начального символа S.
.
Легко добиться того, чтобы
в правилах грамматики G
вспомогательные символы в правой части
(то есть символы B и C )
были отличны от начального символа S.
Положим 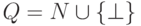 ,
где
,
где 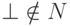 .
Далее, положим
.
Далее, положим 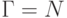 ,
,
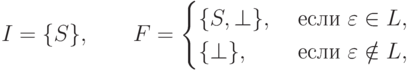
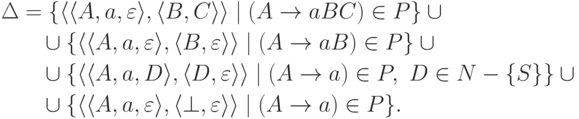
Упражнение 10.3.3. Найти для языка, порождаемого грамматикой
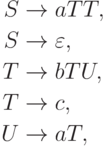
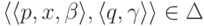 удовлетворяет требованиям |x| = 1,
удовлетворяет требованиям |x| = 1,  и
и  .
.Упражнение 10.3.4. Найти для языка, порождаемого грамматикой
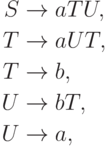
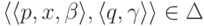 удовлетворяет требованиям
удовлетворяет требованиям  ,
,  и
и  .
.