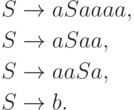НОУ ИНТУИТ | Математическая теория формальных языков. Лекция 8: Неоднозначность в контекстно-свободных грамматиках

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 09.07.2007 | Уровень: профессионал | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 33 студентам

| Поделиться |

Поддержать программу

7.2. Однозначные контекстно-свободные грамматики

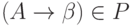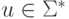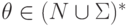Определение 7.2.1. Вывод в контекстно-свободной грамматике называется левосторонним ( левым, leftmost derivation), если на каждом шаге вывода заменяется самое левое из всех вхождений вспомогательных символов (то есть каждый шаг вывода имеет вид $u A \theta \Rightarrow u \beta \theta$ , где $( A \tto \beta ) \in P$ , $u \in \Sigma ^*$ и $\theta \in \ns ^*$ ). Иногда в левосторонних выводах вместо $\Rightarrow$ пишут \lmarrow. Правосторонний ( правый ) вывод определяется аналогично. В правосторонних выводах вместо $\Rightarrow$ пишут \rmarrow.

Пример 7.2.2. Вывод

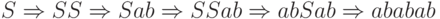
$S \Rightarrow SS \Rightarrow Sab \Rightarrow SSab \Rightarrow abSab \Rightarrow ababab$

из примера 7.1.2 не является левосторонним.

Лемма 7.2.3. Для каждого слова, выводимого в контекстно-свободной грамматике, существует левосторонний вывод.

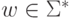Лемма 7.2.4. Пусть G - контекстно-свободная грамматика над алфавитом $\Sigma$ . Пусть $w \in \Sigma ^*$ . Тогда существует взаимно-однозначное соответствие между левосторонними выводами слова w в грамматике G и деревьями вывода в грамматике G, кроной которых является w.

Пример 7.2.5. Рассмотрим дерево вывода из примера 7.1.2. Ему соответствует левосторонний вывод

$S \mymathrel{\lmarrow} SS \mymathrel{\lmarrow} SSS \mymathrel{\lmarrow} abSS \mymathrel{\lmarrow} ababS \mymathrel{\lmarrow} ababab .$

Определение 7.2.6. Контекстно-свободная грамматика называется неоднозначной (ambiguous), если существует слово, которое имеет два или более левосторонних вывода (устаревший термин - неопределенная грамматика). В противном случае контекстно-свободная грамматика называется однозначной (unambiguous).

Пример 7.2.7. Контекстно-свободная грамматика из примера 7.1.2 неоднозначна. Слово ababab имеет два левосторонних вывода:

$S \mymathrel{\lmarrow} SS \mymathrel{\lmarrow} SSS \mymathrel{\lmarrow} abSS \mymathrel{\lmarrow} ababS \mymathrel{\lmarrow} ababab$

и

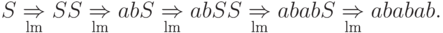
$S \mymathrel{\lmarrow} SS \mymathrel{\lmarrow} abS \mymathrel{\lmarrow} abSS \mymathrel{\lmarrow} ababS \mymathrel{\lmarrow} ababab .$

Пример 7.2.8. Пусть $\Sigma = \{ \trm{p} , \trm{\#} , \trm{)} , \trm{(} , \trm{\lnot} , \trm{\land} , \trm{\lor} \}$ . Контекстно-свободная грамматика

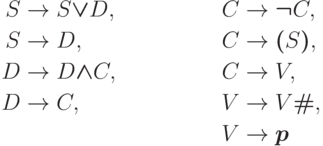
$\begin{align*} S \; & {\to} \; S \trm{\lor} D , & C \; & {\to} \; \trm{\lnot} C , \\ S \; & {\to} \; D , & C \; & {\to} \; \trm{(} S \trm{)} , \\ D \; & {\to} \; D \trm{\land} C ,& C \; & {\to} \; V , \\ D \; & {\to} \; C , & V \; & {\to} \; V \trm{\#} , \\ & & V \; & {\to} \; \trm{p} \end{align*}$

порождает множество всех булевых формул, составленных из переменных p, p#, p##, ..., с помощью скобок и операторов $\trm{\lnot}$ , $\trm{\land}$ и $\trm{\lor}$ . Эта грамматика является однозначной.

Определение 7.2.9. Контекстно-свободный язык называется существенно неоднозначным (inherently ambiguous), если каждая контекстно-свободная грамматика, порождающая этот язык, является неоднозначной.

Пример 7.2.10. Язык, порождаемый контекстно-свободной грамматикой из примера 7.1.2, не является существенно неоднозначным. Он порождается однозначной грамматикой

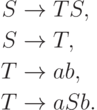
$\begin{align*} S \; & {\to} \; TS , \\ S \; & {\to} \; T , \\ T \; & {\to} \; ab , \\ T \; & {\to} \; aSb . \end{align*}$

Пример 7.2.11. Пусть 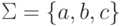$\Sigma = \{ a , b , c \}$ . Контекстно-свободный язык {a^kb^mcⁿ | k = m или m = n} является существенно неоднозначным. Доказательство этого факта можно найти в [АхоУль, с. 234-236].

Упражнение 7.2.12. Однозначна ли контекстно-свободная грамматика

$\begin{align*} K \; & {\to} \; a , \\ K \; & {\to} \; b , \\ K \; & {\to} \; K \trm{+} K ,\\ K \; & {\to} \; K \trm{-} K \end{align*}$

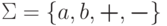с алфавитом $\Sigma = \{a,b,\trm{+},\trm{-}\}$ ?

Упражнение 7.2.13. Однозначна ли контекстно-свободная грамматика

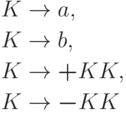
$\begin{align*} K \; & {\to} \; a , \\ K \; & {\to} \; b , \\ K \; & {\to} \; \trm{+} K K , \\ K \; & {\to} \; \trm{-} K K \end{align*}$

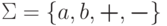с алфавитом $\Sigma = \{a,b,\trm{+},\trm{-}\}$ ?

Упражнение 7.2.14. Однозначна ли контекстно-свободная грамматика

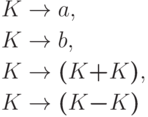
$\begin{align*} K \; & {\to} \; a , \\ K \; & {\to} \; b , \\ K \; & {\to} \; \trm{(} K \trm{+} K \trm{)} , \\ K \; & {\to} \; \trm{(} K \trm{-} K \trm{)} \end{align*}$

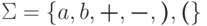с алфавитом $\Sigma = \{a,b,\trm{+},\trm{-},\trm{)},\trm{(}\}$ ?

Упражнение 7.2.15. Однозначна ли контекстно-свободная грамматика

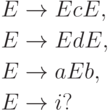
$\begin{align*} E \; & {\to} \; E c E , \\ E \; & {\to} \; E d E , \\ E \; & {\to} \; a E b , \\ E \; & {\to} \; i ? \end{align*}$

Упражнение 7.2.16.Найти однозначную контекстно-свободную грамматику, эквивалентную грамматике

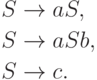
$\begin{align*} S \; & {\to} \; a S , \\ S \; & {\to} \; a S b , \\ S \; & {\to} \; c . \end{align*}$

Упражнение 7.2.17.Найти однозначную контекстно-свободную грамматику, эквивалентную грамматике

$\begin{align*} S \; & {\to} \; a S aaaa , \\ S \; & {\to} \; a S aa , \\ S \; & {\to} \; aa S a , \\ S \; & {\to} \; b . \end{align*}$

Дальше >>

Математическая теория формальных языков

Математическая теория формальных языков

Неоднозначность в контекстно-свободных грамматиках

7.2. Однозначные контекстно-свободные грамматики

Вопросы и ответы

Студенты

Авторизоваться

Математическая теория формальных языков

Математическая теория формальных языков

Неоднозначность в контекстно-свободных грамматиках

7.2. Однозначные контекстно-свободные грамматики

Вопросы и ответы

Студенты