|
Упражнение 2.1.25 |
Синтаксические моноиды
6.2. Минимизация детерминированных конечных автоматов
Определение 6.2.1.
Говорят, что слово w различает
состояния p
и q
полного детерминированного конечного автомата  ,
если одно из состояний
,
если одно из состояний  ,
,  заключительное, а другое не является заключительным.
заключительное, а другое не является заключительным.
Определение 6.2.2.
Состояния p
и q
полного детерминированного конечного автомата  называются различимыми
(distinguishable), если существует
слово w,
которое их различает.
называются различимыми
(distinguishable), если существует
слово w,
которое их различает.
Замечание 6.2.3.
Пусть полный детерминированный конечный автомат  задает язык L.
Рассмотрим произвольные слова
задает язык L.
Рассмотрим произвольные слова  и
и  .
Состояния
.
Состояния  и
и  различимы тогда и только тогда, когда
различимы тогда и только тогда, когда  .
.
Теорема 6.2.4. Существует быстрый алгоритм, позволяющий по произвольному детерминированному конечному автомату находить минимальный (по количеству состояний) автомат среди детерминированных конечных автоматов, эквивалентных исходному автомату.
Доказательство.
Без ограничения общности можно предположить,
что дан
полный детерминированный конечный автомат  ,
все состояния которого достижимы из начального состояния
(для обеспечения полноты достаточно добавить одно состояние).
Для каждого натурального числа i
определим на множестве Q
отношение эквивалентности
,
все состояния которого достижимы из начального состояния
(для обеспечения полноты достаточно добавить одно состояние).
Для каждого натурального числа i
определим на множестве Q
отношение эквивалентности  :
:
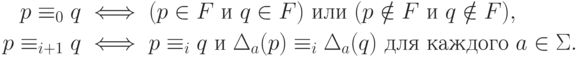
 тогда и только тогда, когда
никакое слово длины не больше i
не различает p и q.
Обозначим n =|Q|.
Легко проверить, что для любого
тогда и только тогда, когда
никакое слово длины не больше i
не различает p и q.
Обозначим n =|Q|.
Легко проверить, что для любого 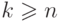 отношение
отношение  совпадает с отношением
совпадает с отношением  .
Используя классы эквивалентности
отношения
.
Используя классы эквивалентности
отношения  как состояния, можно построить минимальный
полный детерминированный конечный автомат.
Удалив из него бесполезное состояние
(из которого не достижимо ни одно заключительное состояние),
если такое имеется,
получим искомый минимальный
детерминированный конечный автомат.
как состояния, можно построить минимальный
полный детерминированный конечный автомат.
Удалив из него бесполезное состояние
(из которого не достижимо ни одно заключительное состояние),
если такое имеется,
получим искомый минимальный
детерминированный конечный автомат.Пример 6.2.5.
Рассмотрим полный детерминированный конечный автомат  ,
где
,
где

![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F=]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" ^{a}
\ar "2,2" ^{b}
& *=[o][F-]{2}
\ar "1,3" ^{b}
\ar "2,2" ^{a}
& *=[o][F=]{3}
\ar "1,4" ^{a}
\ar "2,2" ^{b}
& *=[o][F-]{4}
\ar `ul^l{+/u7mm/}`l^dl{[0,-3]}_{b} "1,1"
\ar "2,4" ^{a}
\\
%
& *=[o][F-]{6}
\rloop{0,-1} ^{a}
\rloop{-1,0} ^{b}
&
& *=[o][F-]{5}
\rloop{0,-1} ^{a}
\ar "2,2" ^{b}
}](/sites/default/files/tex_cache/b834e887114fc46fed116a76b729c24f.png)
 ,
где
,
где
![\objectwidth={7.5mm} \objectheight={7.5mm} \let\objectstyle=\scriptstyle
\xymatrix {
*=[o][F=]{1,3}
\ar @`{+/l16mm/} [] ^{}
\ar "1,2" <0.6mm> ^{a}
& *=[o][F-]{2,4}
\ar "1,1" <0.6mm> ^{b}
}](/sites/default/files/tex_cache/05dc1f06b2c61cce68fd7e29ff9faafe.png)
Замечание 6.2.6. Неизвестно, существует ли быстрый (полиномиальный) алгоритм, позволяющий по произвольному конечному автомату находить минимальный автомат среди всех (не обязательно детерминированных) конечных автоматов, эквивалентных исходному автомату.
Упражнение 6.2.7. Найти минимальный полный детерминированный конечный автомат для языка, порождаемого грамматикой

Упражнение 6.2.8. Найти минимальный полный детерминированный конечный автомат для языка
(1+(a+b)*b)b(a+b)*.
Упражнение 6.2.9. Найти минимальный полный детерминированный конечный автомат для языка
(a+b)*(aaba+(aabb+bbaa)abbb)(a+b)*.
Упражнение 6.2.10. Равны ли регулярные выражения
(aa+b+ab)* и ((a+b)*b+1)(aa)*?
Упражнение 6.2.11. Равны ли регулярные выражения
(a+b)*aa(a+b)*bb(a+b)* и (ab+b)*aa(a+b)*bb(a+ba)*?
Упражнение 6.2.12. Равны ли регулярные выражения
((ba+bb)(aa+ab)*)*a и b(aa+ab+ba+bb)*(aa+ba)?
Упражнение 6.2.13. Равны ли регулярные выражения
(ca+cb+cc+(a+b+(a+c))+c)(a+b+c)*
и
c(a+b+bc)++(a+b+c)*(ac+cc)(a+b+bc)*?

