Деление

Арифметические операции над числами, представленными с плавающей запятой

В основе арифметических операций над числами с плавающей запятой лежат принципы, на которых базируются операции над числами с фиксированной запятой. При этом есть и некоторые особенности.

Будем условно считать, что порядки заданы в обратном коде, а мантиссы – в прямом.

Умножение:

X = 2mx * sign X.x1x2...xn
Y = 2my * sign Y.y1y2...yn
Z = X*Y = 2mx+my * sign Z.z1z2...zn

Порядок выполнения операции следующий:

1. Знак произведения находится так же, как и при умножении чисел с фиксированной запятой:
2. Порядок произведения находится алгебраическим суммированием порядков мно­жимого и множителя.

3. Мантисса находится по правилам умножения чисел с фиксированной запятой.

   При этом возможны следующие случаи:

   • Мантисса произведения – ненормализованное число, так как

     

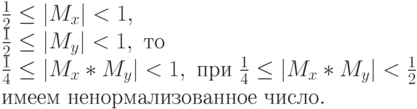
     Поэтому необходима нормализация влево максимум только на один разряд.

     С этой целью нужно сдвинуть мантиссу влево на один разряд. Это соответствует умножению числа на 2¹. Для того чтобы число не увеличилось в два раза, нужно из порядка вычесть единицу.

   • При умножении двух чисел в силу ограниченности разрядной сетки можно получить число, которое не может быть в ней представлено. Это соответствует получению машинной бесконечности.

     В данном случае вырабатывается специальный признак, по которому дальнейшие вычисления прекращаются.

   • При умножении двух чисел можно получить минимальное число, которое также не может быть представлено в разрядной сетке. Это соответствует случаю, когда получаемое число должно быть интерпретировано как нуль.

Деление

В основном аналогично умножению:

X = 2mx * sign X.x1x2...xn
Y = 2my * sign Y.y1y2...yn
Z = X/Y = 2mx–my * sign Z.z1z2...zn

Порядок выполнения операции следующий:

1. Находится по известным правилам знак частного.
2. Порядок частного находится как разность порядков делимого и делителя.

3. Цифры частного находятся так:

   вначале находится целая часть мантиссы, то есть

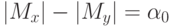
   Если , если 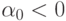, то z₀ = 0.

Дробная часть мантиссы находится так же, как при операциях над числами с фиксированной запятой. Такой порядок действий вытекает из того, что:

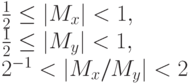
То есть, возможно получение ненормализованной мантиссы. Для нормализации мантиссу необходимо сдвинуть вправо на один разряд и, чтобы не уменьшать при этом результат в два раза, нужно прибавить к порядку одну единицу.

При делении, так же, как и при умножении, возможно получение кода машинного нуля и кода бесконечности.