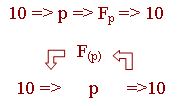Арифметические основы

Выбор системы счисления.

Возникает естественный вопрос, является ли общепринятая система счисления с основанием 10 оптимальной? Если да, то с каких позиций? Вопрос заслуживает внимания, т.к. одна из первых ВМ (ENIAC) использовала именно десятеричную систему.

Прямой и однозначный ответ на этот вопрос невозможен. Можно дать много различных ответов и все они будут справедливы лишь для каких-то определенных условий.

Введя общее представление числа в позиционной системе, мы усомнились в достоинствах десятеричной не потому, что она вдруг проявила свои отрицательные качества, а потому что ее преимущества явны лишь при ручных методах счета. Нас же интересуют, прежде всего, такие системы счисления, которые будут удобны и экономичны при автоматических вычислениях с помощью ЭВМ. Мы должны также помнить, что необходимо для этого иметь саму ЭВМ.

Покажем, что десятеричная система не устарела. Например, для производства экономичных расчетов обычно приходится иметь дело с очень большими объемами числовой информации. Тогда с введением новой системы пришлось бы воспользоваться следующей цепочкой действий:

Т.е. нужно было бы из десятеричной системы перевести информацию в " p "-систему, произвести над ней необходимые операции в системе " p ", затем снова сделать, но обратный перевод из " p "-системы в десятеричную, т.к. отказ от десятеричной системы потребовал бы и устранения первого этапа.

Если преобразование из десятеричной системы в " p "-систему требует не слишком много времени, в то же время, если выполнение функции F будет в системе " p " сделано много быстрее, то тогда эта цепочка действий будет оправданной.

Но для экономической информации характерно то, что очень несложные операции нужно производить всякий раз над большим объемом исходных данных. Так что в данном случае вряд ли целесообразно переходить к новой системе. Это и является объяснением того факта, что в настоящее время значительное число ЭВМ строится именно в десятеричной системе счисления.

Однако ЭВМ предназначены не только для выполнения экономических расчетов. В большинстве случаев неэкономических применений ЭВМ имеют дело с задачами, в которых общий объем исходных данных невелик, но общее число необходимых операций огромно. Именно для такого рода применений рассмотренная последовательность действий может оказаться выгодной.

Очевидно, что можно, не сужая области применения ЭВМ, задаться величиной некоторого самого большого числа. Пусть это будет число M. Воспользуемся позиционной системой счисления с основанием " p ", и тогда потребуется " n " разрядов, чтобы представить все M чисел:

Оборудование, которое нужно для хранения любого числа от 0 до M пропорционально произведению основания системы счисления на количество разрядов.

Таким образом, при заданном числе M количество цифроразрядов при основании " p ":

p*n = p* logpM,     (6.1)

где:

цифроразряд - эквивалент оборудования,

p*n - число устойчивых состояний элемента памяти,

n - число разрядов в числе.

Рассмотрим пример:

Пусть есть 24 цифроразряда.

1*1*...*12 = 409510
\________/
    12

2*2*...*23 = 656010
\________/
    8

3*3*...*34 = 409510
\________/
    6

5*5*5*56 = 129510
\______/
   4

7*7*78 = 51110
\____/
  3

Количество цифроразрядов говорит как о величине оборудования, так является характеристикой быстродействия. Как увидим позже, в позиционной системе счисления времена выполнения операций могут быть выражены через количество разрядов в числе.

Считаем " p " - величиной непрерывной. Находим производную от (6.1) по величине " p ". Берем вторую производную по " p ". Увидим, что первая производная обращается в нуль, а вторая - больше нуля при p = e. Т.е. получаем минимум при p = e.

Таким образом, оптимальной по оборудованию и быстродействию является система с основанием е.

Но е = 2,718...

Поэтому оптимальной является система с основанием р = 3.

Построим функцию, характеризующую отношение оборудования в системе с основанием " p " относительно системы с основанием " 2 ".

Т.е. 10-я система является более чем в 1,5 раза неэкономичной по отношению ко 2-ой системе, а 3-я система оказывается лишь на 5% экономичнее 2 й.

Действительное обоснование экономичности той или иной системы выглядит несколько сложнее.

Когда говорим об экономичности, то, прежде всего, имеем ввиду объем оборудования, сосредоточенный в АУ и ЗУ. Объем оборудования УУ не находится в столь простой зависимости от " p " да и в АУ учитывается лишь оборудование, связанное с элементами хранения информации, но не логическое оборудование.

Более детальный анализ показывает, что наиболее эффективными являются системы с основанием, кратным 2, т.е. 2, 4, 8, 16. Специфика построения схем ЭВМ показывает, что наиболее эффективной является 16-ая система. Именно она и применяется в современных машинах.

Мы же будем считать эффективной систему с основанием 2 по причине ее наибольшего распространения.

Вот основные соображения в пользу этой системы:

1. Высокая информационная эффективность.
2. Простота и надежность работы 2-ого элемента хранения информации (т.е. имеющего 2 устойчивых состояния)
3. Совпадение максимального числа состояний элемента с максимальным числом значений двоичной переменной, дающее возможность не строить специальные устройства для выполнения логических операций.
4. Простота построения схем для выполнения простых операций.
5. Более высокая скорость выполнения основных арифметических операций.

Последнее требует специального пояснения. В данном случае рассматриваются не отрезки времени, необходимые для выполнения тех или иных операций, а скорость, определяемая косвенно по относительному числу операций, которые требуется провести для выполнения, например, деления или умножения в двоичной или прочих системах.

Если " p " - основание системы счисления, то максимальная цифра в одном разряде - (p-1).

Если N - максимальное число, то для его изображения требуется log_pN разрядов.

Для того чтобы выполнить операцию умножения, например, потребуется (p-1)*log_pN операций сложения. Если сравнить это число операций в системе с основанием " p " и отнести его к числу операций в системе с основанием " 2 ", то может получиться следующая функция:

(p-1)*logpN        p-1
     ___________       _____
f(p)=              =          
       1*log2N         log2p

Это лишь основные соображения в пользу выбора в качестве основы двоичную систему счисления. Существуют и другие (контроль, диагностика неисправностей), но мы их из рассмотрения опустим.