Совершенные дизъюнктивные и конъюнктивные нормальные формы ФАЛ
Понятие функциональной полноты ФАЛ
Было отмечено, что техническая (физическая) задача синтеза произвольного устройства сводится к математической задаче построения произвольной ФАЛ.
Естественно возникает вопрос, какое количество связок необходимо, чтобы построить произвольную ФАЛ. Ответ на этот вопрос не однозначен. Мы видим, что, например, с помощью только функции f_{0} (константа 0 ), f_{15} (константа 1 ) произвольную ФАЛ построить нельзя. Нельзя ее построить и с помощью только инвертора. Существуют и другие базисы: 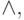
 1, |.
Есть также одноэлементные базисы: f_{8} – стрелка Пирса, f_{14} – штрих Шеффера, И-НЕ, ИЛИ-НЕ.
1, |.
Есть также одноэлементные базисы: f_{8} – стрелка Пирса, f_{14} – штрих Шеффера, И-НЕ, ИЛИ-НЕ.
Технически синтез устройства означает, что нужно иметь некоторый набор элементов, ФАЛ которых образуют базис, чтобы можно было построить реальное устройство.
Однако, как было отмечено, задача синтеза ФАЛ – идеальная модель. В действительности, для построения реальных устройств пользуются несколько более расширенным набором элементов - усиления и коррекции сигналов.
Минимизация ФАЛ и ограничения при ее рассмотрении
Покажем на примере, что СДНФ не является экономной формой записи:

на основании полного склеивания по Х_{2} мы видим, что запись стала короче, т.к. содержит меньшее число связок и букв. Физически это означает, что устройство, которое реализует эквивалентную, но более простую функцию, будет иметь в своем составе меньшее количество оборудования, а следовательно, будет работать надежнее.
Итак, задача синтеза устройства должна быть дополнена задачей уменьшения оборудования в нем. С математической точки зрения это задача построения минимальной ФАЛ.
Под минимальной ФАЛ понимается такая форма, в которой содержится меньшее количество букв и членов, чем в ее исходной форме.
Речь идет именно о буквах, а не о переменных, так в функции:
 имеется 6 букв и только 2 переменных.
имеется 6 букв и только 2 переменных.
Видно, что если какое-либо элементарное произведение входит в функцию, то при добавлении к нему новых сомножителей, полученное произведение так же будет входить в функцию.
Пример: если Х_{1}Х_{2} входит в функцию от любого числа аргументов ( >2 ), то в нее войдет, например, произведение Х_{1}Х_{2}Х_{3}.
Это можно показать так:

Дадим ряд определений:
- Произведение одной или нескольких неповторяющихся переменных, взятых с отрицанием или без него, называют элементарным.
Например, Х_{1} Х_{2} Х_{3} – элементарное произведение, т.к. в него входят различные буквы Х_{1} Х_{2} Х_{3}.
- Дизъюнкция элементарных произведений – ДНФ.
- ДНФ является минимальной, если в ней минимальное число букв и членов.
-
Конституентой единицы функции называют функцию, принимающую значение единицы только на одном наборе аргументов.
Обычно конституенты единицы выражают через произведение всех переменных, от которых зависит функция. СДНФ – дизъюнкция конституент единицы.
- Ранг произведения – число букв, входящих в него.
- Собственной частью называется произведение, полученное путем отбрасывания одной или нескольких переменных.
Например, Х_{1} Х_{2} Х_{3} Х_{4}, где Х_{1}, Х_{1} Х_{2}, Х_{1} Х_{2} Х_{3} – некоторые собственные части.
-
Если функция
 равна нулю на наборах аргументов, на которых обращается в нуль функция F, то говорят, что
равна нулю на наборах аргументов, на которых обращается в нуль функция F, то говорят, что  является импликантой функции F (т.е. нулей у импликанты не меньше, чем у функции).
является импликантой функции F (т.е. нулей у импликанты не меньше, чем у функции). - Простой импликантой называется произведение, которое само входит в выражение функции, но никакая его собственная часть в выражение функции не входит.
Понятие покрытия
Определение. Если на каком-либо наборе f принимает значение а_{1}, а  – значение а_{2}, то говорят, что f своим значением а_{1} покрывает значение а_{2} функции
– значение а_{2}, то говорят, что f своим значением а_{1} покрывает значение а_{2} функции 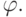
При минимизации ФАЛ стремятся получить форму, в которой будет меньше букв, чем в исходной. По отношению к ДНФ эта форма называется сокращенной (Сок. ДНФ).
Смысл построения Сок. ДНФ заключается в том, что в нее входят такие элементарные произведения, которые своими единицами покрывают не одну единицу исходной функции, а несколько.
Так, каждое элементарное произведение, входящее в СДНФ, покрывает только одну единицу функции.
Например:

1 1 1
Эти единицы функции могут быть накрыты более короткими произведениями: Х_{1} накрывает две единицы:  и
и  и
и  , которое накрывает также две единицы:
, которое накрывает также две единицы:  и
и  , т.е.
, т.е.



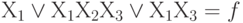 : здесь
: здесь 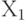 - простая
- простая  и
и  - не простые.
- не простые.