| Россия |
Акселерометры и гироскопы. Вибрационные и хроматографические сенсоры
Ответы
Ответы на вопросы
1. Акселерометрами называют сенсоры, которые реагируют на механическое ускорение тел и измеряют его. Основными видами акселерометров являются сенсоры линейного и сенсоры углового ускорения.
2. Первичным информационным сигналом в микроэлектронном ёмкостном сенсоре линейного ускорения является линейное ускорение объекта, на котором он установлен, точнее проекция вектора этого ускорения на ось акселерометра. Благодаря подвижной инертной массе ускорение преобразуется в линейное смещение инертной массы, а последнее – в изменение электрических ёмкостей между этой массой и неподвижными электродами. В результате на выходе мостовой схемы появляется электрический сигнал в виде изменения выходного напряжения. Этот сигнал может далее превращаться в цифровой сигнал, в перемещение стрелки на шкале и т.д.
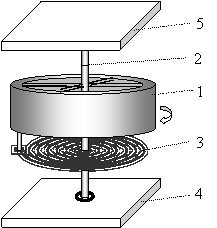
3. Гироскоп предназначен для надежного "хранения" и задания неизменного "эталонного" ("опорного") направления в пространстве, относительно которого и надо отсчитывать ускорение, скорости и углы крена или поворота контролируемого объекта. Гироскоп сохраняет направление своей оси несмотря на любые маневры контролируемого объекта в пространстве (ракеты, самолета, корабля, автомобиля, ...). Гироскоп состоит из ротора с достаточно большим моментом инерции, который быстро вращается вокруг своей оси. Ось установлена на кардановом подвесе или же весь гироскоп свободно плавает в жидкости. Благодаря этому и в соответствии с законом инерции ротор поддерживает направление оси вращения неизменным, а свою ориентацию относительно объекта при его поворотах в пространстве может свободно менять.
4. "Инерциальной платформой" называют систему отсчета, связанную с осью вращения гироскопа и рамкой, на которую она опирается. Установленные на ней сенсоры угла поворота, крена, линейного и углового ускорения выдают результаты отсчета углов относительно неизменного "эталонного" направления в пространстве.
5. Для уменьшения трения к точкам опоры осей гироскопа подводят воздух или инертный газ под высоким давлением, который, создавая газовую прослойку между осью и опорой, значительно уменьшает трение в оси по сравнению с любой смазкой. Гироскопы такой конструкции называют гироскопами на воздушных (газовых) подвесках или на аэродинамических подшипниках. Вращающийся ротор гироскопа может и просто висеть в воздухе или в вакууме за счет электростатических или магнитных сил, которые компенсируют гравитацию. Гироскопы такой конструкции соответственно называют "электростатическими" или "на магнитных подвесках". "Поплавковыми" называют гироскопы, ротор которых, заключенный в герметичную сферу, свободно плавает в жидкости с высокой плотностью.
Благодаря таким усовершенствованиям удается повысить временнyю стабильность положения оси гироскопа от 10–2 угловых градусов в час до 10–4  /ч и даже 10–5
/ч и даже 10–5  /ч.
/ч.
6. По закону инерции свою ориентацию в пространстве стремятся сохранять не только быстро вращающиеся тела, но и системы, в которых происходят механические колебания. В то же время с помощью МСТ гораздо легче сделать вибрирующие с большой частотой детали, чем быстро вращающиеся вокруг своей оси роторы и опорные микро- и тем более наноподшипники для них. Поэтому применение не ротационных, а именно колебательных или вибрационных узлов оказалось значительно перспективнее при изготовлении микромеханических гироскопов и акселерометров.
7. Главным недостатком микромеханических гироскопов-акселерометров является низкая временнaя стабильность направления главной оси гироскопа – порядка нескольких угловых градусов в час. Однако эти гироскопы-акселерометры имеют и очень важные преимущества: сравнительно низкую цену; малые габариты и массу; высокую надежность. Они потребляют ничтожную энергию, имеют высокую стойкость против вибраций и ударов. А с недостаточно высокой временнoй стабильностью успешно борются. Для этого на относительно спокойных интервалах движения определяют направление ускорения земного тяготения и по этим данным автоматически корректируют направление ориентации "виртуальной инерциальной платформы". Ее коррекцию можно выполнить также и по данным систем навигации GPS. Примеры применения: а) американская Draper Laboratory использует микромеханический гироскоп-акселерометр с микропроцессором в своем астроинерциальном комплексе для автоматической наводки телескопа, установленного на искусственном спутнике Земли, на нужные звезды и для длительной стабилизации положения этих звёзд в поле зрения телескопа; б) фирма Robert Bosch Gmb разработала на их основе сенсоры для быстрой реакции на опасность опрокидывания или закручивания автомобиля вокруг вертикальной оси с целью его немедленной автоматической электронной стабилизации.
8. Кантилевер представляет собой упругую длинную балку, закрепленную на одном конце, напоминающую трамплин для прыжков в воду. Такая балка имеет собственную основную частоту колебаний. На верхней поверхности кантилевера вблизи свободно колеблющегося конца формируют чувствительную зону, на которую наносят "рецепторный слой" – покрытие, избирательно чувствительное к тому или иному аналиту (например, к определенным микробам, антителам, молекулам). Вблизи закрепленного конца формируют пьезорезистор, а снизу наносят электрод, предназначенный для электростатического возбуждения механических колебаний кантилевера. Когда к чувствительному покрытию присоединяется аналит, то частота колебаний кантилевера изменяется. Поскольку встроенными в тот же кристалл кремния микросхемами воспринимаются и фиксируются даже очень незначительные изменения частоты, то чувствительность таких вибрационных сенсоров оказалась очень высокой – до единиц фемтограмм аналита (10–15 г).
9. Виброанализ основан на том, что каждая механическая конструкция имеет свои резонансные частоты, свои характерные колебательные свойства. При механических повреждениях, деформациях или других отклонениях от нормы картина собственных колебаний изделия изменяется. Это создает принципиальную возможность по изменению картины механических колебаний обнаруживать нежелательные изменения и дефекты, которые появились в конструкции. Одним из основных методов, помогающих разобраться в сложных колебаниях машин и механизмов, представляющих собой суперпозицию многих колебательных составляющих, является спектральный анализ. Наличие в составе вибрационного сенсора встроенного микропроцессора, памяти и матричного дисплея позволило выполнять спектральный анализ механических колебаний непосредственно в сенсоре и выводить на дисплей не только интегральные параметры колебаний, но и их частотные спектры. Стало возможным наглядно видеть частотную структуру колебаний, связанную с основными механическими движениями отдельных узлов и деталей контролируемого механизма, быстро выявить источник нежелательных или полезных изменений.
10. Хроматографические сенсоры мы относим к классу механических потому, что в них первичные сигналы появляются вследствие механического перемещения молекул и соответствующих веществ относительно неподвижной основы (фазы). Хроматографические сенсоры обычно применяют тогда, когда надо контролировать или выяснить химический состав смеси веществ с достаточно близкими физическими и химическими свойствами. Принцип их действия состоит в том, что в неподвижный сорбент вводят пробу контролируемой смеси и подвижную фазу ("проявитель") – жидкость или газ. Проявитель захватывает контролируемую смесь и продвигает её сквозь неподвижный сорбент. Поскольку вещества, из которых состоит смесь, несколько по-разному связываются с сорбентом и с проявителем, то и скорость их переноса вдоль колонки с сорбентом оказывается несколько разной. И в ходе продвижения они постепенно разделяются в пространстве. Первым выходит из хроматографической колонки вещество, у которого связь с проявителем по сравнению со связью с сорбентом наиболее сильная. На выходе из колонки устанавливают детектор, с помощью которого определяют скорость выхода веществ, и рисуют хроматограмму – зависимость от времени скорости выхода веществ из колонки. Хроматограмма позволяет определить состав смеси и удельное содержание в ней различных компонентов. Для надежности хроматографическую колонку предварительно калибруют по интересующим пользователя компонентам, пропуская через колонку смеси заранее точно известного состава.
11. В газовой хроматографии подвижной фазой (элюентом) является газ – именно он под давлением продвигает смесь сквозь колонку. В жидкостной хроматографии элюентом является жидкость.
12. Жидкость может стать неподвижной фазой, если ее механически фиксируют на какой-либо твердой основе, которую называют "матрицей" и на которой жидкость надежно удерживается при пропускании элюента.
Ответы к упражнениям
Упражнение 4.1. Принципиальная механическая схема акселерометра, измеряющего линейное ускорение, имеет вид:
Здесь М – инертная масса, У – упругий элемент, Д – демпфер. Инертная масса М может двигаться лишь вдоль одной прямой, в данном случае горизонтальной, которую называют осью акселерометра. Если объект, на котором установлен акселерометр, движется с ускорением, то под действием силы инерции масса М смещается, деформируя упругий элемент. Таким образом, инертная масса преобразует первичный информационный сигнал ускорения в перемещение или в силу деформации упругого элемента. Упругий элемент обеспечивает взаимную однозначность этого преобразования, обычно даже его линейность. Чтобы в этой механической системе не возникали медленно затухающие колебания, используется демпфер Д. Он превращает энергию колебаний в тепло и предотвращает возникновение длительных колебаний системы. При правильно подобранном демпфере инертная масса М быстро подходит к новому положению равновесия и останавливается в нем.
Движение инертной массы М описывается дифференциальным уравнением 2-го порядка:

 – отклонение инертной массы
– отклонение инертной массы  от положения равновесия;
от положения равновесия;  – коэффициент затухания, обусловленный демпфированием;
– коэффициент затухания, обусловленный демпфированием;  – коэффициент жесткости упругого элемента;
– коэффициент жесткости упругого элемента;  – текущее ускорение контролируемого объекта, на котором установлен акселерометр.
– текущее ускорение контролируемого объекта, на котором установлен акселерометр.Чтобы определить ускорение а, достаточно измерить либо отклонение  от положения равновесия, либо силу
от положения равновесия, либо силу  , действующую на упругий элемент.
, действующую на упругий элемент.
Упражнение 4.2. Принципиальная механическая схема акселерометра, измеряющего угловое ускорение, имеет вид, показанный на рисунке. Здесь 1 – ротор с достаточно большим моментом инерции относительно оси вращения 2; 3 – упругий элемент закручивания, 4 и 5 – опоры оси вращения. Нужен также демпфер, который гасит энергию возникающих крутильных колебаний.
Если контролируемый объект вращается с угловым ускорением вокруг направления оси акселерометра, то ротор 1 под действием момента инерции поворачивается на определенный угол. Измеряя угол закручивания или момент силы на упругом элементе, можно определить величину углового ускорения. Таким образом, ротор преобразует первичный информационный сигнал углового ускорения в поворот или в момент деформации упругого элемента. Упругий элемент обеспечивает взаимную однозначность этого преобразования, обычно – линейность. При правильно подобранном демпфере ротор 1 быстро поворачивается в новое положение равновесия и останавливается в нем.
Упражнение 4.3. Акселерометр или сенсор угла поворота вовсе не обязательно устанавливать на инерциальной платформе, жестко связанной с осью вращения ротора и рамкой, на которую она опирается, сохраняющей свою исходную ориентацию в пространстве. Альтернативный подход состоит в том, что на двух вспомогательных осях карданова подвеса устанавливают сенсоры, измеряющие углы поворота объекта относительно его исходной ориентации. Тогда акселерометр или угломер могут быть установлены непосредственно на контролируемом объекте, что конструктивно проще. А результаты измерения ускорений и углов, которые они выдают, по известным формулам перехода от одной системы координат к другой всегда могут быть пересчитаны в ускорение или в углы относительно исходной или произвольной третьей системы координат. Но для этого сенсор, в состав которого входят и акселерометр, и гироскоп, должен быть интеллектуальным, т.е. включать в свой состав микрокомпьютер. Такой подход и называют использованием "виртуальной инерциальной платформы".
Формулы пересчета ускорений  , измеряемых трехосным акселерометром, установленным на раме контролируемого объекта, в ускорения
, измеряемых трехосным акселерометром, установленным на раме контролируемого объекта, в ускорения  относительно исходной системы координат, используя измеряемые углы
относительно исходной системы координат, используя измеряемые углы  и
и  поворота рамок карданового подвеса гироскопа, можно записать так:
поворота рамок карданового подвеса гироскопа, можно записать так:

Наиболее просто получить их посредством перемножения т.н. "матриц вращения в 3-мерном пространстве".
Упражнение 4.4.
Вариант 1. Сначала учтем, что 9 месяцев составляет 273-275 дней, т.е. около 275 \times; 24 = 6600 часов. Предельное отклонение оси гироскопа от исходного направления после 9 месяцев полета космического корабля к Марсу при стабильности положения оси 10–4  /ч составляет 10–4 x 6600 = 0,66
/ч составляет 10–4 x 6600 = 0,66  .
.
Вариант 2. Учитывая то, что 15 месяцев составляет около 640 дней, т.е. около 640x24 = 15360 часов, находим предельное отклонение оси гироскопа от исходного направления после 15 месяцев автономного плавания атомной подводной лодки при стабильности положения оси 10–5  /ч. Оно составляет 10–5 x 15360 = 0,15
/ч. Оно составляет 10–5 x 15360 = 0,15  .
.
Вариант 3. В произвольный момент времени  ракета находится на расстоянии
ракета находится на расстоянии 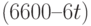 км от цели. За время
км от цели. За время 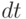 направление её движения может дополнительно отклониться на угол
направление её движения может дополнительно отклониться на угол  радиан. Эта погрешность создает возможность дополнительного отклонения от цели на расстояние
радиан. Эта погрешность создает возможность дополнительного отклонения от цели на расстояние  . Время полета составляет
. Время полета составляет 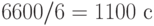 . За это время суммарное предельное отклонение ракеты от цели, обусловленное временнoй нестабильностью положения оси её гироскопа, может составить
. За это время суммарное предельное отклонение ракеты от цели, обусловленное временнoй нестабильностью положения оси её гироскопа, может составить
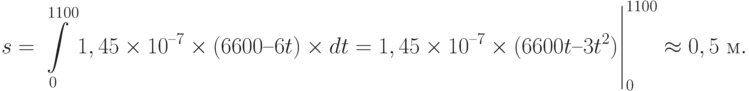
Упражнение 4.5. Вариант 1. В соответствии с формулой (4.3) изменение частоты (в Гц) можно рассчитать по формуле

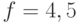 МГц – исходная частота колебаний;
МГц – исходная частота колебаний;  г – прирост массы;
г – прирост массы;  см2 – площадь электрода пьезокристалла. Подставляя эти данные, получаем
см2 – площадь электрода пьезокристалла. Подставляя эти данные, получаем
Вариант 2. Из формулы (4.3) следует, что
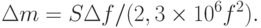
Подставляя данные из задачи, находим
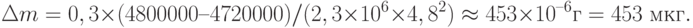
Вариант 3. Из формулы (4.3) следует, что

Подставляя данные из задачи, находим теоретическую чувствительность микровесов