| Россия |
Рекурсия и деревья
8.3. Рекурсия как стратегия решения задач
В предыдущих лекциях мы рассматривали управляющие структуры языка программирования как технику, используемую для решения сложных задач.
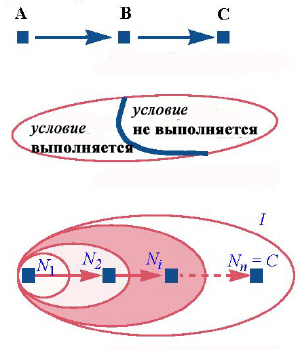
- Составной оператор (последовательность). Семантику последовательности можно выразить так: "Я знаю кого-то, кто может провести меня от текущей точки до В, и знаю того, кто может провести от В до С, так что можно просить их, работая последовательно, провести меня до С".
- Условный оператор означает: "Я знаю кого-то, кто может решить задачу в одном случае, и знаю того, кто может решить ее для всех других возможных случаев, что позволяет мне просить их работать в зависимости от возникающей ситуации".
- Решение, использующее цикл, можно выразить так: "Я не знаю, как добраться до С, но я знаю область I (инвариант), содержащую С, знаю кого-то, кто может привести меня в эту область (инициализация), и знаю того (тело цикла), кто может приблизить меня к С, при условии, что я нахожусь в области I. Расстояние до цели будет уменьшаться (вариант) таким образом, что за конечное число шагов я достигну требуемой мне окрестности С. Мне остается попросить моего первого друга привести меня в область I, а затем просить второго друга приближать меня к С, пока я не достигну цели".
- Процедура, как способ решения задачи, означает: "Я знаю кого-то, кто может решать эту задачу в общем случае, так что мне нужно лишь сформулировать мою специальную задачу в его терминах и попросить решить задачу для меня".
Что можно сказать о рекурсивном решении? К кому нужно обращаться? Ответ – к себе! Возможно – несколько раз (как в случае с Ханойской башней и многих других)!
Зачем обращаться к другим, если я доверяю себе (по крайней мере, я так думаю)?
Теперь мы знаем, что эта стратегия не так глупа, как может казаться с первого раза. Я прошу себя решить ту же задачу, но на подмножестве исходных данных или на нескольких таких подмножествах. Тогда я могу справиться с задачей, если удастся частные решения объединить в решение задачи в целом.
Такова идея рекурсии, рассматриваемая как стратегия решения сложной задачи. Она связана с некоторыми предыдущими стратегиями.
- Рекурсия предполагает процедурную стратегию, так как она основана на решении той же задачи.
- Она использует свойства циклической стратегии: оба подхода приближают решение полной проблемы, покрывая решение расширяющегося множества данных. Но дает более общий подход, так как на каждом шаге может комбинироваться несколько частных решений. Позже мы детально сравним стратегии цикла и рекурсии.
8.4. Бинарные деревья
Если Ханойская башня является квинтэссенцией рекурсивной процедуры, то бинарные деревья являются квинтэссенцией рекурсивных структур данных. Их можно определить следующим образом:
Определение: бинарное дерево
Бинарное дерево над G, для произвольного типа данных G, задается конечным множеством элементов, называемых узлами, каждый из которых содержит значение типа G. Узлы, если они есть, разделяются на три непересекающихся подмножества:
- единственный узел, называемый корнем бинарного дерева;
- (рекурсивно) два бинарных дерева над G, называемых левым поддеревом и правым поддеревом.
Все это просто выразить в каркасе класса, не включающем методов:
class BINARY_TREE [G] feature
item: G
left, right: BINARY_TREE[G]
end
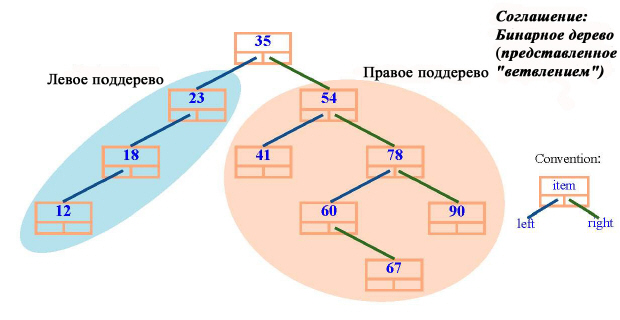
Ссылка void указывает на пустое дерево. Проиллюстрируем бинарное дерево над целыми ( рис. 8.9).
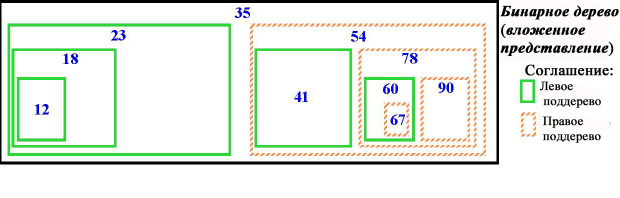
Форма "Ветвления" – это наиболее общий стиль представления бинарных деревьев, но не единственный: возможно представление в форме вложенности, которое для данного примера выглядит так ( рис. 8.10).
Определение бинарного дерева явно допускает, что дерево может быть пустым. Без этого, конечно, рекурсивное определение приводило бы к бесконечной структуре, в то время как бинарные деревья, что также предписано определением, являются конечными структурами данных.
Если бинарное дерево не пусто, то оно всегда имеет корень и может не иметь поддеревьев, иметь только левое или только правое поддерево или иметь оба поддерева.
Любой узел бинарного дерева сам рассматривается как бинарное дерево. Достаточно взглянуть на два последних рисунка. Узел, помеченный как 35, задает полное дерево, 23 – его левое поддерево, 54 – правое. Узел 78 задает корень дерева, которое является правым поддеревом правого поддерева полного дерева. Это позволяет говорить о правом и левом поддереве каждого узла. Эту ассоциацию можно сделать формальной, дав другой пример рекурсивного определения.
Определение: дерево, ассоциированное с узлом
 бинарного дерева
бинарного дерева  определяет бинарное дерево
определяет бинарное дерево  следующим образом:
следующим образом:
- если
 – корень
– корень  , то
, то  – это просто
– это просто  ;
; - в противном случае из предыдущего определения следует, что
 – это одно из поддеревьев
– это одно из поддеревьев  . Если
. Если 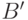 – это поддерево, то определим
– это поддерево, то определим  как
как 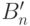 (узел, связанный с
(узел, связанный с  , рекурсивно, в соответствующем поддереве).
, рекурсивно, в соответствующем поддереве).
Рекурсивные процедуры над рекурсивными структурами данных
Большинство методов класса, определяющего рекурсивную структуру класса, будут строиться рекурсивно с учетом рекурсивного определения данных. Простым примером является метод, подсчитывающий число узлов бинарного дерева. В пустом дереве число узлов равно нулю, для непустого дерева число узлов равно сумме трех значений: для корня и числа узлов соответственно левого и правого поддеревьев. Нетрудно записать это наблюдение в виде рекурсивной функции, входящей в класс BINARY_TREE.
count: INTEGER
— Число узлов.
do
Result := 1
if left /= Void then Result := Result + left.count end
if right /= Void then Result := Result + right.count end
end
Заметьте схожесть этой функции с процедурой Hanoi.