| Россия, Санкт-Петербург, Северо-Западный заочный технический университет, 2007 |
Хэш-функции
Хэш-функция MD5
Рассмотрим алгоритм получения дайджеста сообщения MD5 (RFC 1321), разработанный Роном Ривестом из MIT.
Алгоритм получает на входе сообщение произвольной длины и создает в качестве выхода дайджест сообщения длиной 128 бит. Алгоритм состоит из следующих шагов:
Шаг 1: добавление недостающих битов
Сообщение дополняется таким образом, чтобы его длина стала равна 448 по модулю 512 (длина = 448 (mod 512)). Это означает, что длина добавленного сообщения на 64 бита меньше, чем число, кратное 512. Добавление производится всегда, даже если сообщение имеет нужную длину. Например, если длина сообщения 448 битов, оно дополняется 512 битами до 960 битов. Таким образом, число добавляемых битов находится в диапазоне от 1 до 512.
Добавление состоит из единицы, за которой следует необходимое ко-личество нулей.
Шаг 2: добавление длины
64-битное представление длины исходного (до добавления) сообщения в битах присоединяется к результату первого шага. Если первоначальная длина больше, чем 264, то используются только последние 64 бита. Таким образом, поле содержит длину исходного сообщения по модулю 264.
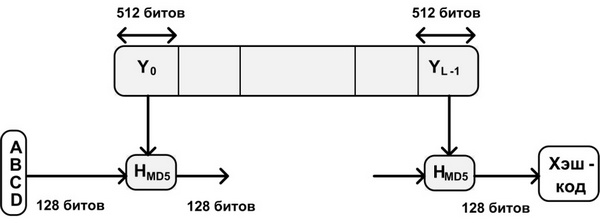
В результате первых двух шагов создается сообщение, длина которого кратна 512 битам. Это расширенное сообщение представляется как после-довательность 512-битных блоковY0, Y1, . . ., YL-1, при этом общая длина расширенного сообщения равна L * 512 битам. Таким образом, длина полученного расширенного сообщения кратна шестнадцати 32-битным словам.
Шаг 3: инициализация MD-буфера
Используется 128-битный буфер для хранения промежуточных и окон-чательных результатов хэш-функции. Буфером являются четыре 32-битных регистра (A, B, C, D). Эти регистры инициализируются следующими шестнадцатеричными числами:
А = 01234567
В = 89ABCDEF
C = FEDCBA98
D = 76543210
Шаг 4: обработка последовательности 512-битных (16-словных) блоков
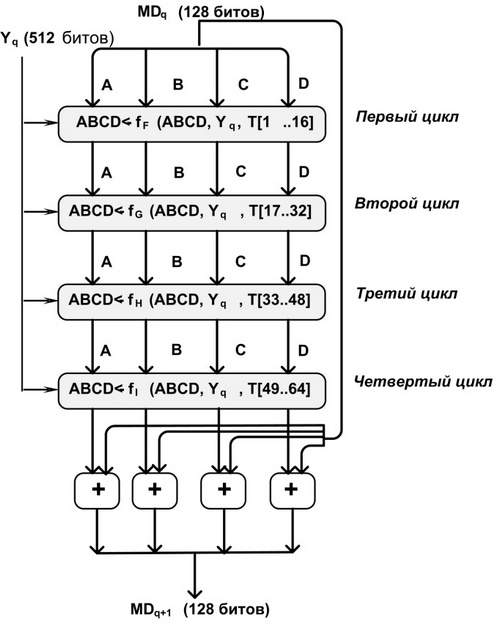
Основой алгоритма является модуль, состоящий из четырех циклических обработок, обозначенный как HMD5. Четыре цикла имеют похожую структуру, но каждый цикл использует свою элементарную логическую функцию, обозначаемую fF, fG, fH и fI соответственно (рис. 3.3).
Каждый цикл принимает в качестве входа текущий 512-битный блок Yq, обрабатывающийся в данный момент, и 128-битное значение буфера ABCD, которое является промежуточным значением дайджеста, и изменяет содержимое этого буфера. На каждом цикле также используется четвертая часть 64-элементной таблицы T[1] ... T[64], построенной на основе функции sin.
![T[i] = [2^3^2 * abs (sin(i))]](/sites/default/files/tex_cache/8231280de5b688e3d46dca4b90337598.png)
Где [ ] в правой части означает целую часть числа, i задано в радианах. Так как abs (sin(i))является числом между 0 и 1, каждый элемент Т [i] является целым, которое может быть представлено 32 битами. Таблица обеспечивает "случайный" набор 32-битных значений, которые должны ликвидировать любую регулярность во входных данных.
Для получения MDq+1 выход четырех циклов складывается по модулю 232 с MDq. Сложение выполняется независимо для каждого из четырех слов в буфере.
Шаг 5: выход
После обработки всех L 512-битных блоков выходом L-ой стадии является 128-битный дайджест сообщения.
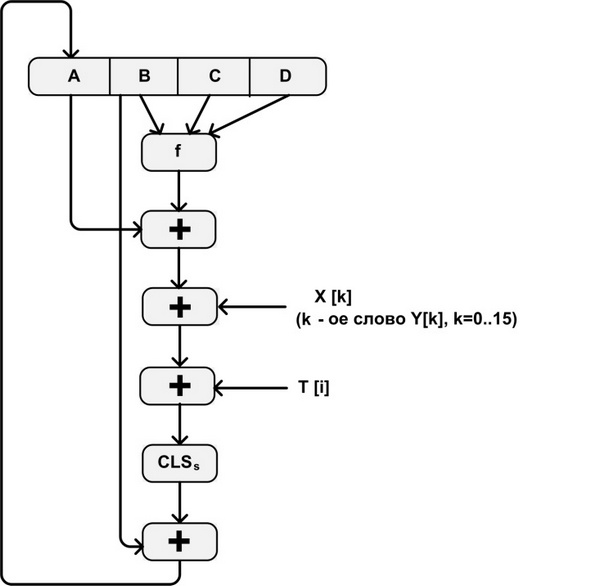
Рассмотрим более детально логику каждого из четырех циклов выполнения одного 512-битного блока. Каждый цикл состоит из 16 шагов, оперирующих с буфером ABCD. Каждый шаг представлен на рис. 3.4.
![A \leftarrow B + CLS_s (A + f (B, C, D) + X [k] + T [i])](/sites/default/files/tex_cache/ea60bd9ce9f38c847fd832dcff5f36c1.png)
где A, B, C, D - четыре слова буфера; после выполнения каждого отдельного шага происходит циклический сдвиг влево на одно слово.
f - одна из элементарных функций fF, fG, fH, fI.
CLSs- циклический сдвиг влево на s битов 32-битного аргумента.
X[k] - M[q*16 + k] - k-ое 32-битное слово в q-ом 512 блоке сообщения.
T[i]- i-ое 32-битное слово в таблице Т.
+ - сложение по модулю 232.
В каждом из четырех циклов алгоритма используется одна из четырех так называемых элементарных логических функций. Каждая элементарная функция получает три 32-битных слова на входе и на выходе создает одно 32-битное слово. Каждая функция является набором побитовых логических операций, т.е. n-ый бит выхода является функцией от n-ого бита трех входов. Элементарные функции следующие:

Массив из 32-битных слов X[0..15] содержит значение текущего 512-битного входного блока, который обрабатывается в настоящий момент. Каждый цикл выполняется 16 раз, а так как каждый блок входного сообщения обрабатывается в четырех циклах, то каждый блок входного сообщения обрабатывается по описанной выше схеме 64 раза. Если представить входной 512-битный блок в виде шестнадцати 32-битный слов, то каждое входное 32-битное слово используется четыре раза, по одному разу в каждом цикле, и каждый элемент таблицы Т, состоящей из 64 32-битных слов, используется только один раз. После каждого шага цикла происходит циклический сдвиг влево четырех слов A, B, C и D. На каждом шаге изменяется только одно из четырех слов буфера ABCD. Следовательно, каждое слово буфера изменяется 16 раз, и затем 17-ый раз в конце для получения окончательного выхода данного блока.
Можно суммировать алгоритм MD5 следующим образом:
![MD_0 = IV\\
MD_q_+_1 = MD_q+f_I[ Y_q, f_H[ Y_q, f G[Y_q, f_F[Y_q, MD_q] ] ] ]\\
MD = MD_L-_1](/sites/default/files/tex_cache/b6136577cc8e35187808d8c46e9fba7a.png)
Где
IV - начальное значение буфера ABCD, определенное на шаге 3.
Yq - q-ый 512-битный блок сообщения.
L - число блоков в сообщении (включая поля дополнения и длины).
MD - окончательное значение дайджеста сообщения.