Разработка простых цифровых устройств
Разработка вычислителя контрольной суммы
Различные контрольные суммы широко применяются в цифровых устройствах и системах для контроля правильности хранения или передачи массивов информации. Суть этого метода контроля проста: к хранимому или передаваемому информационному массиву присоединяется небольшой контрольный код (обычно от 1 разряда до 32 разрядов), в котором в свернутом виде содержится информация обо всем массиве. При чтении или получении этого массива еще раз вычисляется тот же самый контрольный код по тому же самому алгоритму. Если этот вновь вычисленный код равен тому коду, который был присоединен к массиву, то считается, что массив сохранен или передан без ошибок. Логика здесь следующая: контрольный код (он же контрольная сумма ) гораздо меньше контролируемого массива, поэтому вероятность искажения контрольной суммы гораздо меньше, чем вероятность искажения массива. Если же исказятся как массив, так и контрольная сумма, то вероятность того, что эти искажения не будут замечены при повторном подсчете контрольной суммы, крайне мала. Существует, правда, вероятность, что массив будет искажен в нескольких местах таким образом, что контрольная сумма от этих искажений никак не изменится, но такая вероятность также обычно мала.
Контрольные суммы применяются при хранении данных в памяти (оперативной и постоянной), при хранении данных на магнитных носителях (дисках, лентах), в локальных и глобальных сетях передачи информации. В случае защиты контрольной суммой хранимой информации можно определить, что данный массив (файл, сектор на диске) испорчен и его нельзя использовать. В случае защиты контрольной суммой передаваемой по сети информации приемник может потребовать от передатчика повторной передачи искаженного массива.
Существует множество способов вычисления контрольной суммы, различающихся степенью сложности вычисления и надежностью выявления ошибок. Но наибольшее распространение получил в настоящее время так называемый "циклический метод контроля по избыточности" или CRC (Cyclic Redundancy Check), при котором применяется циклическая контрольная сумма.
Вычисляется циклическая контрольная сумма следующим образом. Весь массив информации рассматривается как одно N-разрядное двоичное число, где N — количество бит во всех байтах массива. Для вычисления контрольной суммы это N-разрядное число делится на некоторое постоянное число ( полином ), выбранное специальным образом (но делится не просто, а по модулю 2). Частное от этого деления отбрасывается, а остаток как раз и используется в качестве контрольной суммы.
Мы не будем углубляться в математическое обоснование этого метода. Интересующиеся читатели могут обратиться к специальной литературе. Здесь же мы отметим только, что данный метод выявляет одиночные ошибки в массиве с вероятностью 100%, а любое другое количество ошибок с вероятностью, примерно равной 1–2-n, где n — количество разрядов контрольной суммы (это верно только при условии, что N гораздо больше n, что, впрочем, почти всегда выполняется). Например, при n = 8 данная вероятность составит 0,996, для n = 16 она будет равна 0,999985, а для n = 32 она будет 0,9999999997672. Иначе говоря, почти все ошибки будут выявляться.
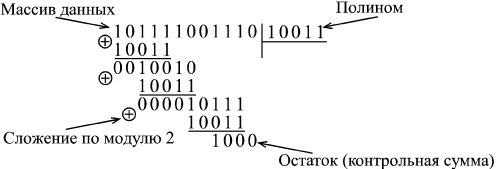
А теперь кратко поясним, что такое деление по модулю 2. Пусть массив (последовательность бит) имеет следующий вид: 101111001110 (для простоты берем небольшую разрядность). Число, на которое делим (называемое обычно образующим полиномом ) возьмем 10011. Как оно выбирается? Оно должно делиться по модулю 2 без остатка только на единицу и само на себя (то есть это должно быть простое число в смысле деления по модулю 2). Разрядность полинома берется на единицу большая, чем требуемая разрядность контрольной суммы (остатка от деления). Так, чтобы получить 8-разрядный остаток (8-разрядную контрольную сумму), надо брать 9-разрядный полином. В нашем случае полином 5-разрядный, следовательно, остаток будет 4-разрядный. Для получения 8-разрядного остатка можно использовать, например, полином 1 0001 1101 или 11D в 16-ричном коде.
Деление по модулю 2 производится точно так же, как и привычное для нас деление "в столбик" (рис. 14.6), но вместо вычитания в данном случае используется поразрядное сложение по модулю 2, то есть каждый результирующий бит представляет собой функцию Исключающее ИЛИ от соответствующих битов слагаемых. Частное от деления нас не интересует, а остаток, равный в нашем примере 1000, и будет циклической контрольной суммой.
Как практически реализовать вычисление этого остатка (контрольной суммы)? Можно сделать это по приведенному здесь принципу деления в столбик (аппаратно или программно). Но в любом случае это довольно громоздко и медленно. Ускорить процесс вычисления можно, воспользовавшись табличным методом. Для этого составляется таблица чисел размером 2nхn, где n — разрядность контрольной суммы. Принцип вычисления чисел в таблице очень прост (табл. 14.1).
| Адрес в таблице | Данные в таблице (числа) |
|---|---|
| 0 | 0 |
| 1 | Остаток от деления числа 1 0000 0000 на полином |
| 2 | Остаток от деления числа 10 0000 0000 на полином |
| 3 | Остаток от деления числа 11 0000 0000 на полином |
| 4 | Остаток от деления числа 100 0000 0000 на полином |
| 5 | Остаток от деления числа 101 0000 0000 на полином |
 |
 |
| 255 | Остаток от деления числа 1111 1111 0000 0000 на полином |
Числа представляют собой остаток от деления по модулю 2 числа с n конечными нулями (в нашем примере n = 8) и с n начальными разрядами, равными номеру числа (его адресу) в таблице. Деление производится на выбранный полином (в нашем случае — 9-разрядный). Таблица вычисляется один раз и хранится на диске или в ПЗУ.
Алгоритм вычисления контрольной суммы с помощью этой таблицы следующий (рассматриваем случай n = 8). Берем первый байт нашего информационного массива. Рассматриваем его как адрес в таблице (номер числа). Берем из таблицы число с полученным номером — получаем остаток О1. Берем второй байт массива и складываем его по модулю 2 с остатком О1. Полученное число используем как адрес в таблице. По этому адресу выбираем из таблицы остаток О2. Берем третий байт массива, складываем его по модулю 2 с остатком О2. Используя это число как адрес в таблице, выбираем из нее остаток О3 и так продолжаем до последнего байта массива. Естественно, это будет гораздо быстрее, чем вычисление "в столбик".
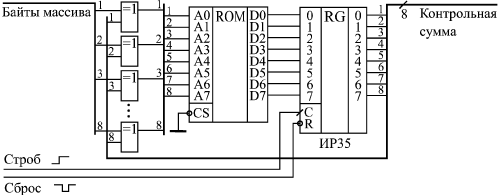
Реализация этого алгоритма с помощью цифровых схем требует только ПЗУ с организацией 2nхn (256х8 при 8-разрядной контрольной сумме), n-разрядного регистра и n элементов Исключающее ИЛИ (рис. 14.7). В ПЗУ заносится таблица промежуточных остатков (табл. 14.1), на вход схемы подаются один за другим байты массива, сопровождаемые стробом. Адресом ПЗУ служит сумма по модулю 2 входных данных и содержимого выходного регистра, в который по сигналу строба записывается выходной код ПЗУ. Перед началом вычисления состояние регистра обнуляется. После окончания всего массива в регистре образуется циклическая контрольная сумма.
Недостаток данной схемы параллельного вычислителя очевиден: в случае большого числа разрядов контрольной суммы требуется очень большой объем ПЗУ (64Кх16 для 16-разрядной суммы и 4Гх32 для 32-разрядной суммы). Поэтому она применяется сравнительно редко. Зато параллельный вычислитель обладает высоким быстродействием (байты могут поступать с периодом, равным сумме задержки выходного регистра, времени выборки адреса ПЗУ и задержки элемента Исключающее ИЛИ).
Для многоразрядной контрольной суммы чаще применяется другой подход — вычисление в последовательном коде, при котором массив данных поступает на вычислитель последовательно, бит за битом. Последовательный вычислитель контрольной суммы представляет собой сдвиговый регистр с обратными связями от некоторых разрядов через сумматоры по модулю 2 (то есть элементы Исключающее ИЛИ). Полное количество разрядов регистра сдвига должно быть равно разрядности вычисляемой контрольной суммы (или, что то же самое, быть на единицу меньше разрядности используемого полинома). Место включения обратных связей однозначно определяется выбранным полиномом. Это очень похоже на генератор квазислучайной последовательности.
Количество точек включения обратной связи определяется количеством единиц в полиноме (единица в младшем разряде не учитывается), а номера разрядов сдвигового регистра, с которых берутся сигналы обратной связи, определяются номерами единичных разрядов в коде полинома. В отличие от генератора квазислучайного сигнала, в данном случае необходимо смешать по функции Исключающее ИЛИ не только сигналы обратной связи, но и входной сигнал данных в последовательном коде.
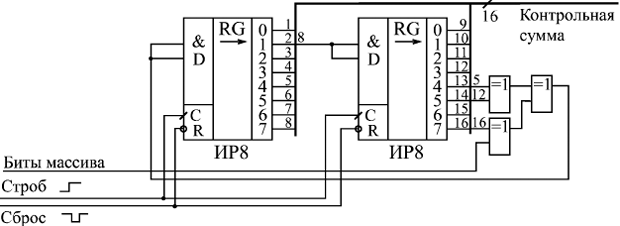
Рис. 14.8. Последовательный вычислитель 16-разрядной циклической контрольной суммы на регистре сдвига
На рис. 14.8 приведен пример последовательного вычислителя 16-разрядной циклической контрольной суммы при выбранном полиноме 1 0001 0000 0010 0001 или 11021 в 16-ричном коде (рекомендация МККТТ V.41). Так как в коде полинома три единицы (без младшего разряда), необходимо взять три точки включения обратной связи. При этом номера разрядов сдвигового регистра, к которым подключаются обратные связи, определяются положением единичных битов в полиноме. Перед началом работы сдвиговый регистр необходимо сбросить в нуль (сигнал "–Сброс"). Биты массива должны сопровождаться сигналом строба. После окончания массива в регистре будет циклическая контрольная сумма.
Может показаться, что такой последовательный вычислитель не слишком удобен из-за того, что данные массива должны подаваться на него в последовательном коде. Однако именно в последовательном коде передаются данные в информационных сетях, и в последовательном коде записываются данные на магнитные носители. Поэтому во всех подобных случаях последовательные вычислители идеально подходят.
Период поступления битов массива на последовательный вычислитель не должен быть меньше суммы задержки регистра сдвига и элементов Исключающее ИЛИ. В итоге предельная скорость вычисления циклической контрольной суммы оказывается значительно меньшей, чем в случае параллельного вычислителя. Это также недостаток данного метода вычисления.