Базовые понятия цифровой электроники
Уровни представления цифровых устройств
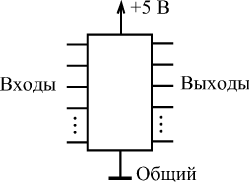
Все цифровые устройства строятся из логических микросхем, каждая из которых (рис. 1.3) обязательно имеет следующие выводы (или, как их еще называют в просторечии, "ножки"):
- выводы питания: общий (или "земля") и напряжения питания (в большинстве случаев — +5 В или +3,3 В), которые на схемах обычно не показываются;
- выводы для входных сигналов (или "входы"), на которые поступают внешние цифровые сигналы;
- выводы для выходных сигналов (или "выходы"), на которые выдаются цифровые сигналы из самой микросхемы.
Каждая микросхема преобразует тем или иным способом последовательность входных сигналов в последовательность выходных сигналов. Способ преобразования чаще всего описывается или в виде таблицы (так называемой таблицы истинности), или в виде временных диаграмм, то есть графиков зависимости от времени всех сигналов.
Все цифровые микросхемы работают с логическими сигналами, имеющими два разрешенных уровня напряжения. Один из этих уровней называется уровнем логической единицы (или единичным уровнем), а другой — уровнем логического нуля (или нулевым уровнем). Чаще всего логическому нулю соответствует низкий уровень напряжения, а логической единице — высокий уровень. В этом случае говорят, что принята "положительная логика". Однако при передаче сигналов на большие расстояния и в системных шинах микропроцессорных систем порой используют и обратное представление, когда логическому нулю соответствует высокий уровень напряжения, а логической единице — низкий уровень. В этом случае говорят об "отрицательной логике". Иногда логический нуль кодируется положительным уровнем напряжения (тока), а логическая единица — отрицательным уровнем напряжения (тока), или наоборот. Есть и более сложные методы кодирования логических нулей и единиц. Но мы в основном будем говорить о положительной логике.
Для описания работы цифровых устройств используют самые различные модели, отличающиеся друг от друга сложностью, точностью, большим или меньшим учетом тонких физических эффектов. В основном эти модели используются при компьютерных расчетах цифровых схем. В настоящее время существуют компьютерные программы, которые не только рассчитывают готовые схемы, но способны и проектировать новые схемы по формализованным описаниям функций, которые данное устройство должно выполнять. Это довольно удобно, но ни одна программа никогда не может сравниться с человеком. По-настоящему эффективные, минимизированные по аппаратуре, наконец, красивые схемы может разрабатывать только человек, который всегда подходит к проектированию творчески и использует оригинальные идеи.
Разработчик цифровой аппаратуры тоже использует своеобразные модели или, как еще можно сказать, различные уровни представления цифровых схем. Но, в отличие от компьютера, человек может гибко выбирать нужную модель — ему надо только взглянуть на схему, чтобы понять, где достаточно простейшей модели, а где требуется более сложная. То есть человек никогда не будет делать лишней, избыточной работы и, следовательно, не будет вносить дополнительных ошибок, свойственных любой, даже самой сложной, модели. Правда, простота цифровых устройств по сравнению с аналоговыми обычно не провоцирует на чересчур серьезные ошибки.
В подавляющем большинстве случаев для разработчика цифровых схем достаточно трех моделей, трех уровней представления о работе цифровых устройств:
- Логическая модель.
- Модель с временными задержками.
- Модель с учетом электрических эффектов (или электрическая модель).
Опыт показывает, что первой, простейшей модели достаточно примерно в 20% всех случаев. Она применима для всех цифровых схем, работающих с низкой скоростью, в которых быстродействие не принципиально. Привлечение второй модели, учитывающей задержки срабатывания логических элементов, позволяет охватить около 80% всех возможных схем. Ее применение необходимо для всех быстродействующих устройств и для случая одновременного изменения нескольких входных сигналов. Наконец, добавление третьей модели, учитывающей входные и выходные токи, входные и выходные сопротивления и емкости элементов, дает возможность проектирования практически 100% цифровых схем. В первую очередь, эту третью модель надо применять при объединении нескольких входов и выходов, при передаче сигналов на большие расстояния и при нетрадиционном включении логических элементов (с переводом их в аналоговый или в линейный режимы).
Для иллюстрации работы перечисленных моделей рассмотрим работу самого простейшего логического элемента - инвертора. Инвертор изменяет (инвертирует) логический уровень входного сигнала на противоположный уровень выходного сигнала или, как еще говорят, изменяет полярность логического сигнала. Его таблица истинности (табл. 1.1) элементарно проста, так как возможно только две ситуации: нуль на входе или единица на входе. На рис. 1.4 показано, как будет выглядеть выходной сигнал инвертора при использовании трех его моделей (трех уровней его представления). Такие графики логических сигналов называются временными диаграммами, они позволяют лучше понять работу цифровых схем.
Из рисунка видно, что в первой, логической модели считается, что элемент срабатывает мгновенно, любое изменение уровня входного сигнала сразу же, без всякой задержки приводит к изменению уровня выходного сигнала. Во второй модели выходной сигнал изменяется с некоторой задержкой относительно входного. Наконец, в третьей модели выходной сигнал не только задерживается по сравнению с входным, но и его изменение происходит не мгновенно - процесс смены уровней сигнала (или, как говорят, фронт сигнала ) имеет конечную длительность. Кроме того, третья модель учитывает изменение уровней логических сигналов.