|
Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2.? |
Комбинаторные задачи с ограничениями
Задачи о смещениях
Смещение элементов
Задача 1. Берутся все перестановки из пяти чисел 1,2,3,4,5 . Во скольких перестановках ни одно число не стоит на своем месте?
Решение методом включения-исключения.
Обозначим через  -свойство перестановки, заключающееся в том, что число
-свойство перестановки, заключающееся в том, что число  стоит на своем месте, а через
стоит на своем месте, а через 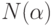 - количество перестановок, обладающих этим свойством.
- количество перестановок, обладающих этим свойством.
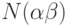 - число перестановок ,обладающих свойством
- число перестановок ,обладающих свойством 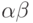
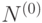 - число перестановок ,не обладающих ни одним из перечисленных свойств (1),(2),(3),(4) и (5), т.е. число перестановок в которых ни одно число не стоит на своем месте.
- число перестановок ,не обладающих ни одним из перечисленных свойств (1),(2),(3),(4) и (5), т.е. число перестановок в которых ни одно число не стоит на своем месте.
По формуле включения-исключения имеем:
 |
( 1) |
где  - общее число всех перестановок из пяти элементов.
- общее число всех перестановок из пяти элементов.
Задача облегчается тем ,что свойства (1),(2),(3),(4) и (5) совершенно равноправны ,поэтому ясно, что 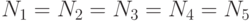 . Точно так же имеем
. Точно так же имеем 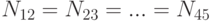 . Но число пар ,которые можно выбрать из чисел 1,2,3,4,5 -
. Но число пар ,которые можно выбрать из чисел 1,2,3,4,5 - 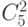 . Свойства (1,2) и (2,1) - совпадают ,поэтому порядок нас не интересует. Точно так же имеем
. Свойства (1,2) и (2,1) - совпадают ,поэтому порядок нас не интересует. Точно так же имеем  троек,
троек,  четверок,
четверок, 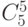 пятерок. Формулу (1) перепишем:
пятерок. Формулу (1) перепишем:
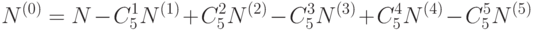 |
( 2) |
где  - количество перестановок ,в которых заданные
- количество перестановок ,в которых заданные  чисел остались на своих местах.
чисел остались на своих местах.
 - одно число на своем месте, остальные переставляются, т.е.
- одно число на своем месте, остальные переставляются, т.е. 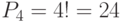 . Следовательно,
. Следовательно, 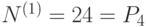 .
.
 - два числа на месте , три переставляются.
- два числа на месте , три переставляются.
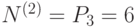 , аналогично
, аналогично  ;
; 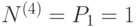 ;
;  . Подставляем в формулу (2).
. Подставляем в формулу (2).

Совершенно так же можно найти во скольких случаях ровно один элемент стоит на своем месте. Если это первый элемент , то

Общее количество способов ,при которых в точности один элемент стоит на своем месте, равно 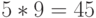 так как
так как 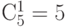 . Итак, можно посчитать , что в точности два элемента стоят на своих местах в 20-ти случаях, три - в 10-ти случаях, четыре - в 0 случаях, пятеро - в 1-ом случае:
. Итак, можно посчитать , что в точности два элемента стоят на своих местах в 20-ти случаях, три - в 10-ти случаях, четыре - в 0 случаях, пятеро - в 1-ом случае:
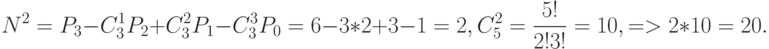
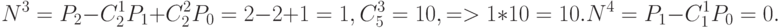
Результат для четырех элементов объясняется тем, что если четыре элемента стоят на своем месте, то и пятый должен стоять на своем месте. Итак 120 разных способов (перестановок из 5-ти элементов) распадаются на: 44 перестановки ,в которых ни один элемент не остается на месте , 45 перестановок ,в которых ровно один элемент не меняет своего положения, 20 перестановок ,в которых ровно два элемента не меняют своего положения, 10 перестановок ,в которых ровно три элемента не меняют своего положения, 0 перестановок ,в которых ровно четыре элемента не меняют своего положения, 1 перестановки, в которой ровно пять элементов не меняют своего положения.

Общая задача о смещении
-
Число
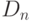 перестановок из
перестановок из  элементов, при которых ни один элемент не остается в первоначальном положении:
элементов, при которых ни один элемент не остается в первоначальном положении:![D_n=P_n-C_n^1 P_{n-1}+C_n^2 P_{n-2}-…+(-1)^n C_n^n P_0 = n! \left[1-\frac{1}{1!}+ \frac{1}{2!}-…+ \frac{(-1)^n}{n!} \right]](/sites/default/files/tex_cache/44ab8bab4f0388120d41f48b4abb871b.png)
( 1) -
Число перестановок ,в которых ровно
 элементов остаются на месте ,а остальные
элементов остаются на месте ,а остальные  меняют свое положение выражается формулой
меняют свое положение выражается формулой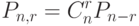
( 2) В самом деле сначала нужно выбрать какие именно
 элементов остаются на месте. Это можно сделать
элементов остаются на месте. Это можно сделать 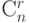 способами , а остальные переставлять.
Это можно сделать
способами , а остальные переставлять.
Это можно сделать 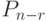 способами. По правилу произведения получаем
способами. По правилу произведения получаем  .
. -
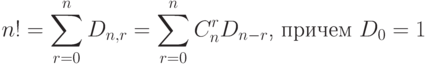
( 3) -
Число перестановок из
 элементов, при которых данные
элементов, при которых данные  элементов смещены (остальные могут быть смещены, а могут оставаться на своих местах), выражается формулой.
элементов смещены (остальные могут быть смещены, а могут оставаться на своих местах), выражается формулой.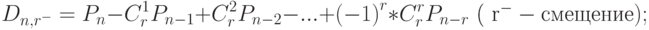
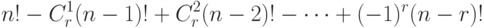
( 4)
Смещение пар
Задача 2. По пустыне идет караван из 9 верблюдов. За много дней путешествий надоедает видеть впереди себя одного и того же верблюда.
Сколькими способами можно переставить верблюдов так, чтобы впереди каждого шел другой, чем раньше?
Для решения задач перенумеруем верблюдов в первоначальном порядке от конца каравана к его началу числами: 1, 2, 3, 4, 5, 6, 7, 8, 9. Нам нужно найти все перестановки из чисел, в которых не встречаются пары 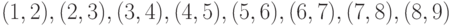 .
.
Используем формулу включения-исключения.
-
Сосчитаем во скольких перестановках входит пара
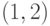 . Можно предположить в этих перестановках пару за один элемент. Следовательно, всего 8 элементов, и число перестановок из 8-ми элементов, содержащих пару
. Можно предположить в этих перестановках пару за один элемент. Следовательно, всего 8 элементов, и число перестановок из 8-ми элементов, содержащих пару 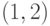 равно
равно  .
.Тот же результат получаем для всех 8-ми пар.
- Рассмотрим перестановки, содержащие данные две пары. В этом случае объединяем элементы, входящие в две пары:
- если обе пары содержат один и тот же элемент, например
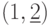 и
и  , то всего
, то всего  перестановок.
перестановок. - если в парах элементы разные , например
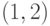 и
и  .
.
- если обе пары содержат один и тот же элемент, например
В обоих случаях получаем 7 новых элементов, которые можно переставлять друг с другом  способами. А две пары из 8 можно выбрать
способами. А две пары из 8 можно выбрать  способами. Совершенно так же доказывается ,что количество перестановок , содержащих
способами. Совершенно так же доказывается ,что количество перестановок , содержащих  пар равно
пар равно 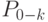 . При этом
. При этом  пар можно выбрать
пар можно выбрать  способами. По формуле включения-исключения получаем, что количество перестановок, не содержащих ни одной из заданных пар, равно:
способами. По формуле включения-исключения получаем, что количество перестановок, не содержащих ни одной из заданных пар, равно:
![\begin{array}{l}
N^{(n)}=P_9 - C_8^1 P_8 + C_8^2 P_7 - C_8^3 P_6 + C_8^4 P_5 - C_8^5 P_4 + C_8^6 P_3 - C_8^7 P_2 + C_8^8 P_1= \\
8!\left[9 - \frac{8}{1!}+ \frac{7}{2!}- \frac{6}{3!}+ \frac{5}{4!}- \frac{4}{5!}+ \frac{3}{6!}- \frac{2}{7!}+ \frac{8}{1!} \right] = 148329.\\
\end{array}](/sites/default/files/tex_cache/5eac957e3a4b82c8d3b4f7cfb4cfdb84.png)
-
Аналогично доказывается ,что количество перестановок из
 чисел
чисел  не содержащих ни одной из пар
не содержащих ни одной из пар 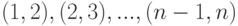 выражается формулой:
выражается формулой:
( 5) -
Совершенно так же доказывается ,что количество перестановок из
 элементов, в которые не входят заданные
элементов, в которые не входят заданные 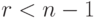 пар, равно
пар, равно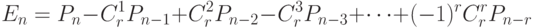
( 6) - если
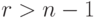 , то
, то![E_n=P_n-C_{n-1}^1 P_{n-1}+ C_{n-1}^2 P_{n-2}-…-(-1)^k C_n^k P_{n-k}+…+(-1)^{n-1} C_{n-1}^{n-1} P_1=\\
= n! \left[1-\frac{1}{1!}+ \frac{1}{2!} - … + \frac{(-1)^{n-1}}{(n-1)!} \right] = n*D_{n-1}](/sites/default/files/tex_cache/c0ad44b933eb544c72345ad01157efa4.png)
( 7)
Задача 3. "Карусель"
На карусели катаются  ребят. Они решили пересесть таким образом, чтобы впереди каждого оказался другой, чем был раньше. Сколькими способами они могут это сделать?
ребят. Они решили пересесть таким образом, чтобы впереди каждого оказался другой, чем был раньше. Сколькими способами они могут это сделать?
Эта задача похожа на предыдущую, но теперь число запрещенных пар равно 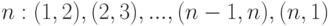 . Кроме того, перестановки, получаемые друг из друга пересадкой по кругу, считать не будем. Поэтому из
. Кроме того, перестановки, получаемые друг из друга пересадкой по кругу, считать не будем. Поэтому из  элементов , можно сделать
элементов , можно сделать 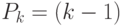 ! существенно различных перестановок .
! существенно различных перестановок .
В этой задаче могут быть все  пар, так как
пар, так как  !, а перестановок всего
!, а перестановок всего 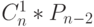 . По формуле включения-исключения получаем:
. По формуле включения-исключения получаем:
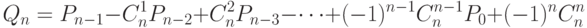 |
( 8) |
По сравнению с формулой (5) мы берем  пар, а не
пар, а не 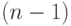 , но так как следует учитывать вращение, то
, но так как следует учитывать вращение, то 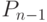 ,а не
,а не 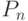 . Формула смещения в общем виде:
. Формула смещения в общем виде:
 |
( 5) |

