Правила суммы и произведений

Формула включения-исключения

Разобранные примеры позволяют сформулировать общий закон.

Пусть имеется предметов , некоторые из которых обладают свойствами .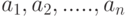

Обозначим через количество предметов , обладающих свойствами .(и, может быть , еще некоторыми из других свойств ).

Если надо подчеркнуть , что берутся предметы , не обладающие некоторым свойством, то это свойство пишется со штрихами. Например: 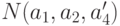- количество предметов, обладающих свойством 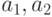, но не обладающих свойством .

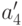В самом простом случае при одном свойств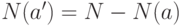е , где - общее число элементов, формула очевидна.

Если имеются два свойства 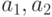, то

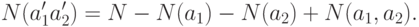
Действительно , каждый элемент , обладающий свойствами и одновременно вычитается дважды, следовательно, к этой разности нужно добавить .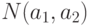

Обобщением этого правила является следующий принцип включения-исключения:

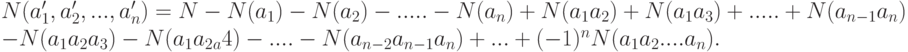
Задача.

Сколько чисел в первой сотне которые , не делятся нацело ни на 2, ни на 3, ни на 5?

Эта задача решается с помощью формулы включения-исключения.

Введем обозначения:

- свойство чисел делиться на2;

- свойство чисел делиться на3;

- свойства чисел делиться на5;

Тогда, 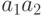означает ,что число делится на 6, 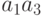означает ,что число делится на 10, означает ,что число делится на 15, наконец, означает, что число делится на 30.

По формуле включения-исключения имеем

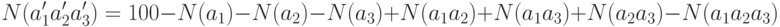
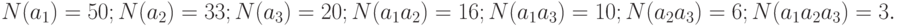
Таким образом, 26 чисел из 100 не делятся ни на 2,ни на 3, ни на 5.

Аналогичная задача. Сколько чисел не делятся нацело на 2, 3, 5, из первой тысячи? Эти задачи в математике были сформулированы математиком Эратосфеном . В математике Эратосфена интересовал как раз вопрос о том , как найти все простые числа среди натуральных чисел от до .

Задача "В чем ошибка ?".

Староста одной группы дал следующие сведения о студентах:

в группе учатся 45 студентов, в том числе 25 юношей. 30 студентов учатся на хорошо и отлично, в том числе 16 юношей. Спортом занимаются 28 студентов, в том числе 18 юношей и 17 студентов, которые учатся на хорошо и отлично. 15 юношей учатся на 4 и 5 и занимаются спортом.

Обозначим:

- принадлежность к мужскому полу ; - хорошую успеваемость ; - увлечение спортом.

Найдем 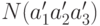- ? то есть число девочек , которое учатся на 3 и ниже и не занимаются спортом.

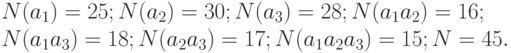
Но, отрицательного ответа не может быть, следовательно, в сведениях есть ошибка.