|
Непонятно почему в примере - отношение t НЕ транзитивно, ведь пары (2,4) и (4, 6) влекут (2, 6) и эта пара имеет общий делитель 2.? |
Комбинаторика
Упорядоченные подмножества. Размещения
Упорядоченные  -элементные подмножества множества из
-элементные подмножества множества из  элементов называются размещениями из
элементов называются размещениями из  элементов по
элементов по  .
.
Различные размещения из  по
по  отличаются компонентами либо их порядком. Общее число размещений без повторений из
отличаются компонентами либо их порядком. Общее число размещений без повторений из  элементов по
элементов по  обозначаются
обозначаются 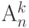 и равно
и равно
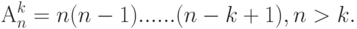
Так как повторение элементов не допускается, то всегда  . Будем считать, что при
. Будем считать, что при 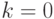 имеем одно размещение (элементы вообще не выбираются), т. е. положим
имеем одно размещение (элементы вообще не выбираются), т. е. положим 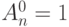 .
.
Размещение  элементов можно представить себе как заполнение некоторых
элементов можно представить себе как заполнение некоторых  позиций элементами заданного множества. При этом 1-ю позицию можно заполнить
позиций элементами заданного множества. При этом 1-ю позицию можно заполнить  различными способами. После того как 1-я позиция заполнена, элемент для заполнения 2-й позиции можно выбрать
различными способами. После того как 1-я позиция заполнена, элемент для заполнения 2-й позиции можно выбрать 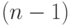 способами. Если этот процесс продолжить, то после заполнения позиций с 1-й по
способами. Если этот процесс продолжить, то после заполнения позиций с 1-й по  -ю будет иметься
-ю будет иметься  способов заполнения последней
способов заполнения последней  -й позиции. Перемножая эти цифры, мы получаем формулу.
-й позиции. Перемножая эти цифры, мы получаем формулу.
В частном случае, когда  , имеем
, имеем
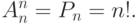
Пример. Пусть дано множество из четырех элементов  . Какие различные размещения по два элемента можно составить и сколько их, т. е.
. Какие различные размещения по два элемента можно составить и сколько их, т. е. 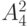 ?
?
Задача. Студенту необходимо сдать 4 экзамена за 8 дней. Сколькими способами можно это сделать, если в один день сдавать не более одного экзамена?
Искомое число способов равно числу четырехэлементных упорядоченных подмножеств (дни сдачи экзаменов) множества из 8 элементов:
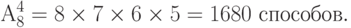
Размещения с повторением
Любой упорядоченный набор  элементов множества, состоящего из
элементов множества, состоящего из  элементов называется размещением с повторением
элементов называется размещением с повторением 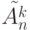 из
из  элементов по
элементов по  . Число различных размещений с повторениями есть
. Число различных размещений с повторениями есть
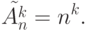
Пример. Для множества  предыдущего примера число различных двухэлементных размещений с повторениями
предыдущего примера число различных двухэлементных размещений с повторениями 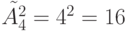 . В множество
. В множество  к тому, что записано, добавляются следующие элементы
к тому, что записано, добавляются следующие элементы  .
.
Задача. Все буквы, цифры, знаки в ЭВМ кодируются двоичными последовательностями определенной длины, компоненты которой равны 0 или 1.
Например:
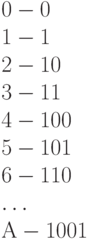
Максимальное число символов (букв, цифр, ......), которые могут быть представлены с помощью  двоичных символов (
двоичных символов (  бит) равно числу размещений с повторениями q элементов из множества, содержащего два различных элемента
бит) равно числу размещений с повторениями q элементов из множества, содержащего два различных элемента 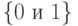 , т. е.
, т. е. 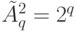 .
.
Обратная задача. Сколько различных чисел (знаков) может быть записано двоичными словами длиной 4, 8 , 16:

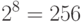
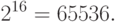
Или имеется алфавит из 64 слов. Сколько необходимо разрядов, чтобы закодировать в двоичной системе.
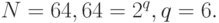

 .
.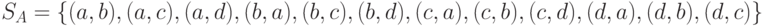 .
.