|
В лекции 3 часть номер 2 приведён пример нахождения транзитивного замыкания по матрице смежности. Из примера для обратного транзитивного замыкания видно, что путь для достижения вершины х6 в вершину х3 равен 3, а не 2, как показано в табличном примере. Мне кажется, что в лекции ошибка. |
Типы графов
Теорема о двудольности
Граф G = (X, A) является двудольным тогда и только тогда, когда он не содержит циклов нечетной длины.
Доказательство
1. Необходимость. Поскольку множество X разбивается на две части Xа
и Xb
, то 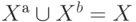 и
и 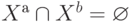 .
.
Пусть существует цикл нечетной длины хi1
, хi2, ...,хi q , хi1
. Без потери общности допустим, что 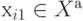 . Согласно определению одна из двух следующих друг за другом вершин этого цикла должна принадлежать множеству Xа
, а другая – множеству Xb
, тогда имеем:
. Согласно определению одна из двух следующих друг за другом вершин этого цикла должна принадлежать множеству Xа
, а другая – множеству Xb
, тогда имеем: 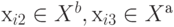 и т. д. Следовательно,
и т. д. Следовательно, 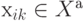 , если k – нечетное, и
, если k – нечетное, и  , если k – четное.
, если k – четное.
Мы предположили, что длина цикла нечетная. Поэтому из соотношения  следует, что
следует, что 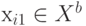 . Это противоречит исходному условию, поскольку
. Это противоречит исходному условию, поскольку 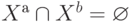 и вершина не может принадлежать одновременно как Xa
, так и Xb
.
и вершина не может принадлежать одновременно как Xa
, так и Xb
.
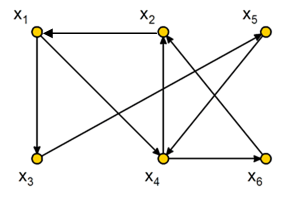
Для большей ясности можно рассмотреть цикл нечетной длины для графа, изображенного на рис. 5.6:
х1---х3--- х5--- х4--- х2--- х1
Xа Xb Xа Xb Xа Xb .
Поочередно помечая вершины, мы видим противоречие: вершина 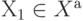 и согласно определению должна принадлежать Xb, следовательно, рассматриваемый граф не является двудольным.
и согласно определению должна принадлежать Xb, следовательно, рассматриваемый граф не является двудольным.
2. Достаточность. Предположим, что в графе G не существует цикла нечетной длины. Выберем одну из вершин графа, например, хi, и пометим ее "+". Выполним итерационную процедуру.
Берем уже помеченную вершину хi и помечаем все вершины из множества Г+1(хi) знаком, противоположным тому, который присвоен вершине хi .
Будем продолжать эту операцию до тех пор, пока не будет сделано следующее:
1) все вершины не будут помечены, а знаки, приписанные им, согласованы (иными словами, любые две вершины, соединенные ребром, помечены противоположными знаками);
2) для каждой помеченной вершины хi все вершины из множества Г+1(хi) помечены, но существуют другие, еще не помеченные вершины;
3) некоторая вершина, например хik , которая была уже помечена каким-то знаком ( "+" или "–" ), может быть помечена теперь (со стороны другой вершины) знаком, противоположным приписанному вершине хik .
В случае 1 все вершины , помеченные знаком "+", отнесем к множеству Xa , а помеченные знаком "–" – к множеству Xb . Поскольку все ребра соединяют вершины, помеченные противополож-ными знаками, то граф является двудольным.
Рассмотрим граф на рис. 5.5б. Пометим знаком "+", например, вершину х1 . Найдем отображение Г+(х1) = { х4, х5 }. Вершины х4 и х5 пометим знаком "–". Отображение Г+(х4, х5) = = { х2, х3 }, помечаем вершины х2 и х3 знаком "+". Г+(х2, х3) = = { х4, х5, х6 }. Оставшуюся непомеченной вершину х6 помечаем знаком "–". Таким образом, получили два подмножества вершин Xa = { х1, х2, х3 } и Xb = { х4, х5, х6 } и показали, что рассматриваемый граф является двудольным.
Случай 2 означает, что между помеченной и непомеченной вершинами не существует дуги. Перейдем к неориентированному графу и повторим процедуру пометок знаками "+" и "–". Если остались непомеченные вершины, то это означает, что граф распадается на две или больше частей, и каждая из них может тогда рассматриваться отдельно. Итак, в конце приходим к случаю 1.
В графе на
рис.
5.5в, пометки были начаты знаком "+" с вершины х 2
. Г+(х2) = { х4 }. Вершина х4
помечается знаком "–". Г+(х4) = { х3 }. Вершина х3
помечается знаком "+". 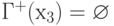 .
.
В графе остались непомеченные вершины, но если перейти к неориентированному двойнику этого графа, то процедура пометок легко выполняется и множество вершин разбивается на два подмножества Хa= { х1, х2, х3 } и Хb= { х4, х5, х6 }, тем самым исходный граф является двудольным.
В случае 3 вершина хik должна быть помечена знаком "+" на некотором маршруте (например, М1), состоящем из вершин хi1, хi2, ..., хik ; причем знаки "+" и "–", приписываемые этим вершинам при движении по маршруту М1, должны образовывать чередующуюся последовательность. Например, для графа на рис. 5.6 маршрут М1 можно выбрать таким:
М1: х1 -> х3 -> х5 -> х4 -> х2.
"+" "-" "+" "-" "+"
Аналогично знаком "-" вершина хik помечается вдоль некоторого маршрута М2 . Например,
М2: х1 -> х4 -> х6 -> х2.
"+" "-" "+" "-"
Пусть x* – предпоследняя (последней является хik ) общая вершина маршрутов М1 и М2 . Если вершина x* помечена знаком "+", то участок от x* до хik маршрута М1 должен быть четным, а участок от x* до хik маршрута М2 должен быть нечетным. Если же вер-шина x* помечена знаком "-", то участок маршрута М1 будет нечетным, а маршрута М2 – четным. Следовательно, цикл, состоящий из участка маршрута М1 , от x* до хik , и соответствующего участка маршрута М2 , от хik до x* , имеет нечетную длину. Это противоречит предположению, что граф не содержит циклов нечетной длины, и, значит, случай 3 невозможен.
В рассматриваемом примере x* = х4 . В маршруте М1 длина участка от х4 до х2 равна 1, а в маршруте М2 длина участка от х4 до х2 равна 2, что в сумме составляет нечетное число, следовательно, граф содержит цикл нечетной длины и не является двудольным.