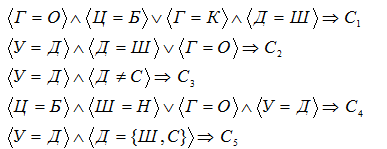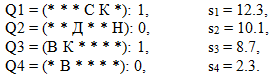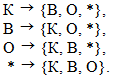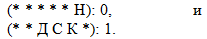| Россия, Волгоградская область |
Машинное обучение
7.2. Мичиганский подход
Здесь системы классификации используют структуру, в которой популяция правил закодирована в строки битов и развивается и совершенствуется на основе меняющихся входных данных, поступающих из внешней среды [1,2]. Система "обучается" на представленных входных данных по методу обучения с учителем, где для каждого набора входных данных известны правильные значения выходов. Правила в системе классификации формируют популяцию из особей, развивающихся во времени. Система классификации, представленная на рис. 7.1 состоит из следующих компонентов:
- датчик и исполнительный элемент;
- система обмена сообщениями (входные, выходные и внутренние списки сообщения);
- система правил (популяция классификаторов);
- система оценки эффективности и отбора правил ("бригадный алгоритм");
- генетический алгоритм (репродукция классификаторов).
Среда (внешнее окружение системы классификации) посылает сообщение, которое принимается датчиками системы классификации и помещается во входной список сообщений. Датчики декодируют сообщение в одно или более (декодированных) сообщений и размещают его во внутренний список сообщений. Эти сообщения активизируют классификаторы. Наиболее сильные из активизированных классификаторов размещают сообщения в списке внутренних сообщений. Эти новые сообщения могут активизировать другие классификаторы, или послать некоторые сообщения в выходной список сообщений. В последнем случае, исполнительные элементы системы классификации кодируют их в выходные сообщения, которые возвращаются во внешнюю среду. Среда оценивает действие системы посредством обратной связи с помощью "бригадного алгоритма", который модифицирует "силу" классификаторов [1,2].
Далее рассмотрим более подробно некоторые из этих действий. Сначала определим некоторые базовые понятия. Каждый классификатор состоит из двух частей: 1-я часть условие, и 2-я сообщение. "Условная часть" правила представляет собой конечную строку символов из некоторого алфавита. Здесь алфавит включает "неопределенный" символ "*". Часть, представляющая сообщение, является конечной строкой из символов того же самого алфавита, кроме символа "*".
Далее мы будем использовать (шуточный) пример классификации роботов [5]. Пусть каждый робот описывается шестью атрибутами, которые могут принимать следующие значения, представленные в таблице 7.1.
| Атрибуты | Значение Атрибутов: |
|---|---|
| Форма Головы | Округлая, Квадратная, Восьмиугольная |
| Форма Тела | Округлая, Квадратная, Восьмиугольная |
| Улыбка | Да, Нет |
| Держит в руках | Сабля, Шарик, Флаг |
| Цвет куртки | Белый, Жёлтый, Зелёный, Синий, Красный |
| Шарф | Да, Нет |
Здесь жирные буквы используются для идентификации атрибутов и их значений. Например, (Ц=Ж) означает "Цвет_Куртки = Жёлтый". Приведем примеры описаний концепций 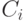 (классов или видов) роботов:
(классов или видов) роботов:
-
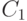 - голова округлая и куртка белая, или голова квадратная и держит шарик;
- голова округлая и куртка белая, или голова квадратная и держит шарик; -
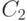 - улыбается и держит шарик, или голова округлая;
- улыбается и держит шарик, или голова округлая; -
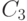 - улыбается и не держит саблю;
- улыбается и не держит саблю; -
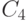 - куртка белая и не носит шарф, или голова круглая и улыбается;
- куртка белая и не носит шарф, или голова круглая и улыбается; -
 - улыбается и держит шарик или саблю.
- улыбается и держит шарик или саблю.
Здесь каждая концепция 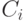 описана в терминах этих шести атрибутов и их значений. Формальное описание концепций представлено на языке
описана в терминах этих шести атрибутов и их значений. Формальное описание концепций представлено на языке  (упрощенная версия распространенного языка Variable Valued Logic Systems), описывающем входные события в пространстве атрибутов.
(упрощенная версия распространенного языка Variable Valued Logic Systems), описывающем входные события в пространстве атрибутов.
Описание концепции  представляется в виде дизъюнкции комплексов
представляется в виде дизъюнкции комплексов

При этом каждый комплекс 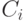 выражен посредством конъюнкции селекторов, которые являются триплетами (например, (Ц=Ж) для "Цвет куртки = Желтый").
выражен посредством конъюнкции селекторов, которые являются триплетами (например, (Ц=Ж) для "Цвет куртки = Желтый").
Концепции  могут быть выражены следующим образом:
могут быть выражены следующим образом:
Каждому классификатору приписывается "сила", характеризующая его "важность"."Сила" важна в процессе "торговли", где классификаторы конкурируют за право послать сообщения. Мы можем представить решающее правило с помощью одного или более классификаторов. Каждый классификатор имеет следующую форму  , где
, где 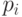 обозначает значение
обозначает значение  -го атрибута
-го атрибута  для областей значений, описанных выше.
для областей значений, описанных выше.
Например, классификатор, (О * * * Б *):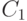 представляет следующее правило: "Если голова Округлая и куртка Белая, то робот соответствует концепции
представляет следующее правило: "Если голова Округлая и куртка Белая, то робот соответствует концепции 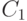 ". Здесь концепция фактически соответствует классу, к которому принадлежит робот.
". Здесь концепция фактически соответствует классу, к которому принадлежит робот.
Чтобы упростить пример, предположим, что система обучается единственной концепции 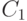 . Но рассматриваемый метод может быть легко обобщен для обработки множественных концепций. В случае одной концепции каждый классификатор имеет следующую форму
. Но рассматриваемый метод может быть легко обобщен для обработки множественных концепций. В случае одной концепции каждый классификатор имеет следующую форму  , где
, где  (принадлежность к концепции
(принадлежность к концепции 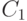 ) или
) или 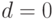 (в противном случае).
(в противном случае).
Предположим, что на некоторой стадии процесса обучения в системе имеется небольшая (случайная) популяция классификаторов  . При этом каждый классификатор имеет свою силу
. При этом каждый классификатор имеет свою силу  . Пусть для определенности в нашем примере на текущий момент присутствуют следующие классификаторы:
. Пусть для определенности в нашем примере на текущий момент присутствуют следующие классификаторы:
Предположим далее, что из внешней среды поступает новое входное сообщение  (ООДСБН). Оно представляет описание одного робота с округлой головой (О), округлым телом (О), который улыбается (Д), держит саблю (С) и одет в белую (Б) куртку без шарфа (Н). Очевидно, этот робот вписывается (соответствует) в концепцию
(ООДСБН). Оно представляет описание одного робота с округлой головой (О), округлым телом (О), который улыбается (Д), держит саблю (С) и одет в белую (Б) куртку без шарфа (Н). Очевидно, этот робот вписывается (соответствует) в концепцию 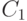 из-за его округлой головы и белой куртки.
из-за его округлой головы и белой куртки.
Анализ показывает, что это сообщение активизирует три классификатора:  . Эти классификаторы "торгуются": предложение каждого классификатора в торге пропорционально его силе
. Эти классификаторы "торгуются": предложение каждого классификатора в торге пропорционально его силе  . Самый сильный классификатор
. Самый сильный классификатор  выигрывает и посылает свое сообщение. Так как сообщение дает правильную классификацию, этот классификатор получает премию
выигрывает и посылает свое сообщение. Так как сообщение дает правильную классификацию, этот классификатор получает премию  . Тогда сила классификатора становится равной:
. Тогда сила классификатора становится равной:

Если бы сообщение дало неправильный ответ, "премия" r была бы отрицательна. Конкретно для коэффициентов  и
и  , новая сила классификатора
, новая сила классификатора  составляет
составляет  .
.
Одним из основных параметров системы классификаторов является период ГА  , который определяет число временных шагов (число циклов описанных выше) между запросами ГА. Конечно,
, который определяет число временных шагов (число циклов описанных выше) между запросами ГА. Конечно,  может быть константой, генерируемой произвольно (со средним значением, равным
может быть константой, генерируемой произвольно (со средним значением, равным  ), или вообще не определенно, и этот выбор может быть сделан, исходя из характеристик работы системы. Так или иначе, предположим, что настало время для применения генетического алгоритма в классификации.
), или вообще не определенно, и этот выбор может быть сделан, исходя из характеристик работы системы. Так или иначе, предположим, что настало время для применения генетического алгоритма в классификации.
В данном подходе сила классификаторов рассматривается в качестве значений фитнесс-функции и при выборе родителей здесь используется пропорциональный отбор (колесо рулетки).
Далее используются стандартные генетические операторы: репродукция, мутация и кроссинговер. Однако их необходимо несколько модифицировать. Рассмотрим, например, первый атрибут. Его областью (форма головы) является {О, К, В, *}. Поэтому, при мутации, мы заменяем изменяемое значение на любое из трех других значений (с равной вероятностью):
После выполнения оператора мутации сила потомка обычно остаётся такой же, как и у родительской особи. Оператор кроссинговера в данном случае не требует никакой модификации (то есть применяется классический ОК). Этому способствует также тот факт, что все классификаторы имеют равную длину. Далее, применив кроссинговер к двум родителям, например,  и
и  , получим:
, получим:
Случайным образом генерируется номер позиции для кроссинговера (например, как показано, после третьего символа), и получаем следующий результат (особи - потомки):
При кроссинговере сила полученных классификаторов определяется как среднее значение (возможно взвешенное) от значений силы родителей.
Далее процесс обучения продолжается: принимаются новые положительные и отрицательные сообщения из внешней среды, производится "торг" и модифицируются "силы" классификаторов. Можно показать, что в конечном счете популяция классификаторов сходится к некоторому числу сильных особей (классификаторов), например,
Приведенный пример является, конечно, искусственным и предназначен для иллюстрации основных принципов обучения, используемых в Мичиганском подходе. Следует отметить, однако, что при "торге" в примере использовалась самая простая система оценок эффективности классификаторов. Существуют и более сложные (и эффективные) методы оценки классификаторов.