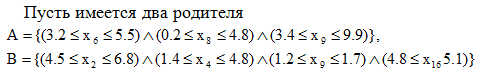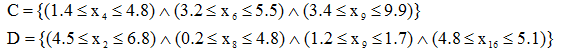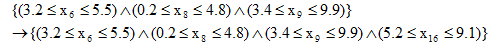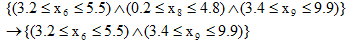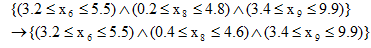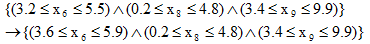Машинное обучение

7.4. Применение ГА в задачах прогнозирования

В [4,9] исследованы возможности применения ГА к некоторым проблемам анализа данных и прогнозирования. Общая проблема может быть сформулирована в следующем виде: серия наблюдений некоторого процесса имеет вид 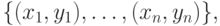, где 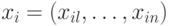– независимые и – соответственно зависимые переменные. В прогнозировании, например течения некоторого заболевания, независимые переменные могут представлять характеристики состояния больного в настоящем или прошлом (пусть для определенности, факторы риска атеротромбогенного инсульта). Зависимая переменная соответствует некоторым признакам будущего состояния здоровья или рекомендациям по лечению (например: 1) дальнейшее наблюдение врача; 2) медикаментозное лечение; 3) рекомендация на операцию - удаление атеросклеротической бляшки).

В качестве зависимой переменной используется прогнозируемая величина, например, возможный исход заболевания. В качестве зависимой может быть и векторная переменная, содержащая несколько компонент.

Таким образом, множество данных представляет набор аналогичных входных воздействий (влияющих факторов), произошедших в прошлом, в сочетании со значениями прогнозируемой величины, которые были получены в результате действия влияющих факторов.

При прогнозировании в данном методе в качестве особи используется некоторое условие на независимые переменные. В конечном счете, необходимо найти такое множество условий (популяцию), которое дает хорошее предсказание для зависимых переменных. Например, условие (особь) может иметь следующий вид:

где представляет логический оператор "И". Такое условие определяет некоторое подмножество из множества данных процесса. Фактически это условие является более формализованной формой представления правил-продукций, рассмотренных выше. Переменные здесь соответствуют зависимым переменным, например, факторам риска. Таким образом, популяцию составляют множество условий на независимые переменные.

При данном подходе целью является выбор с помощью генетических алгоритмов таких наблюдений из множества данных, которые имеют сходные тенденции изменений независимых переменных, и близкие значения зависимых переменных. Эти зависимые переменные собственно и определяют прогнозируемые значения. Условие также должно однозначно удовлетворять и такому наблюдению, для которого выполняется прогноз. Таким образом, генетические алгоритмы выбирают из фактов, которые уже состоялись в прошлом, те, которые имеют достаточно много общего с фактом, который присутствует в настоящем. Это соответствует гипотезе локальной компактности. Можно предположить, что если из похожих фактов можно сделать близкие выводы, подобный же вывод можно сделать и из текущего наблюдения на основании гипотезы линейных зависимостей, допустим, простой операцией усреднения зависимой(ых) переменной(ых).

Фитнесс-функция для каждой особи (условия) вычисляется на основании всех данных наблюдений в обучающем множестве, которые удовлетворяют этому условию. Следует отметить, что с одной стороны, чем больше данных, тем лучше, но с другой, большое количество данных неизбежно приводит к большому разнообразию во множестве зависимых переменных, на основании которых, собственно, и строится прогноз.

В данном подходе обычно используется следующая фитнесс-функция:

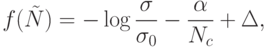
где:

• -стандартное отклонение (дисперсия) для зависимых переменных из множества данных, удовлетворяющих заданному условию ;
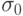• -стандартное отклонение (дисперсия) для зависимых переменных всего множества обучающих данных;
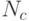• количество наблюдений, которые удовлетворяют данному ограничению ;
• и - константы.

Как видно из приведенного выражения, фитнесс-функция имеет три составляющие (слагаемых).

Первая составляющая оценивает разброс данных, отобранных данным условием. Чем ближе между собой данные в пространстве независимых переменных, тем меньше дисперсия для условия , и тем большее значение имеет первая составляющая.

Вторая составляющая оценивает размер выборки, которую представляет данное условие. Чем большее число наблюдений удовлетворяет данному условию, тем меньше значение этой составляющей и тем больше значение целевой функции. Таким образом, вторую составляющую можно назвать "штрафом для условий с бедной статистикой". Для того чтобы вторая составляющая была соизмерима с первой, введен масштабный коэффициент .

Третья составляющая введена для того, чтобы существовала возможность регулирования величины фитнесс-функции относительно нуля.

Представление особи и инициализация популяции

Каждая особь популяции представляется линейной структурой (унарным деревом). Каждый узел данного дерева имеет атрибуты: "имя переменной", "левая граница", "правая граница", "потомок". Таким образом, каждый узел определяет диапазон для какой-либо одной переменной. К нему может быть присоединен (или нет) узел–потомок. Таким образом, особь представляется унарным деревом, которое имеет максимум узлов (которые соответствует независимым переменным), и для каждой из них определен диапазон изменения (верхняя и нижняя граница).

Отбор особей для размножения.

Используются стандартные оператор репродукции, например, "колесо рулетки".

Оператор кроссинговера.

В данном методе представления особи чаще всего применяется версия оператора кроссинговера, основанная на равновероятном случайном выборе узлов от каждого родителей. Каждый ген (ограничение на значения переменной) потомка наследуется у одного из родителей с вероятностью .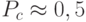

Оператор мутации.

Для данного представления особей возможны следующие операторы мутации:

1. Добавление ограничения, которое добавляет в дерево новое ограничение.
2. Удаление ограничения, которое удаляет один случайный узел из дерева.
3. Расширение или сужение диапазона изменения некоторой переменной.
4. Сдвиг диапазона изменения переменной вверх или вниз.
5. Полная перестройка дерева, при которой особь полностью удаляется и вместо нее заново случайным образом генерируется новая особь.

Использование алгоритмов такого вида по сравнению со стандартными имеет следующие преимущества:

• вместо того чтобы искать функциональную зависимость прогнозируемой величины от набора влияющих факторов, производится отбор аналогичных ситуаций, выбранных из множества наблюдений. Поскольку функциональная зависимость может не быть постоянной, а также зачастую весьма сложно выражается, данное преимущество весьма существенно.
• может использоваться сколь угодно большое количество влияющих переменных, а не только прошлые значения из временного ряда. Это снижает недостаток малой длины временного ряда.

Для решения задачи прогнозирования можно использовать стандартный ГА, который приведен в разделе 1.

Отбор особей для размножения

При отборе особей для размножения обычно используется стандартный оператор репродукции – "колесо рулетки", который реализует пропорциональный отбор в промежуточную популяцию. При этом особи-родители выбираются случайным образом с вероятностью, зависящей от величины их целевой функции. Для повышения эффективности целевая функция должна плавно увеличиваться от нулевого значения. Для соблюдения этого правила очень важен подбор величины смещения для фитнесс-функции. Построенные в процессе кроссинговера потомки замещают особи, целевая функция которых хуже средней по популяции.

Оператор кроссинговера.

При получении потомства может быть использована следующая версия оператора кроссинговера:

Каждый ген (ограничение на значения переменной) потомка наследуется у одного из родителей с вероятностью 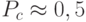. Если у родителей есть узлы с одинаковыми переменными, то они в любом случае помещаются в разные потомки. При этом добавлено правило, которое не позволяет записывать все узлы всех родителей к одному потомку, и не поощряет передачу двух узлов подряд к одному и тому же потомку. Таким образом, возможные потомки для данных родителей могут быть, например, следующие:

Здесь потомок имеет два гена от родителя и один ген от родителя . Потомок имеет один ген от родителя , и три – от родителя .

Оператор мутации

В дополнение к оператору кроссинговера использовались следующие операторы мутации:

1. Добавление ограничения, которое вводит в дерево новое ограничение. Например,
   

   
   
2. Удаление ограничения, которое удаляет один случайный узел из дерева. Например,
   

   
   
3. Расширение или сужение диапазона.
   

   
   
4. Сдвиг диапазона вверх или вниз:
   

   
   
5. Полная перестройка дерева, где особь полностью удаляется, и вместо нее заново случайным образом генерируется новая особь.

Таким образом, глобальный оператор мутации выбирает с равной вероятностью один из этих операторов.

В качестве критерия останова алгоритма обычно используется выполнение условие окончания: повторение лучшего результата заданное количество поколений подряд.

При сокращении промежуточной популяции применяется стратегия элитизма: особь с наилучшим значением целевой функции обязательно переходит в следующее поколение. Для замедления вырождения выборки к одной особи, все особи, которые совпадают с наилучшей, подвергаются мутации.

Определение параметров алгоритма и .

Как указано выше, параметр определяет размер выборки для каждого условия. Чем ниже этот фактор, тем меньшее значение имеет размер выборки, и тем большее значение имеет близость между собой значений зависимых переменных. Параметр определяет величину смещения фитнесс-функции на положительную полуплоскость. Этот параметр должен быть таким, чтобы минимальное значение целевой функции было как можно ближе к 0, но имело положительное значение. Это способствует эффективному функционированию оператора репродукции. Для подбора параметров фитнесс-функции необходимо оценить зависимость точности результата от этих параметров. Например, для различных значений и можно выполнить поиск решений, среди которых найти лучшее. Затем выполнять сравнение лучшего решения с действительным, и найти погрешность результата.

Подбор размера популяции и критерия остановки программы

Аналогично предыдущему пункту производится подбор таких параметров, как размер популяции и количество поколений, в течение которых не улучшается результат (погрешность). Чем меньше размер популяции, тем быстрее выполняется программа, но тем меньше шансов найти оптимальное решение. Напротив, большое число шагов программы до остановки способствует нахождению хорошего решения, но замедляет работу программы.

Подбор вероятности мутации

После выполнения оператора кроссинговера все потомки могут быть подвергнуты мутации с заданной вероятностью. Чем выше эта вероятность, тем больше ГА превращается в алгоритм случайного поиска. Соответственно должно увеличиваться и количество поколений до достижения результата.

Таким образом, в данном разделе рассмотрены возможности применения генетических алгоритмов и генетического программирования к задачам прогнозирования, которые при грамотной реализации дают результаты, сопоставимые с результатами, полученными с помощью многослойных нейронных сетей прямого распространения, но имеют при этом более ясную интерпретацию.

Напомним, что основной проблемой при разработке классических экспертных систем является формирование базы знаний – множества правил-продукций. Для этого привлекаются, как правило, квалифицированные эксперты. Определенную проблему представляет также и обновление знаний в процессе эксплуатации экспертной системы. Преимуществом является, как правило, "прозрачность" правил-продукций и возможность проследить сам процесс вывода – заключения экспертной системы.

В эволюционном подходе предпринята попытка объединить преимущества обоих указанных методов создания экспертных систем – классического и нейросетевого. Фактически этот подход является развитием классического метода построения экспертных систем. Знания хранятся здесь в виде формализованных правил-продукций (почти также как и в обычных экспертных системах). Но здесь есть возможность автоматически строить эти правила-продукции по имеющейся обучающей выборке. Суть данного подхода заключается в том, что из обучающей выборки автоматически выводится множество правил-продукций, которое позволяет с минимальной (в некотором смысле) ошибкой решать поставленную задачу. Для медицинских приложений такой подход является чрезвычайно перспективным – фактически здесь из имеющихся статистических данных по некоторому заболеванию можно фактически автоматически получить методику его диагностирования и прогноза течения заболевания. Это становится возможным благодаря использованию методов эволюционных вычислений.