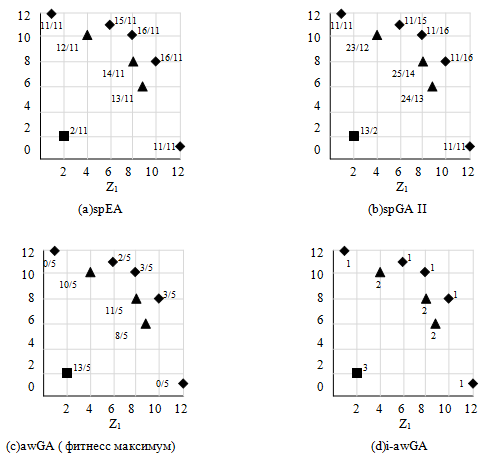
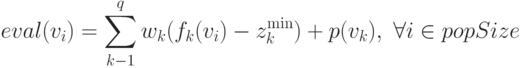| Россия, Волгоградская область |
Генетические алгоритмы многокритериальной оптимизации
5.4.3.Генетический алгоритм с адаптивными весами
В [8] Gen и Cheng предложен подход на основе адаптивных весов, который использует полезную информацию о текущей популяции для коррекции весов для того, чтобы направить поиск в сторону положительной идеальной точки, что показано на рис.5.10.
Здесь на каждой итерации для исследуемых решений определяются в пространстве критериев две экстремальные точки: 1) максимальная экстремальная точка 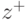 ; 2) минимальная экстремальная точка
; 2) минимальная экстремальная точка 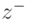 следующим образом:
следующим образом:
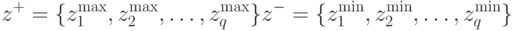
где 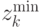 и
и  - минимальное и максимальное значение для
- минимальное и максимальное значение для  -ого критерия в текущей популяции. Пусть
-ого критерия в текущей популяции. Пусть  обозначает множество решений текущей популяции. Тогда определим для данной особи
обозначает множество решений текущей популяции. Тогда определим для данной особи  максимальное и минимальное значение для каждого критерия следующим образом:
максимальное и минимальное значение для каждого критерия следующим образом:
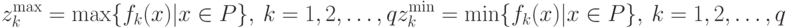
Отметим, что гиперплоскость, определяемая двумя экстремальными точками, является минимальным гиперпараллелограммом, который содержит все текущие решения. Указанные две экстремальные точки обновляются на каждой итерации. При этом адаптивный вес  -ого критерия вычисляется следующим образом
-ого критерия вычисляется следующим образом

Тогда для данной особи  взвешенная целевая функция определяется согласно следующему выражению:
взвешенная целевая функция определяется согласно следующему выражению:
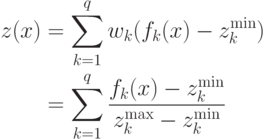
Поскольку экстремальные точки обновляются на каждой итерации, то соответственно обновляются и веса. Последнее уравнение представляет гиперплоскость, которая определяется следующими экстремальными точками во множестве текущих решений:
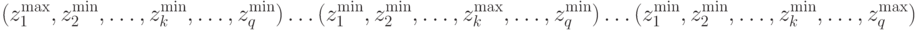
Она задает адаптивную движущуюся линию, которая определяется экстремальными точками 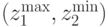 и
и 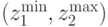 , как показано на рис.5.10. Здесь прямоугольник, определяемый этими экстремальными точками
, как показано на рис.5.10. Здесь прямоугольник, определяемый этими экстремальными точками 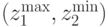 и
и 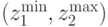 , является минимальным прямоугольником, который содержит все текущие решения. Как показано на рис.5.10 гиперплоскость разделяет пространство критериев
, является минимальным прямоугольником, который содержит все текущие решения. Как показано на рис.5.10 гиперплоскость разделяет пространство критериев  на два подпространства: 1) одно подпространство содержит положительную идеальную точку, обозначаемую,
на два подпространства: 1) одно подпространство содержит положительную идеальную точку, обозначаемую, 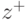 ;2) второе подпространство содержит отрицательную идеальную точку
;2) второе подпространство содержит отрицательную идеальную точку 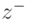 . Все исследуемые решения Парето лежат в пространстве
. Все исследуемые решения Парето лежат в пространстве 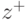 , при этом все точки, лежащие в
, при этом все точки, лежащие в 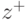 , имеют значения фитнесс-функции большие, чем точки из пространства
, имеют значения фитнесс-функции большие, чем точки из пространства 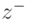 . Поскольку максимальная экстремальная точка аппроксимирует положительную идеальную точку в течение процесса эволюции, гиперплоскость последовательно приближается к положительной идеальной точке. Таким образом, данный метод позволяет корректировать веса целевой функции и направляет поиск решений в сторону положительной идеальной точки. Укрупненный алгоритм метода представлен ниже.
. Поскольку максимальная экстремальная точка аппроксимирует положительную идеальную точку в течение процесса эволюции, гиперплоскость последовательно приближается к положительной идеальной точке. Таким образом, данный метод позволяет корректировать веса целевой функции и направляет поиск решений в сторону положительной идеальной точки. Укрупненный алгоритм метода представлен ниже.
5.4.4. Недоминируемый ГА на основе сортировки
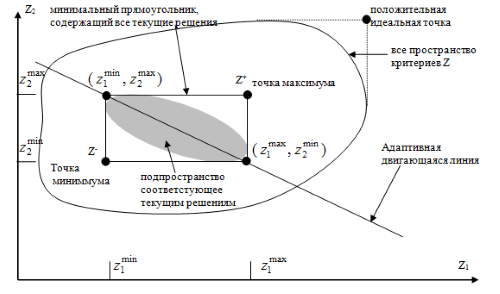
В этом методе (Non-dominated sorting algorithm - nsGA) [9] авторы (Deb) пытаются преодолеть, по крайней мере, три проблемы: вычислительную сложность; трудности элитизма; необходимость определения параметров разделения [10]. Общая схема метода представлена на рис.5.11.
Здесь для каждой особи выполняется ранжирование Парето. При этом, как обычно, первый фронт Парето содержит полностью недоминируемые решения, второй фронт – особи, доминируемые решениями второго фронта, и т.д. Особям первого фронта присваивается ранг 1, второго -2 и т.д. В дополнение рангу для каждой особи выполняется оценка расстояния Кроудинга (crowding)[2].
Расстояние Кроудинга является мерой близости особи к своим соседям. Большое среднее расстояние Кроудинга характеризует разнообразие особей в популяции. Далее выполняется сортировка особей согласно расстоянию Кроудинга – особь с большим расстоянием получает меньший ранг. Турнирный отбор родительских особей выполняется на основе значений ранга и расстояния Кроудинга. Укрупненный алгоритм представлен ниже.
При определении значения фитнесс-функции для двух особей предпочтение отдается точке с низшим рангом или точке, расположенной в области с меньшим числом точек, если обе точки принадлежат одному фронту. Путем комбинирования быстрого недоминируемого подхода с сортировкой, схемы элитизма и метода разделения без параметров авторам удалось получить лучшие результаты для некоторых тестовых задач.
После вычисления значения фитнесс-функции для каждой  -ой особи выполняется специальная процедура отбора. Для двух особей с недоминируемыми рангами
-ой особи выполняется специальная процедура отбора. Для двух особей с недоминируемыми рангами 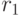 и
и 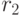 и расстояниями Кроудинга
и расстояниями Кроудинга  и
и 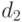 предпочтение отдается решению с низшим (лучшим) рангом согласно следующему правилу
предпочтение отдается решению с низшим (лучшим) рангом согласно следующему правилу 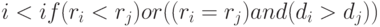
5.4.5 Интерактивный ГА с адаптивными весами
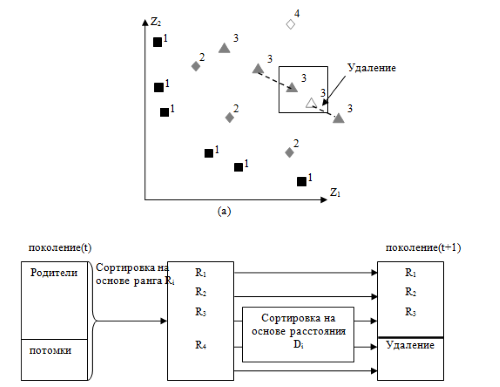
Основная идея ранжирования по Парето основана на четкой классификации недоминируемых и доминируемых решений для каждой особи. Однако порой трудно определить разницу между недоминируемыми и доминируемыми решениями по значениям фитнесс-функции, основанной на ранжировании. Это показано на рис.5.12, где, например, на рис.5.12 с) очевидны различия между доминируемыми и недоминируемыми решениями с координатами 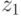 ,
, 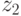 (2.2) и (8,8) соответственно, но значения фитнесс-функции, получаемые по методу awGA, не отличаются для решений 13/5 и 11/5.
(2.2) и (8,8) соответственно, но значения фитнесс-функции, получаемые по методу awGA, не отличаются для решений 13/5 и 11/5.
В отличие от методов определения значений фитнесс-функций, основанных на ранжировании по Парето, в методах определения значений фитнесс-функций, базирующиеся на взвешенной фитнесс-функции, часто легче определить разницу между недоминируемыми и доминируемыми решениями. При этом процесс сортировки становится ненужным, что снижает вычислительные затраты. Для эффективного объединения взвешенных целевых функций в единую целевую функцию необходимо присваивать хорошие значения фитнесс-функции для решений, находящихся близко от фронта Парето.
В [10] предложен улучшенный интерактивный ГА с адаптивными весами, укрупненный алгоритм которого представлен ниже.
Здесь, во-первых, используются две экстремальные точки, определяемые как максимальная экстремальная точка 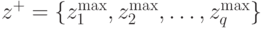 , и минимальная экстремальная точка
, и минимальная экстремальная точка 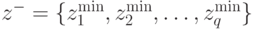 , где
, где 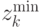 и
и  - минимальное и максимальное значение для
- минимальное и максимальное значение для  -ой цели в текущей популяции. Тогда адаптивный вес для
-ой цели в текущей популяции. Тогда адаптивный вес для  -ой цели вычисляется в соответствии со следующей формулой:
-ой цели вычисляется в соответствии со следующей формулой:

Далее, вычисляется штрафной терм 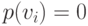 , если
, если 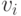 является недоминируемым решением в недоминируемом множестве
является недоминируемым решением в недоминируемом множестве  . Иначе, для доминируемого решения
. Иначе, для доминируемого решения 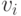 присваивается
присваивается 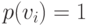 . Наконец, вычисляется значение фитнесс-функции для каждой особи в соответствии с выражением
. Наконец, вычисляется значение фитнесс-функции для каждой особи в соответствии с выражением