| Россия, Волгоградская область |
Введение.Основы генетических алгоритмов
1. Введение в генетические алгоритмы
В этом разделе описывается концепция простого генетического алгоритма (ГА), ориентированного на решение различных оптимизационных задач. Вводятся и содержательно описываются понятия, используемые в теории и приложениях ГА. Приводится фундаментальная теорема ГА и излагается теория схем, составляющие теоретическую базу ГА. Обсуждаются концептуальные вопросы, касающиеся преимуществ и недостатков ГА.
1.1. Простой генетический алгоритм
Основы теории генетических алгоритмов сформулированы Дж. Г.Холландом в основополагающей работе [2] и в дальнейшем были развиты рядом других исследователей. Наиболее известной и часто цитируемой в настоящее время является монография Д.Голдберга [3], где систематически изложены основные результаты и области практического применения ГА.
ГА используют принципы и терминологию, заимствованные у биологической науки – генетики. В ГА каждая особь представляет потенциальное решение некоторой проблемы. В классическом ГА особь кодируется строкой двоичных символов – хромосомой, каждый бит которой называется геном. Множество особей – потенциальных решений составляет популяцию. Поиск оптимального или субоптимального решения проблемы выполняется в процессе эволюции популяции, т.е. последовательного преобразования одного конечного множества решений в другое с помощью генетических операторов репродукции, кроссинговера и мутации. ЭВ используют механизмы естественной эволюции, основанные на следующих принципах:
- Первый принцип основан на концепции выживания сильнейших и естественного отбора по Дарвину, который был сформулирован им в 1859 году в книге "Происхождение видов путем естественного отбора". Согласно Дарвину особи, которые лучше способны решать задачи в своей среде, чаще выживают и чаще размножаются (репродуцируют). В генетических алгоритмах каждая особь представляет собой решение некоторой проблемы. По аналогии с этим принципом особи с лучшими значениями целевой (фитнесс) функции имеют большие шансы выжить и репродуцировать. Формализацию этого принципа, как мы увидим далее, реализует оператор репродукции.
- Второй принцип обусловлен тем фактом, что хромосома потомка состоит из частей, полученных из хромосом родителей. Этот принцип был открыт в 1865 году Г.Менделем. Его формализация дает основу для оператора скрещивания (кроссинговера).
- Третий принцип основан на концепции мутации, открытой в 1900 году де Вре. Первоначально этот термин использовался для описания существенных (резких) изменений свойств потомков и приобретение ими свойств, отсутствующих у родителей. По аналогии с этим принципом генетические алгоритмы используют подобный механизм для резкого изменения свойств потомков и, тем самым, повышают разнообразие (изменчивость) особей в популяции (множестве решений).
Эти три принципа составляют ядро ЭВ. Используя их, популяция (множество решений данной проблемы) эволюционирует от поколения к поколению.
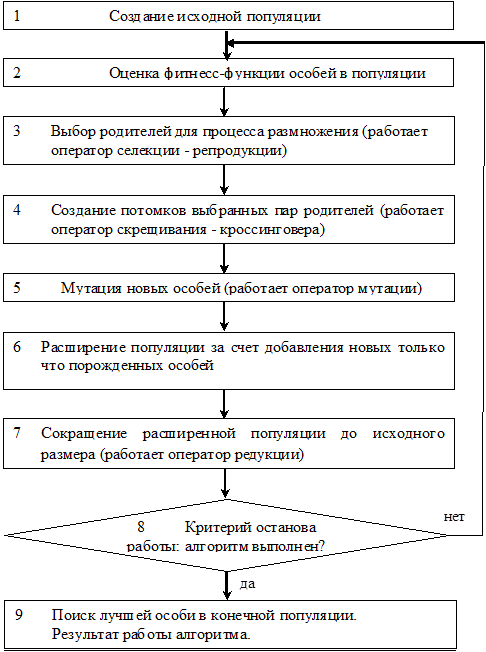
Эволюцию искусственной популяции – поиск множества решений некоторой проблемы, формально можно описать в виде алгоритма, который представлен на рис.1.1.
ГА получает множество параметров оптимизационной проблемы и кодирует их последовательностями конечной длины в некотором конечном алфавите (в простейшем случае в двоичном алфавите "0" и "1").
Предварительно простой ГА случайным образом генерирует начальную популяцию хромосом (стрингов). Затем алгоритм генерирует следующее поколение (популяцию) с помощью трех следующих основных генетических операторов:
- оператора репродукции (ОР);
- оператора скрещивания (кроссинговера, ОК);
- оператора мутации (ОМ).
Генетические алгоритмы – это не просто случайный поиск, они эффективно используют информацию, накопленную в процессе эволюции.
В процессе поиска решения необходимо соблюдать баланс между "эксплуатацией" полученных на текущий момент лучших решений и расширением пространства поиска. Различные методы поиска решают эту проблему по-разному.
Например, градиентные методы практически основаны только на использовании лучших текущих решений, что повышает скорость сходимости с одной стороны, но порождает проблему локальных экстремумов с другой. В полярном подходе случайные методы поиска используют все пространство поиска, но имеют низкую скорость сходимости. В ГА предпринята попытка объединить преимущества этих двух противоположных подходов. При этом операторы репродукции и кроссинговера делают поиск направленным. Широту поиска обеспечивает то, что процесс ведется на множестве решений – популяции и используется оператор мутации.
В отличие от других методов оптимизации ГА оптимизируют различные области пространства решений одновременно и более приспособлены к нахождению новых областей с лучшими значениями целевой функции за счет объединения квазиоптимальных решений из разных популяций.
Упомянутые генетические операторы являются математической формализацией приведенных выше трех основополагающих принципов Ч.Дарвина, Г.Менделя и де Вре естественной эволюции. Каждый из функциональных блоков ГА на рис. 1.1. может быть реализован различными способами. Но сначала на простом примере мы рассмотрим основные моменты классического ГА.