Введение.Основы генетических алгоритмов

1.9. No Free Lunch теорема

Возникает естественный вопрос – существует ли некоторый лучший эволюционный алгоритм, который дает всегда лучшие результаты при решении всевозможных проблем? Например, можно ли выбрать генетические операторы и их параметры так, чтобы алгоритм давал лучшие результаты независимо от решаемой проблемы? К сожалению, ответ отрицательный – такого лучшего эволюционного алгоритма не существует! Это следует из известной No Free Lunch (NFL) теоремы (бесплатных завтраков не бывает), которая доказана относительно недавно, в 1996г.[18,19] и вызвала оживленную дискуссию. Пусть 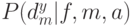- условная вероятность получения частного решения 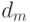после итераций работы алгоритма при целевой функции . В этих терминах Вольперт и Макреди доказали так называемую No Free Lunch (NFL) теорему:

NFL теорема. Для любой пары алгоритмов и имеет место равенство

Таким образом, сумма условных вероятностей посещения в пространстве решений каждой точки 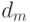одинакова для множества всевозможных целевых функций независимо от используемого алгоритма. Из этого результата непосредственно следует, что при любой мере 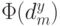производительности (характеристик сложности) алгоритма в среднем для всевозможных целевых функций вероятность 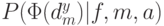не зависит от алгоритма . Другими словами, не существует лучшего алгоритма (эволюционного или любого другого) для решения всех проблем. Если алгоритм выигрывает по своим характеристикам при решении некоторого класса задач, то это неминуемо компенсируется проигрышем (худшими характеристиками) для остальных задач.

Эта теорема вызвала оживленную дискуссию у специалистов по эволюционным вычислениям и некоторое неприятие. Дело в том, что в семидесятых годах были предприняты значительные усилия по поиску лучших значений параметров и генетических операторов ГА. Исследовались различные генетические операторы, значения вероятностей выполнения кроссинговера и мутации, мощности популяции и т.д. Большинство этих исследований апробировалось на сложившихся в каждой проблемной области тестовых задачах. Но из NFL-теоремы следует, что полученные результаты справедливы только на использованных тестовых задачах, а не для произвольных задач. Все усилия найти лучший оператор кроссинговера или мутации, оптимальные значения их параметров при отсутствии ограничений для исследуемого класса задач не имеют смысла!

Каждому эволюционному алгоритму присуще некоторое представление, которое позволяет манипулировать с потенциальными решениями. NFL теорема утверждает, что не существует лучшего эволюционного алгоритма для решения всех проблем.

Для того чтобы разрабатываемый алгоритм решал поставленную задачу лучше, чем случайный поиск (который с точки зрения NFL теоремы является просто другим алгоритмом) необходимо в нем использовать (отразить) структуру (априорные знания) этой проблемы. Из этого следует, что такой алгоритм может не соответствовать структуре другой проблемы (и покажет для нее плохие результаты). Следует отметить, что недостаточно просто указать, что проблема имеет некоторую структуру - такая структура должна соответствовать разрабатываемому алгоритму. Более того, структура должна быть определена. Недостаточно, как это иногда бывает, сказать "Мы имеем дело с реальными проблемами, а не с всевозможными, поэтому NFL теорема не применима". Что значит структура реальной проблемы? Очевидно, что формальное описание такой структуры проблематично. Например, реальные проблемы нашего времени и столетней давности могут сильно отличаться. Следует отметить, что простое сужение области возможных проблем без идентификации соответствия между рассматриваемым множеством проблем и алгоритмом недостаточно для получения преимущества данного метода решения этих проблем по сравнению с другими.

NFL-теорема подтверждает, что разные алгоритмы имеют различную эффективность при решении разных задач. Например, классические методы оптимизации, как правило, более эффективны при решении линейных, квадратичных, строго выпуклых, унимодальных, разделяемых и других специальных классов проблем. С другой стороны, генетические алгоритмы часто успешно решают задачи там, где классические методы не работают – там, где целевые функции терпят разрывы, не дифференцируемы, мультимодальны (имеют много экстремумов), зашумлены и т.п. Обычно их эффективность и устойчивость выше там, где целевые функции имеют сложный (не стандартный) вид, что более характерно для решения реальных практических задач. Конечно, лучшим способом подтверждения эффективности алгоритма является доказательство его сходимости и оценки вычислительной сложности. Но, как правило, это возможно только в случае упрощенной постановки задачи. Другой альтернативой является проверка алгоритмов на тестовых задачах (benchmarks) данной проблемной области. К сожалению, в настоящее время не существует согласованного каталога таких задач для оценки старых или новых алгоритмов решения, хотя для многих типовых задач они уже сложились и широко используются.